ФизЭлектроника PDF-лекции / (Лекция 6)

Движение заряженных частиц в электрических и магнитных полях.

Настоящий раздел посвящен рассмотрению движения заряженных частиц в электрических и магнитных полях в вакууме с использованием наиболее распространенных способов описания такого движения.

Часть пространства, в котором движутся частицы, представляет собой сосуд, в котором степень разряжения составляет 10-4 – 10 -6 торр (средний вакуум). Гравитационной силой, действующей наряду с электрическими и магнитными силами, можно пренебречь, т.к. она намного порядков меньше последних.

Движение заряженных частиц может быть описано различными способами, но наиболее распространенной является ньютонова форма уравнений движения. Наряду с этим при анализе электронно-оптических систем в ряде случаев оказывается целесообразным применение уравнений в форме Лагранжа и Гамильтона.

Уравнения движения в форме Ньютона.

На заряженную частицу, движущуюся в электрическом и магнитном поле,

R	× B ) С учетом этого уравнения
действует сила Лоренца: F = eE + e( v

движения заряженной частицы в векторной форме будут иметь вид:

R R R R

m dv dt = eE + e( v × B ) .

Первый член правой части этого уравнения представляет собой силу, действующую на частицу со стороны электрического поля, а второй – силу, обусловленную магнитным полем, причем последняя, как нетрудно видеть, зависит от индукции магнитного поля и скорости частицы. Проектируя векторное уравнение на оси координатной системы, получаем эквивалентную ему систему скалярных уравнений, вид которых зависит от выбора координат системы.

В декартовых координатах x, y, z:

m&x& = eE		+ ey&B − ez&B			y (1.1)
	x		z
m&y& = eEy + ez&Bx − ex&Bz
m&z& = eE	z	+ ex&B	y	− ey&B
					x

В цилиндрических координатах r, θ, z:

			&				2		&
m(&r& − rΘ								) = eEr + e(rΘBz
								.
		1 d				2		∙	&
m					(r
								Θ) = eEΘ + e(zBr
		r dt
	&&		= eEz					&	&	)
mz							+ e(rBΘ − rΘBr

− z&BΘ )

(1.2)

− r&Bz )

Закон сохранения энергии.

Используя уравнение Лоренца, получим закон сохранения энергии для частицы, движущейся в стационарных электрическом и магнитном полях. Умножая левую и правую части на v , имеем:

R

R R

R dv

R

R

R

mv

= evE + ev( v

× B )

(1.3)

dt

R

R

R dv

=

d v 2

R R

× B ) = 0 ; E = −gradU .

Т.к. v

; v( v

dt

dt 2

Получим:

R

2

dU

d mv

R

= −evgradU = −e

dt

2

dt

Откуда:

R2

mv + eU = const (1.4) 2

Это уравнение утверждает, что полная энергия (Е) частицы, равная сумме

	R	2
кинетической энергии T =	mv		и потенциальной энергии V = eU , остается
2

неизменной при движении частицы в стационарных электрическом и магнитном полях.

Уравнение (1.4) может быть представлено в эквивалентном виде:

R	2		R	2
mv		−	mvн		= −e(U −U		) (1.5)
						н
2		2

R

Где vн и Uн - значения скорости и потенциала в некоторой начальной точке. Отсюда следует, что изменение кинетической энергии частицы при ее движении равно взятому с обратным знаком изменению потенциальной энергии.

Для случая, когда частицы эмитируются с нулевыми начальными скоростями источником, имеющим нулевой потенциал:

R 2

mv = −eU 2

Т.к. левая часть этого выражения есть положительная величина, то частицы могут достигать только тех точек поля, где − eU > 0 .

С учетом этого:

R	2
mv
		=		eU		и v =	2		( eU )		m
2

Уравнения движения Лагранжа.

В обобщенно криволинейных координатах qi уравнение имеет вид:

	d		∂L		−	∂L	= 0 i=1,2,3…(1.6)
			&			∂qi
	dt		∂qi

где L- функция Лагранжа.

В случае чисто электростатических полей:

	m	2	&2	2
L = T −V =		∑hi		− eU , hi	- коэффициент Ламэ (1.7)
	2		qi
		i

При движении частицы в магнитных и комбинированных магнитных и электростатических полях:

					R
L = T −V + e( AV ) (1.8)
где A - векторный магнитный потенциал;
	m	2			&2			2	&2
L =		∑hi
	2			qi − eU( qi ) + e∑Ai hi					qi (1.9)
		i				i
Уравнения движения Гамильтона.
Функция Гамильтона:						∂L
		&	2		− L , где pi =			- обобщённый импульс
H = ∑ pi qi							&
	i
							∂qi

t

Выразив действие S = ∫L( qi q&i )dt через эту функцию и применив принцип наименьшего

t0

действия, можно получить уравнения движения в форме Гамильтона:

&	= −	∂H	&	= −	∂H
pi		∂qi	; qi		(1.10)
					∂pi

Нетрудно показать, что функция Н числено равна полной энергии частицы Е,

.

Это позволяет построить функцию Гамильтона, исходя из полной энергии Е, если выразить последнюю через обобщенные координаты и обобщенные импульсы.

Для комбинированных электрических и магнитных полей полная энергия выражается:

	m	2	&2
E = T +V =		∑hi		− eU( qi ) (1.11)
	2		qi
		i

Уравнения Лагранжа и Гамильтона для акс-симметр. полей.

Уравнения получаются из приведенных выше общих уравнений, если в них подставить следующие значения обобщенных координат, импульсов, коэффициентов Ламэ и составляющих векторного магнитного потенциала:

q1 = r

h1 =

&

&

=pr

A1 = Ar = 0

1 q1

= r p1

q2 =Θ

h2 = r q2

=Θ p2 =pΘ

A2 = AΘ = 0

&

&

q3 = z

h3 =

&

= z&

p3 =pz

A3 = Az = 0

1 q3

d

∂L

∂L

d ∂L

∂L

−

= 0 ;

−

= 0 ; + (1.20)

∂r

&

∂Θ

dt

∂r

dt

∂Θ

&

L = m [r&2 + r 2Θ& 2 + z&2 ]+ erΘ&A − eU( r ,z )

2

&

= −

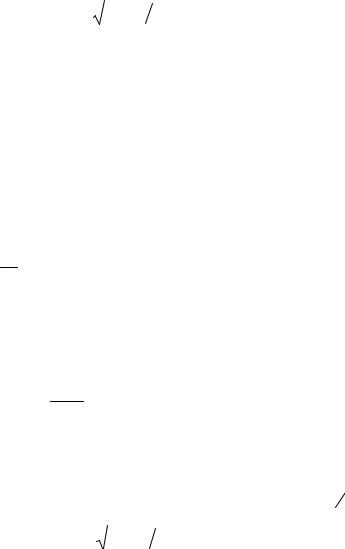
∂H

&

= −

∂H

&

= −

∂H

;

pr

∂r

; pΘ

∂Θ

; pz

∂z

∂H

∂H

∂H

&

r& =

∂pr

;Θ =

∂pΘ

; z& =

∂pz

;

(1.21)

1

p2

1

H =

+

( p − erA )2 + p2

+ eU( r ,z )

2

r

r

Θ

z

2m

Движение при больших скоростях

Одним из следствий СТО является зависимость массы частицы от скорости её движения:

m = m( v ) =			m0			= γm0
			− v2
1				c2

Эта формула и получаемая отсюда связь массы и энергии следуют из СТО, построенной на основе общих фундаментальных соображений.

Масса каждого материального объекта, движущегося со скоростью V, зависит в соответствии с приведенным выше соотношением от скорости. Т.о., масса увеличивается при увеличении скорости и стремится к бесконечности, когда скорость стремится к скорости света с.

Из сказанного выше следует, что второй закон Ньютона справедлив лишь в первоначальной формулировке, данной Ньютоном:

d R = R

( mv ) F

dt

Подсчитаем работу, совершенную силовым полем по перемещению частицы на участке траектории dr. Справедливо равенство:

Fv = v dmv dt

Производя дифференцирование, находим:

dmv

d

m0v

d

2

v2

− 12

d 2

v

dt

= v

dt

1 − v

2

c

2 =

m0c 1 −

c

2

= mc

dt

dt

Отсюда следует равенство:

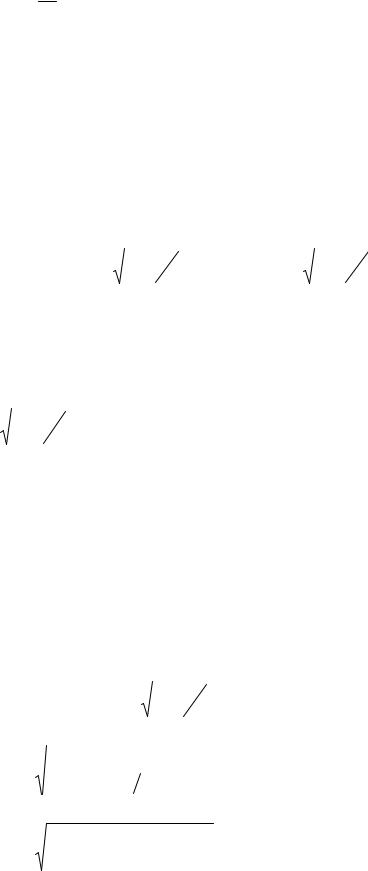
Fv = d mc2 dt

интегрирование обеих частей которого приводит к формуле:

Wk = mc2 - m0c2

Это соотношение интерпретируется как общее положение: любой системе с массой m соответствует энергия mc2, т.е.:

W = mc2

Масса покоя m0 соответствует энергии m0c2. При увеличении скорости увеличивается энергия, что как раз и проявляется в форме возрастания массы. Т.о. прирост энергии может быть выражен в виде:

		m0c	2					2	2			1
Wk = W -W0 =							- m0c		= m0 c							- 1
		1 - v2										1 - v2
				c	2								c	2

Полученное выражение дает точное значение кинетической энергии. Если

v<<c, то, используя известное разложение в ряд:

( 1 + x )α » 1 + αx

Получаем:

1

» 1 +

1

v2

+ ...

2 c2

1 - v2

2

c

Откуда:

2

1 v2

m v2

Wk » m0c

1

+

- 1

=

0

2

2 c2

В случае малых скоростей мы приходим снова к классическому выражению для кинетической энергии.

Используя закон сохранения энергии, можно определить скорость, которую приобретает частица, ускоряемая разностью потенциалов U. Потенциальная энергия qU в этом случае идет на приращение массы частицы.

2		2			m c2				2
mc - m0c = qU ;				0						- m0 c = qU
					1 - v2			2
							c
Отсюда можно получить:
v = c	1 -		1
		( 1	+ qU	m0c2 )2

Конкретно для электрона эта формула перепишется в форме:

v = c 1 -			1
		+ 1,96	×10−6 U )2
( 1

Из двух последних соотношений следует, что при безграничном увеличении напряжения скорость растет не до бесконечности, а асимптотически приближается к скорости с. Если значения U малы, то полученная формула

при условии, что можно удовлетвориться первым членом разложения в ряд по степеням qU/m0c2, переходят в прежнее выражение:

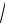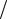v = 2qU m

Нетрудно ответить на вопрос, каковы границы применимости классических формул, т.е. до каких пор можно не учитывать увеличение массы, принимать её в уравнениях за постоянную величину и выносить за знак дифференциала. Пусть приращение энергии частицы под действием силового поля выражается в виде:

Wk = mc2 - m0c2

Деля это равенство на m0c2, получаем:

	Wk	=	m	- 1 =	m − m0	= m
	m c2		m		m
						m
0		0		0		0
где ∆m – приращение массы.

Т.к. m0c2=W0 – энергия покоя, то m = Wk

m0 W0

Это означает, что фактором приращения массы пренебрегают до тех пор, пока прирост энергии можно не учитывать по сравнению с энергией покоя. Отсюда следует, что чем меньше масса покоя частицы, тем при меньших энергиях необходимо учитывать релятивистские поправки; наиболее чувствительным к изменению массы покоя является электрон.

Пример:

Энергия покоя электрона

W0 e = mec2 = 9,1 ×10−31( 3 ×108 )2 = 8,19 ×10−14 Вт× с = 511 ×105 eV . Это означает,

что при прохождении электроном разности потенциалов 500000В его масса увеличивается.

Энергия покоя протона превышает энергию покоя электрона пропорционально соотношению их масс:

W	=	mp	0,511 = 938,3MeV
0 p		me

Масса протона в большинстве физических опытов может рассматриваться как постоянная, а масса электрона с энергией в 10000eV почти на 2% превышает массу покоя.

Для фотона: Энергии hv соответствует масса, определяемая соотношением hν = mc2 . Отсюда масса движущегося со скоростью света фотона равна

m = hν . Эта масса может иметь конечное значение лишь при условии, что c2

масса покоя фотона равна нулю.

Полезным также оказывается выражение энергии mc2 как функции импульса p=mv:

W = mc2 = m02c4 + p2c2

Скорость также может быть выражена через импульс и энергию: v = pc2 W

Используя полученные выражения, можно выразить скорость релятивистской частицы через ускоряющий потенциал:

						γ + 1 12
	v =	( eU )					1
		2
			m0				γ
						2

Где γ = 1 + eU m0 c2

Для электрона v = 5,95 ×10	7				γ + 1 12	1	; γ	= 1 + 1,96 ×10	−6	U , где v − см / с;
		U
						γ
					2

U − Вольт.

Уравнения движения в аксиально-симметричных электрическом и магнитном полях.

Для описания движения используются цилиндрические координаты. Предполагается, что скалярный и векторный потенциал не зависят от

азимутальной координаты θ, т.е.: ¶∂ΘU = 0 ; ¶∂ΘA = 0

Уравнения движения в цилиндрической системе координат могут быть получены из уравнения Лагранжа (1.6):

d

¶L

¶L

-

= 0 i=1,2,3…

¶qi

&

dt ¶qi

И релятивистской функции Лагранжа (**):

2

1 2 2

2

2

12

&

&

L = -m0c 1 -

c

2

( r& + r Θ

+ z&

) - eU + e( r&Ar + rΘA + z&Az

)

Подставляем в исходное уравнение проекции на координатные оси:

d

2

r

e

¶U

γm0

¶U

¶U

&

&

& 2

r

2

= -

- Bz rΘ

-

rΘ

+ BΘ z& )

- r&

¶r

+ z&

2

dt

γm0 ¶r

e

¶z c

d 2 z

e ¶U

&

¶U

¶U z&

2

= -

- Br rΘ

- BΘ r& - r&

¶r

+ z&

2

dt

γm0 ¶z

¶z c

2

&

2 &

e

r

Θ

- r0

Θ0

= -

( rAΘ

- r0 AΘ 0 )

γm

0

2

&

- начальный угловой момент; AΘ 0 - азимутальная компонента векторного

r0 Θ0

потенциала в начальной точке, имеющей радиальную координату - r0 .

В случае интенсивных электронных пучков электрическое и магнитное поля, входящие в уравнение, должны вычисляться с учетом собственных полей пучков.

4.2.Движение потоков заряженных частиц

Вряде современных электронных приборов используются направленные управляемые потоки (пучки) электронов, создаваемые с помощью магнитных и электрических полей. Под пучком заряженных частиц обычно понимают поток частиц, движущихся в одном направлении примерно параллельно друг другу: разброс по энергиям и отношение поперечной скорости к продольной составляют не более нескольких процентов. Обычно рассматривают распространение пучка в вакууме (10-5 – 10 -3 Па). Объемный заряд пучка может оказаться сильнейшим фактором, влияющим на свойства пучка. В

пучке частиц одного вида могут присутствовать и другие частицы,

взаимодействующие с ним. Если взаимодействие становится столь значительным, что частицы пучка приобретают поперечную скорость, то утрачивается основной признак пучка. Особенно быстро это проявляется в среде с повышенным давлением, хотя ограниченное расстояние пучок может проходить и в плотных средах.

Во всех случаях движение заряженных частиц происходит под действием электрических и магнитных полей. Следовательно, полное описание поведения пучка может быть получено из уравнений движения и известного распределения полей.

Примеры (Аксиально-симметричные поля).

Широко распространенными типами электрических и магнитных полей, используемых в технике пучков, являются аксиально-симметричные поля, анализ движения в которых проводят в цилиндрических координатах

( r,Θ, z ).

Ур-ия Ньютона

Исходные уравнения:

&

2

&

− z&BΘ )

m(&r& − rΘ

) = eEr + e(rΘBz

.

1 d

2

∙

&

&

m

(r

)

Θ) = eEΘ + e(zBr

− rBz

r dt

&&

= eEz

&

&

)

mz

+ e(rBΘ − rΘBr

Тогда в условиях аксиальной симметрии с учетов свойств полей( EΘ = BΘ = 0 ) :

					& 2			&
	m( r&& − rΘ						) = eEr + erΘBz
		1 d					&		(1.12), (1.13), (1.14),
					2
	m				( r	Θ ) = e( z&Br		− r&Bz	)
		r dt
	&&						&
	mz = eEz					− rΘBr

Эти уравнения получаются из общих уравнений движения, записанных в цилиндр. координатах, если в них положить равным нулю азимутальные компоненты EΘ = BΘ = 0 .

В случае акс.сим. поля векторный магнитный потенциал в точке с корд. r, z

может быть выражен через поток магнитного поля, сцепленный с контуром радиуса

A( r ,z ) =Ψ 2πr

Движение в аксиальном и радиальном направлениях приводит к изменению магнитного потока, пронизывающего траекторию частицы (рис. 4.3б). Если в качестве начальной точки траектории взята точка, лежащая на катоде, то Ψн имеет смысл магнитного потока Ψк , сцепленного с круговым

контуром радиуса rk.

r

аксиально-симметричное магнитное поле

rк

z

				r			× 2πrdr, из уравнений движения можно
Вводя магнитный поток Y = ∫ Bz
				0
		2	&	e
получить соотношение	r		Θ +	2π m		Ψ = const,		известное как теорема Буша.

Она связывает угловую скорость частицы с магнитным потоком,

пронизывающим ее траекторию (рис. 4.3а).

Теорема Буша

Выразим входящие в (1.13) компоненты магнитного поля Br и Bz через

r

магнитный поток Ψ = ∫Bz × 2πrdr :

0

B = -

1

∂Ψ , B = −

1

∂Ψ .

r

2πr

¶z

z

2πr ∂r

Имеем:

d 2

= -

e

¶Ψ

+ r&

¶Ψ

( r Θ& )

z&

¶z

¶r

dt

2πm

Откуда:

r 2Θ& +

e

Ψ = const

(1.15)

2πm

Либо:

		= -	e	¶Ψ
				¶t
			2πm

	r 2Θ& - r 2Θ& - =	e	(Ψ -Ψ ), где «н» - начальные условия. 1.15’
		2πm
	н н		н

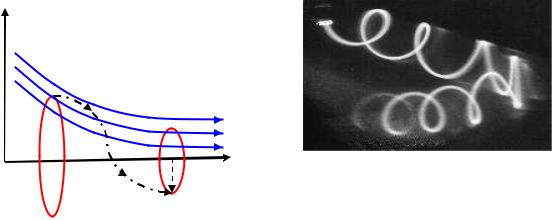
Это выражение – теорема Буша. Оно утверждает, что изменение углового момента частицы, движущейся в аксиально-симметр. полях, определяется только изменением магнитных потоков, сцепленных с круговыми контурами, радиусы которых соответственно равны текущей и начальной радиальным координатам частицы (см. рис.).

r

аксиально-симметричное магнитное поле

rк

Отражение сильноточного электронного

z

пучка магнитным зеркалом

а

б