теория автоматов / automat-p1

деленным, а в качестве состояния δ 1(cm, zk) будет приниматься любой из финальных классов ci (их может быть несколько), содержащий все определенные состояния вида δ (av, zk)(av cm). Очевидно, финальные классы ci с требуемыми свойствами всегда существуют.

За начальное состояние автомата Ñ можно принять любой финальный класс, содержащий начальное состояние автомата A, либо принять за начальные состояния автомата Ñ некоторые или все финальные классы, содержащие начальное состояние автомата A.

Совокупность E всех финальных классов автомата A удовлетворяет условию полноты и условию замкнутости. Первое условие означает, что каждое состояние автомата A принадлежит какому-либо из финальных классов. Второе условие означает, что для каждой буквы входного алфавита все состояния каждого финального класса (с точностью до неопределенных переходов) переходят в состояния, принадлежащие одному финальному классу (тому же самому или другому). Пусть E0 – наименьшее подмножество E, удовлетворяющее условиям полноты и замкнутости. Условие замкнутости здесь означает, что для каждой буквы входного алфавита все состояния каждого финального класса из E0 (с точностью до неопределенных переходов) переходят в состояния, принадлежащие одному (тому же самому или другому) финальному классу из E0. Назовем минимальной нормальной формой автомата A нормальную форму, построенную по множеству финальных классов E0.

Если в минимальной нормальной форме Ñ связного автомата A в качестве начального состояния выбран какой-либо финальный класс, содержащий начальное состояние автомата A, то автомат Ñ будет иметь наименьшее число состояний среди всех автоматов, эквивалентно продолжающих автомат A.

Процесс минимизации автомата A можно разбить на два этапа. На первом этапе с помощью какого-либо эвристического приема строится эквивалентный автомату A автомат B с меньшим, чем у A количеством состояний, а на втором этапе стандартным методом осуществляется минимизация автомата A. При этом чем меньше количество состояний имеет автомат B, тем проще будет его последующая минимизация.

Наибольший объем работы по минимизации автомата связан с нахождением финальных классов. Для конечных автоматов эта работа может быть существенно упрощена с помощью треугольных таблиц. Правила составления и использования этих таблиц удобнее всего рассмотреть на конкретных примерах абстрактного синтеза автоматов.

51

5.5. Пример минимизации автомата Мили

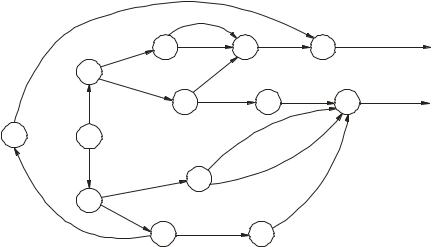
Пусть частичный автомат Мили A задан графом, приведенным на рис. 5.1. Это связный автомат без неопределенных выходных сигналов. Его минимизацию будем осуществлять в два этапа. Сначала построим эквивалентный автомату A автомат B с меньшим чем у A числом состояний.

Согласно рис. 5.1, единственным применимым к состояниям a4, a6, a9 è a18 входным словом будет однобуквенное слово p = α с результатом применения q = w0. По этой причине состояния a4, a6, a9 è a18 совместимы, и их можно заменить одним состоянием b4. Точно так же убедимся в совместимости состояний a11, a14, a15 è a20, в силу чего их можно заменить одним состоянием b7. Для состояний a3, a5, a8 применимыми входными словами будут лишь двухбуквенное слово p1= αα , которому соответствует результат применения q1= w0w0, и однобуквенное слово p = α с результатом применения q = w0. Следовательно, состояния a3, a5, a8 совместимы, и их можно заменить одним состоянием b3. Переобозначив теперь на рис. 5.1 a0 íà b0, a1 íà b1, a2 íà b2, a7 íà b5,

a10 íà b6, a12 íà b8, a13 íà b9, a16 íà b10, a17 íà b11 è a19 íà b12, получим граф автомата Мили B, изображенный на рис. 5.9.

	b 1
	z 0 / β
b 11	b 0
	z 1 / β
	b 8
z	/
1
	w
	0

α / w 0

z 0 / w 1

/β

b

z

1 / w 0

b

α

/ w 0

b

α / w

0

b 0

2

3

4

z0

z

w

1

/ β

/

1

z0

z 1

/ w 0

α / w 1

α / w 1

b 5

b

b

b 0

6

7

w

0

/

z0

w

/

1

z1

z

w 0

b

9

/

0

w

0

/

z

β

α

1

/

b 10

z

/ w

1

b 1 2

1

Ðèñ. 5.9

52

Автомат B имеет только 13 состояний вместо 21 состояния у автомата A. Эти автоматы эквивалентны. Действительно, пройдя все пути из состояния b0 через другие состояния опять в b0, убедимся в том, что оператор автомата B определен на всех входных словах из табл. 5.3 и на их начальных отрезках.

Других слов область определения оператора Â не содержит. При этом каждому входному слову оператор автомата B сопоставляет то же самое единственное выходное слово, что и оператор автомата A.

Таблица 5.12

b t`	α	z	z
b	–	b /β	b&/β
b	–	b /β	b#/β
b	–	b!/w	b!/w
b!	b"/w	–	–
b"	b /w	–	–
b#	–	b!/w1	b$/w
b$	b%/w	–	–
b%	b /w	–	–
b&	–	b'/w	b /β
b'	–	b%/w	b%/w
b	–	b /w	b /w
b	b"/w	–	–
b	b%/w	–	–

Графу рис. 5.9 соответствует таблица переходов-выходов табл. 5.12 автомата B. Финальные классы этого автомата будем искать с помощью треугольной таблицы (табл. 5.13), которая строится следующим образом.

Строки обозначаются состояниями b1, b2, ..., bh–1, а столбцы состояниями b0, b1, ..., bh–2, ãäå h – число состояний автомата. На пересечении i-й строки и j-го столбца записываются условия, при которых возможно совмещение состояний bi è bj. Если состояния нельзя совместить ни при каких условиях, ставится знак , если совмещаются безусловно, то знак . Клетки, соответствующие пересечениям строк и столбцов с одинаковыми индексами, не заполняются. Окончательное совмещение со-

53

стояний определяется на основании анализа непротиворечивости условий, записанных в клетках. Для рассматриваемого примера треугольная таблица (табл. 5.13) строится следующим образом.

Согласно табл. 5.12, состояниям b0 è b1 для каждого входного сигнала соответствуют одинаковые выходные сигналы, поэтому состояния b0 è b1 можно совместить, если при каждом входном сигнале они переходят в совместимые состояния, т. е. если можно совместить состояние b1 ñ b2 и состояние b8 ñ b5. Эти условия и записываются в верхнюю клетку, соответствующую столбцу для b0 (табл. 5.13). Поскольку для состояний b0 è b2 найдется входной сигнал, для которого (см. табл. 5.12) выдаются различные входные сигналы, эти состояния совместить невозможно, и соответствующая клетка табл. 5.13 отмечается символом Ч. Состояния b0 è b3 совмещаются безусловно, поскольку при каждом входном сигнале переход определен только для одного из них. В соответствующей клетке табл. 5.13 нужно поставить поэтому символ. Затем анализируются остальные пары состояний столбца табл. 5.13, отмеченного состоянием b0, после чего точно так же анализируются пары состояний, соответствующие остальным столбцам, начиная с верхней строки в каждом столбце. В результате этого анализа все клетки табл. 5.13 окажутся заполненными символами Ч , или условиями, при которых возможно совмещение состояний, соответствующих клеткам. После этого начинается анализ условий, записанных в клетках табл. 5.13.

Состояния b0 è b1 можно совместить в том случае, если совместимы состояния b1, b2 è b5, b8. Но в клетке, соответствующей состояниям b1, b2, стоит знакЧ , поэтому совместить состояния b0 è b1 невозможно и в соответствующей им клетке ставится символ Ч . Аналогичным образом находим, что и в клетке, отмеченной состояниями b2, b4, нужно поставить знак Ч . В клетке, отмеченной состояниями b0 è b4, стоит символ , поэтому в клетке, отмеченной состояниями b3 è b4, так же нужно поставить . В результате после такого анализа клеток, в которых записаны условия совместимости, в каждой клетке табл. 5.13 будет стоять символ Ч или символ . По такой треугольной таблице можно найти финальные классы.

Процедура нахождения минимального множества финальных классов, предполагающая полный перебор совместимых состояний, приведена в литературе [5]. Поскольку часто эта процедура оказывается гро-

54

Таблица 5.13

b , b

b

b , b

#

&

b

b!

b

b , b"

"

b#

b$

b%

b&

b'

b

b%, b

b%, b

b

b", b%

b , b"

b

b", b%

b

b

b

b!

b"

b#

b$

b%

b&

b'

b

b

моздкой, рассмотрим упрощенный способ формирования множества финальных классов. Этот способ, к сожалению, не гарантирует получе- ние оптимального результата в случае частичного автомата с большим числом состояний, так как содержит элементы альтернативного неформального выбора при доопределении автомата и в процессе включения

55

конкретных состояний в финальные классы. Предлагаемый способ может быть описан с помощью следующей процедуры.

1. Формируется множество пар совместимых состояний на основании разметки каждого столбца треугольной таблицы.

Для рассматриваемого автомата Мили (табл. 5.12) по табл. 5.13 находим следующие пары совместимых состояний:

(b	0	, b ),	(b , b ),			(b , b ),			(b , b ),			(b , b ),
		3	1	3		2	3		3	4			4		5
(b	0	, b ),	(b , b ),			(b , b ),			(b , b ),			(b , b ),
		4	1	4		2	4		3	5			4		8
(b	0	, b ),	(b , b ),			(b , b ),			(b , b ),			(b , b ),
		6	1	6		2	6		3	8			4		9
(b	0	, b ),	(b , b ),			(b , b ),			(b , b ),			(b , b			10		),
		7	1	7		2	7		3	9			4
(b0, b11),			(b1, b11),			(b2, b11),			(b3, b10),			(b4, b12),
(b0, b12),			(b1, b12),			(b2, b12),
(b	6	, b ),	(b , b ),			(b , b	11	),	(b , b	11	),	(b	10	, b		11		),
		7	7	8		8			9
(b	6	, b ),	(b , b ),			(b , b	12	),	(b , b	12	),	(b	10	, b		12		).
		8	7	9		8			9
(b	6	, b ),	(b , b	10	),
		9	7
(b6, b10),			(b7, b11),

(b5, b6), (b5, b7), (b5, b11), (b5, b12),

2. На основе полученного множества производится укрупнение групп совместимых состояний, в результате чего должна быть получена полная совокупность финальных классов, в каждом из которых все состояния совместимы между собой. Для уменьшения сложности этой процедуры возможно при формировании каждого очередного класса совместимых состояний не рассматривать состояния, уже вошедшие в какой-либо из сформированных классов. В частности, в рассматриваемом случае состояние b0 совместимо с состояниями b3 è b4, причем состояние b3 так же совместимо с состоянием b4, следовательно, их можно включить в один финальный класс K1. Состояние b0 совместимо и с состоянием b6, однако b6 не совместимо с состоянием b3 и не может входить в этот же финальный класс. Аналогичная ситуация обнаруживается при анализе совместимых с b0 состояний b7, b11, b12. Подобным же образом формируются и все остальные финальные классы. В результате будут получены следующие классы совместимых состояний:

K1 = {b0, b3, b4}, K2 = {b1, b6, b7}, K3 = {b2, b11}, K4 = {b5, b12},

K5 = {b8}, K6 = {b9}, K7 = {b10}.

56

3. Производится анализ полученных финальных классов на удовлетворение условиям полноты и замкнутости. Проверка условия полноты очевидна и не вызывает затруднений, а проверка условия замкнутости выполняется по таблице переходов-выходов для всех состояний автомата. Если какие-либо два состояния, входящие в один из выбранных финальных классов, переводятся некоторым входным сигналом в состояния, принадлежащие разным классам, то нужно выбрать новое решение и проверить его на замкнутость.

Для рассматриваемого автомата при проверке финальных классов на замкнутость оказывается, что принадлежащие классу K2 состояния b6 è b7 сигналом a переводятся в состояния, принадлежащие разным классам (b6 –a→ b7 K1, à b7 –a→ b0 K2), т. е. условие замкнутости не выполняется. Следовательно, необходимо одно из этих состояний (например, b7) перенести в другой класс, не нарушая при этом условие замкнутости. Таким классом может быть класс K5. В результате будет получено окончательное множество финальных классов, совпадающих с состояниями минимизированного автомата C

c0 = K1 = {b0, b3, b4},	c3 = K4 = {b5, b12}, c6 = K7 = {b10}.
c1 = K2 = {b1, b6},	c4 = K5 = {b7, b8},
c0 = K3 = {b2, b11},	c5 = K6 = {b9}.

4. Строится таблица переходов-выходов минимизированной нормальной формы заданного автомата. Далее по этой таблице можно построить граф переходов минимизированного автомата. Состояния переходов и выходные сигналы в этом автомате определяются по переходам и выходным сигналам того состояния, которое наиболее полно определено.

			Таблица 5.14
c t–	α	z		z
c	c /w	c /β		c" /β
c	c" /w	c /β		c! /β
c	c /w	c /w		c0 /w
c!	c" /w	c /w		c /w
c"	c0 /w	c# /w		c$ /β
c#	–	c" /w		c" /w
c$	–	c /w		c! /w

57

w	1
α

c 0 w 0

w 1

w	1

w 0

z0

w 1 z1

						z1
	z0	z 1		β
	c 1		z1 c 2 w 1
β		w 0
	α				α	z0
	w 1	w
β		0
		z0	w 0
α	c 4				c 5
		w 0	z	0
	z 1				z1
		w 1
		Ðèñ. 5.10

α	z	0
β		c	2	w 0

z 1

c	z0
	6

β

В рассматриваемом примере получены таблица переходов-вы- ходов минимизированного автомата (табл. 5.14) и граф переходов (рис. 5.10).

5.6. Пример минимизации автомата Мура

Пусть частичный автомат Мура A задан графом, представленным на рис. 5.2. Поскольку все состояния этого автомата достижимы, а выходные сигналы определены для всех состояний, отпадает необходимость исключать недостижимые состояния. Будем опять минимизировать автомат в два этапа. Сначала построим эквивалентный автомату A автомат B с меньшим числом состояний.

Согласно рис. 5.2, если автомат A установлен в любое из состояний a4, a6, a9, то единственным допустимым входным словом будет однобуквенное слово p = α , которому соответствует единственное однобуквенное слово p = 0. По этой причине состояния a4, a6, a9 совместимы и их можно заменить одним состоянием b4. Аналогичным образом находим, что совместимы состояния a11 è a15, a14 è a20.

Первую пару заменим состоянием b8, вторую – состоянием b13. Если автомат установлен в состояния a3 è a8, то допустимыми вход-

58

ными словами будут лишь двухбуквенное слово p1= αα , которому соответствует выходное слово q1= w0w0 и однобуквенное слово p = α , которому соответствует выходное слово q = w0. Следовательно, состояния a3 è a8 совместимы, и их можно заменить одним состоянием. Переобозначив теперь на рис. 5.2 a0" íà b0", a0' íà b0', a1 íà b1, a2 íà b2, a5 íà

b5, a7 íà b6, a10 íà b7, a11 íà b8, a12 íà b9, a13 íà b10, a16 íà b11, a19 íà b12, a20

íà b13, a17 íà b14, a18 íà b15, получим граф автомата Мура B, изображенный на рис. 5.11.

Автомат B имеет 17 состояний вместо 22 у автомата A и эти автоматы эквивалентны.

a 3

z 1

w1

α

b 2

β

a 5

α

b ´

z 0

w0

z 0

α

0

b3w1

b0´

z0

β

z

1

b 6

z 0

z

w0

z1

β

1

b 7

α

b8

α

b´´0

z0

z 1

w0

w0

z

b10

b ´´

z

1

0

z0

0

w1

β

z1

w0

z1

b12

α

b13

α

b´´0

b 11β

w1

w0

z0

b14

α

b15

α

b ´

w0

w1

0

Ðèñ. 5.11

Действительно, пройдя все пути из начальных состояний через другие состояния опять в начальные, убеждаемся в том, что оператор автомата определен на всех входных словах из табл. 5.3 и на начальных отрезках и только на них. При этом каждому входному слову он сопоставляет то же самое единственное выходное слово, что и оператор автомата A.

Графу рис. 5.11 соответствует отмеченная таблица переходов (табл. 5.15) автомата B. Финальные классы автомата B будем находить с помощью треугольной таблицы (табл. 5.16), которая заполняется так же, как и для автомата Мили. Финальные классы находятся из нее для автомата Мура по тем же правилам, что и автомата Мили.

59

				Таблица 5.15
w t–	b t–	α	z		z
w	b	–	b		b'
w	b	–	b		b'
β	b	–	b		b$
β	b	–	b3		b#
w	b!	b"	–		–
w	b"	b	–		–
w	b#	b"	–		–
β	b$	–	b!		b%
w	b%	b&	–		–
w	b&	b	–		–
β	b'	–	b		b
w	b	–	b!		b&
β	b	–	b"		b
w	b	b!	–		–
w	b!	b	–		–
w	b"	b#	–		–
w	b#	b	–		–

Из табл. 5.16 имеем следующие пары совместимых состояний:

(b	0	', b ),	(b ", b ),			(b , b	15	),	(b , b ),			(b , b	10	),
		4	0	3		3			4	5		5
(b	0	', b ),	(b ", b ),						(b , b	10	),
		5	0	8					4
(b	0	', b ),	(b ", b	12	),
		7	0
(b0', b13),			(b0", b15),
(b0', b14),
(b7, b10),			(b10, b13),			(b13, b14).
(b7, b13),			(b10, b14),

После проведения укрупнения групп совместимых состояний полу- чим финальные классы и соответствующие им состояния минимально-

го автомата C.
C0' = K1 = {b0', b4, b5},	C5 = K7 = {b8},
C0'’ = K2 = {b0'’, b3, b15},	C6 = K8 = {b9},

60