теория автоматов / aut_langs-nn

	q1	a,c	с
a	b	q0	b
b,с	a		q1
			a,b
q0		q2
	с
b		a,c
		Рис. 3.9

Пример 3.4.

Построить недетерминированный конечный автомат, распознающий множество чисел, делящихся на 25.

4. Замкнутость класса регулярных языков относительно операций конкатенации, возведения в степень и итерации.

Пусть L1 и L2 – регулярные языки, распознаваемые детерминированными конечными автоматами К1={Q1, A, q10, g1, F1} и К2={Q2, A, q20, g2, F2} соответственно. Дадим алгоритм синтеза по имеющимся диаграммам переходов конечных автоматов К1 и К2 диаграммы переходов недетерминированного конечного автомата К, распознающего язык L1L2 ,т.е. конкатенацию (сцепку) языков L1 и L2.

Сначала предположим, что q10 F1; выполнение данного условия будем именовать общим случаем. Через М обозначим совокупность тех дуг (вместе с надписанными над ними буквами) в диаграмме переходов автомата К1, которые своими концами имеют вершины подмножества F1. Специально отметим, что (в случае их присутствия в диаграмме автомата К1) в М входят и петли, т.е. дуги вида (q1j, q1j), где q1j F1. Для каждой принадлежащей множеству М дуги (q1i,q1j) с надписанной над ней буквой х входного алфавита строим дугу-дубликат (q1i,q20) с той же надписанной буквой. Так реализуется «сцепка» диаграмм переходов конечных автоматов К1 и К2, результатом которой является диаграмма переходов конструируемого недетерминированного конечного автомата К; начальным состоянием автомата К объявляется состояние q10, совокупность F «хороших» состояний автомата К считается совпадающей с F2. Согласно выполненному построению, до перехода по некоторой дуге-дубликату в состояние q20, конечный автомат К функционирует как автомат К1, после перехода в q20 и до завершения работы – как К2.

Сконструированный конечный автомат проверяет, можно ли входное слово

α, α А*, разбить на две последовательные части α1 и α2 так, что α1 L1 и α2 L2 (указанное разбиение оказывается возможным тогда и только тогда, когда существует способ работы данного автомата такой, что, обработав тестируемое слово α, автомат оказывается в состоянии из F).

Действительно, конечный автомат К, начиная работу из состояния q01,

начальную часть произвольного входного слова α обрабатывает в режиме автомата К1. Пусть на некотором такте работы автомата K в данном режиме поступила буква х. Предположение о том, что она является последней в

принадлежащей L1 части α1 входного слова α, возникает тогда, когда под воздействием х автомат К1 может перейти в свое «хорошее» состояние. На данном такте для недетерминированного автомата К по его построению имеем две возможности:

1)выполнить переход в соответствии с диаграммой автомата К1 (при этом считается, что данной буквой х начальная часть α1, α1 L1, входного слова не заканчивается);

2)под воздействием х по соответствующей дуге-дубликату перейти в состояние q20 (здесь считается, что буквой х завершается первая часть α1, α1 L1,

входного слова α). Далее автомат К будет функционировать как автомат К2; его работа должна завершиться в состоянии, принадлежащем подмножеству

F2, если оставшаяся часть α2 тестируемого слова α принадлежит языку L2. За счет своей недетерминированности, автомат К может по-разному

разбивать входное слово α на части α1, α1 L1, и α2. Слово α принадлежит языку, распознаваемому автоматом К тогда и только тогда, когда его можно представить в виде α=α1α2, где α1 L1 и α2 L2; отметим, что из условия q10 F1 следует α1≠λ.

Первым специальным случаем назовем следующую ситуацию: q10 F1 и q20 F2. Специфика ситуации заключается в том, что в язык L1 входит и пустое слово. В силу возможного равенства α1=λ, следует конструировать автомат К таким образом, чтобы для любой буквы х входного алфавита А имелась дополнительная возможность перехода автомата из начального состояния q10 в состояние, в которое по данной букве из своего начального состояния переходит автомат К2.

Для первого специального случая «сцепка» диаграмм переходов конечных автоматов К1 и К2, результатом которой является диаграмма переходов конструируемого недетерминированного конечного автомата К, реализуется в два этапа:

1)идентично тому, как это делается в общем случае, проводятся все дугидубликаты;

2)для каждой буквы х входного алфавита проводится дополнительная дуга (q10, g2(q20,х)) с надписанной над ней буквой х. Как и ранее, начальным

состоянием автомата К объявляется состояние q10, совокупность F «хороших» состояний автомата К считается совпадающей с F2.

Вторым специальным случаем назовем следующую ситуацию: q10 F1 и q20 F2. Специфика ситуации заключается в том, что как в язык L1, так и в язык L2 входит пустое слово; следовательно, пустое слово принадлежит и конкатенации языков L1L2. Отличие алгоритма построения недетерминированного автомата К в данной ситуации от первого специального случая только в назначении множества «хороших» его состояний. В данном случае считается F=F2 {q10}.

Отметим, что процедура синтеза автомата, распознающего конкатенацию языков, определяемых недетерминированными конечными автоматами К*1 и К*2, реализуется идентичным изложенному образом.

Рассмотрим ряд примеров.

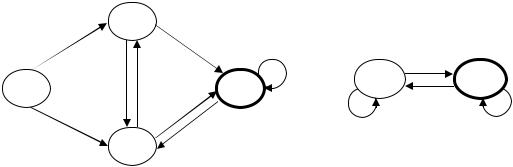
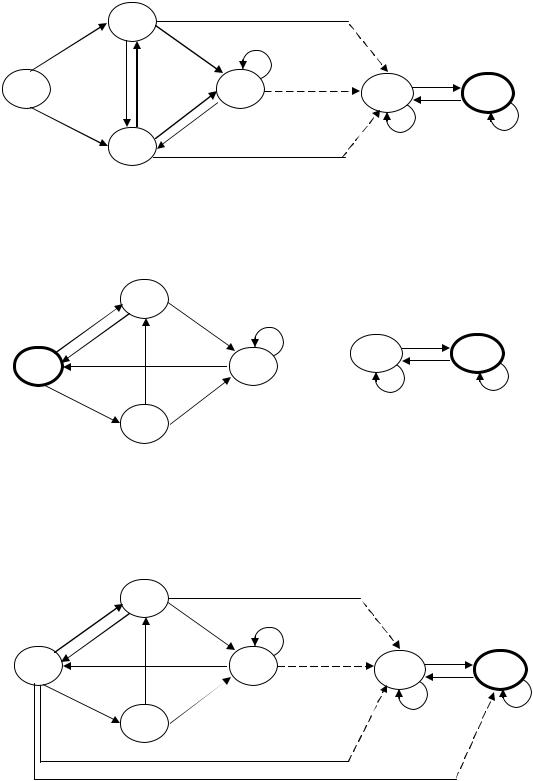
Диаграммами переходов, представленными на рис. 4.1, заданы конечные автоматы, распознающие языки L1 и L2 (отметим, что автомат, распознающий язык L1, недетерминированный). На рис. 4.2 представлена диаграмма переходов недетерминированного конечного автомата, распознающего язык L1L2.

a		q11	a
					b
						b
1	a		b	1	q02	q12
q0				q3		a
			a
b		q21	a		a	b

Рис. 4.1.

		q11			a
a
			a		b
q01	a		b	q31	b	q02	b
							q12
			a				a
			a
b		q21				a	b

a

Рис. 4.2.

q11

a	b	a		b	b
		a		q02	q12
q01			q31
					a
	b
		a		a	b
b	q21

Рис. 4.3.

	q11		b
a	b	a	b
				a		b
		a
q01			q31		q02
	b					q12
		a				a
b	q21				a	b
			a		b
			Рис. 4.4.

q11

a	b	a		b	b
		a		q02	q12
q01			q31
					a
	b
		a		a	b
b	q21

Рис. 4.5.

	q11		b
a	b	a	b
				a		b
		a
q01			q31
	b				q02	q12
		a				a
b	q21				a	b
			a		b
			Рис. 4.6.

После того, как установлена замкнутость класса регулярных языков относительно операции конкатенации, легко доказать замкнутость этого класса и относительно операции возведения в любую целую неотрицательную степень. Пусть L – произвольный регулярный язык. Так как по определению степени языка L1=L, получаем, что L1 – регулярный язык. Предположим, что язык Lk регулярен, здесь k – произвольная натуральная константа. Так как язык Lk+1=LkL является результатом конкатенации регулярных языков Lk и L, то Lk+1

– также регулярный язык. Таким образом, регулярность языка Ln при любом n=1, 2, 3, ... следует из принципа математической индукции. Язык L0 также регулярен, ибо он конечен, имеет в своем составе только пустое слово λ.

Рассмотрение проблемы синтеза по распознающему язык L конечному автомату К конечного автомата К* (вообще говоря, недетерминированного), распознающего язык L*, начнем с частного случая, когда в диаграмме автомата К нет дуг, входящих в вершину q0; состояние q0 в такой ситуации является невозвратным – выйдя из q0 на первом такте работы над любым словом α, автомат К в него никогда уже не вернется. Алгоритм построения по имеющейся диаграмме переходов конечного автомата К диаграммы переходов недетерминированного конечного автомата К*, распознающего язык L*, в данном частном случае (назовем его алгоритмом А) достаточно прост. Через М обозначим совокупность тех дуг (вместе с надписанными над ними буквами) в диаграмме переходов автомата К, которые своими концами имеют вершины из подмножества F данного автомата. Специально отметим, что (в случае их присутствия в диаграмме автомата К) в М входят и петли, т.е. дуги вида (qj, qj),

где qj F. Реализуя алгоритм А, для каждой принадлежащей множеству М дуги (qi, qj) с надписанной над ней буквой х входного алфавита строим дугу-дубликат (qi, q0) с той же надписанной буквой. Начальным состоянием конструируемого автомата считаем q0, это же состояние считаем единственным «хорошим» состоянием в К*. Построение диаграммы переходов автомата К* закончено.

Автомат К* проверяет, принадлежит ли произвольное входное слово α языку L*, т.е. можно ли разбить данное слово на некоторое число р последовательных частей α1, α2,…, αр так, что каждое подслово αi, i = 1, р,

принадлежит L (указанное разбиение оказывается возможным тогда и только тогда, когда существует способ работы данного автомата такой, что обработав тестируемое слово α, автомат оказывается в «хорошем» состоянии).

Действительно, начальную часть произвольного непустого входного слова α конечный автомат К*, начиная работу из состояния q0, обрабатывает в режиме автомата К. Предположение о том, что поступающая на некотором такте произвольная буква х является последней в принадлежащей L первой части входного слова, возникает тогда, когда под воздействием х автомат К может перейти в свое «хорошее» состояние. На данном такте для недетерминированного автомата К* по его построению имеем две возможности:

1)выполнить переход в соответствии с диаграммой автомата К (при этом считается, что данной буквой х часть α1, α1 L, входного слова не заканчивается);

2)под воздействием х по соответствующей дуге-дубликату перейти в состояние q0 (здесь считается, что буквой х завершается часть α1, α1 L, входного слова

α). Если данная буква х оказалась в слове α последней, автомат работу заканчивает, его заключительное состояние оказывается «хорошим», слово α языку L* принадлежит.

Если же данная буква х – не последняя в слове α, то, перейдя по этой букве в состояние q0, автомат К* далее будет вновь функционировать как автомат К; предположение о том, что поступающая в некоторый момент произвольная буква х является последней в принадлежащей L второй части входного слова возникает тогда, когда под воздействием х автомат К может перейти в свое «хорошее» состояние. На данном такте для автомата К* вновь имеются две вышеописанные возможности. Реализация второй возможности означает что данной буквой х заканчивается вторая часть α2, α2 L, входного слова; если данная буква х оказалась в слове α последней, автомат работу заканчивает, его заключительное состояние оказывается «хорошим», слово α языку L*

принадлежит; если же данная буква х – не последняя в слове α, то далее, на каждом очередном этапе, начиная от состояния q0, автомат К* будет вновь функционировать как автомат К, выделяя очередную принадлежащую L часть входного слова.

Представление входного слова α в виде α=α1α2...αр, где каждое подслово αi, i = 1, р, принадлежит L, оказывается возможным тогда и только тогда, когда существует способ работы автомата К* такой, что, обработав тестируемое слово

α, он оказывается в «хорошем» состоянии q0.

Заметим, что, если множество «хороших» состояний автомата К* изменить, считать его совпадающим с множеством F исходного автомата К, то получаемый автомат распознает язык L+.

Применим алгоритм А к диаграмме конечного автомата К, представленной на рис. 4.7. В результате получим диаграмму конечного автомата К* (рис 4.8). Автомат К функционирует в алфавите {a,b,c}и распознает язык L, состоящий из слов, которые начинаются на букву с и в каждом из которых буква с встречается

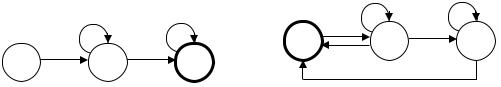
ровно два раза. Автомат К* распознает итерацию языка L. Непустое слово α принимается автоматом К* тогда и только тогда, когда буква с встречается в нем любое четное, отличное от нуля число раз.

			a,b	a,b	a,b
	a,b			c	с
	c	с	q0	q1	q2
				c
q0	q1		q2

	a,b
Рис. 4.7	Рис. 4.8

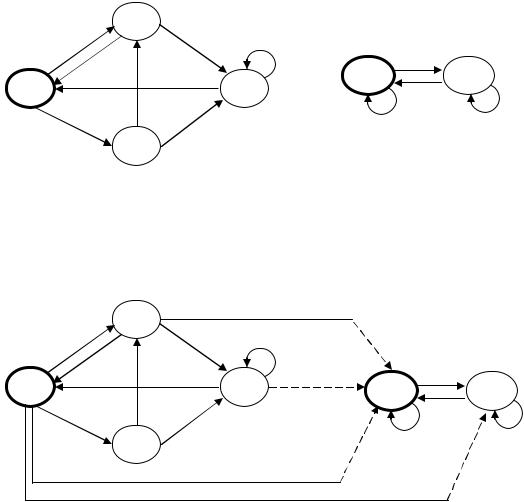
Сейчас рассмотрим определяемый представленной на рис. 4.9 диаграммой конечный автомат К′, распознающий язык L′. Слово α в алфавите {a,b,c}

принадлежит языку L′ тогда и только тогда, когда оно имеет вид аibc, здесь i – произвольное целое неотрицательное число. Если не обратить внимание на тот факт, что начальное состояние автомата К′ не является невозвратным, и непосредственно к диаграмме данного автомата применить алгоритм А, то получим в результате автомат, который распознает язык, являющийся расширением языка (L′)*. В частности, этому языку будут принадлежать не входящие в (L′)* слова а, аа, ааа и т.д. Для того, чтобы построить автомат,

распознающий язык (L′)*, перед применением алгоритма А выполним преобразование автомата К′, обеспечивающее невозвратность начального состояния. Диаграмму переходов автомата К′′ (см. рис. 4.10) по диаграмме автомата К′ строим следующим образом: вводим дублирующее для q0 состояние q01; считаем, что по букве а автомат не остается в состоянии q0, а переходит в состояние q01; из состояния q01 по букве а реализуется петля, по букве b –

переход в состояние q1. Легко видеть, что автоматы К′ и К′′ распознают один и тот же язык L′, но для построения автомата, распознающего (L′)*, к автомату К′′ (его начальное состояние является невозвратным) можно применить алгоритм

А. В результате получаем автомат (К′′)*, диаграмма переходов которого представлена на рис.4.11. (Заметим, что состояние q2 в автомате (K′′)*

становится отрицательно поглощающим, поэтому на диаграмме его можно не изображать.)

a

b с

q0

q1

q2

Рис. 4.9

	a			a
	q0	b		q0		с
			с		b		с
	a	q1		a		q1
			q2				q2
	q01	b		q01		b
	a			a
		Рис. 4.10				Рис. 4.11

Изложим общий алгоритм А0 преобразования произвольного конечного автомата К, в котором состояние q0 не является невозвратным, к

распознающему тот же язык автомату К′ с невозвратным начальным состоянием. С этой целью: для начального состояния q0 автомата К вводим дублирующее состояние q01; все дуги (с надписанными над ними буквами), которые в диаграмме исходного автомата входят в вершину q0, переориентируем в q01 (при этом каждая петля (q0, q0) преобразуется в дугу (q0, q01)); по каждой имеющейся дуге (q0, qi) с надписанной над ней буквой, здесь qi

– произвольное состояние автомата К, проводим дугу (q01, qi) с той же надписанной буквой (при этом для каждой ранее имевшейся петли (q0, q0) проводится, с той же надписанной буквой, петля (q01, q01)); множество

«хороших» состояний автомата К′ считаем совпадающим с множеством

«хороших» состояний исходного автомата К; если q0 F, то q01 также принадлежит F.