лекции / LEKKURS8

Глава 8

РЕКУРСИВНЫЕ ФИЛЬТРЫ.

Во многих применениях играет важную роль один подкласс класса линейных инвариантных к сдвигу систем. Этот подкласс состоит из систем, 0для которых вход x(n) и выход y(n) удовлетворяют линейному разностному уравнению N-го порядка с постоянными коэффициентами.

(1).

Такое численное уравнение ,в частности, мы получим, если входной и выходной сигнал подвергаются системой обработки операции дифференцирования , так что x(t) и y(t) связаны линейным дифференциальным уравнением N-го порядка с постоянными коэффициентами.

Выражая из (1) явно y(n), получим:

(2).

Делая замену обозначений

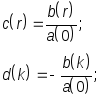(3),

получим выражение цифровогофильтра

(4).

Т.к значение на выходе фильтра y(n) оказывается зависимым от выходных значений в более ранние моменты времени y(n-k), то такой фильтр принять называть рекурсивным. Очевидно , что если все d(k)=0, то то мы придем к нерекурсивному фильтру. Поэтому выражение (4) можно принять за определение цифрового фильтра в общем случае. Обратно, если мы рассматриваем нерекурсивный фильтр, то обязаны предположить, что не все коэффициенты d(k)=0.

Отличительной особенностью рекурсивного фильтра является его большая “ память” по сравнению с нерекурсивным . При этом даже небольшой набор коэффициентов позволяет запомнить все прошлые значения сигнала.

Рассмотрим, например, фильтр ,который описывается разностным уравнением 1-го порядка:

(5),

Пусть входная последовательность x(n) такова, что x(n)=0, если n не равно 0 ,а x(0)=C=const,y(n)=0 при n<0. Иными словами на входе подается дельтаобразный сигнал. Реакцию системы на такой сигнал мы назвали функцией отклика системы или ее импульсной характеристикой . На выходе будем иметь h(n):

(6).

Таким образом, значение x(0) дает о себе знать постоянно в будущем, какое большое n мы бы не взяли. Эта способность помнить значения, которые имели место в отдаленном прошлом является ценным качеством рекурсивного фильтра для многих ситуаций. В связи с этим свойством рекурсивных фильтров они имеют еще одно общепринятое название -фильтры с бесконечной функцией отклика ( БИХ-фильтры). Аналогично, в силу того, что нерекурсивные фильтры способны “помнить” лишь конечное число значений x(n) и передаточная функция такого фильтра равна нулю вне конечных пределов их называют фильтрами с конечной импульсной характеристикой (КИХ-фильтрами).

Хорошо известной операцией , которая представляет собой пример рекурсивного фильтра, является численное интегрирование.

К примеру ,формула интегрирования по правилу трапеций есть рекурсивный фильтр первого порядка:

(7).

Здесь x(n)-значение подинтегральной функции на n-ом узле сетки, а y(n)- значение интеграла (площади).

Численное интегрирование по формуле Симпсона дает пример рекурсивного фильтра второго порядка:

(8)

Ниже мы сравним действие обеих формул как фильтров в частотной области.

Построим передаточную функцию рекурсивного фильтра.

Для этого можно либо в качестве входного сигнала взять собственную функцию линейного инвариантного с сдвигу фильтра- комплексную экспоненту, либо воспользьоваться свойством сдвига преобразования Фурье. Последуем второму методу.

Согласно свойству сдвига преобразования Фурье, если

то (9).

Переходя в (1) к образам Фурье c использованием свойства сдвига (7) получим:

(10).

Находя из (8) отношение Фурье-образов входного и выходного сигналов , получим искомую передаточную функцию:

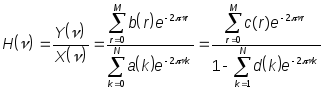(11).

Вводя обозначение

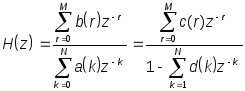(12).

В формулах (9) и (10) a(k) и b(k) есть коэффициенты в правой и левой частях разностного уравнения (1).

Таким образом, если рассмотрим комплексную z-плоскость, то значения передаточной функции можно получить из (12) взяв точки плоскости, лежащие на единичной окружности, на которой частота изменяется от -1/2 до 1/2, где за единицу взята частота Найквиста.

Числитель и знаменатель передаточной функции представляют собой полиномы от 1/z степени M в числителе и степени N в знаменателе. То , что передаточная функция системы равна отношению полиномов от 1/z является характерной чертой систем, описываемых линейными разностными уравнениями с постоянными коэффициентами.

Найдем передаточные функции формул интегрирования по правилу трапеций и по формуле Симпсона.

Согласно формулам (9) и (10) передаточная функция первого фильтра равна

(13).

Чтобы оценить качество такого фильтра удобно сравнить полученную передаточную функцию, с идеальной передаточной функцией , которую рассчитывают из точного значения интеграла.

Точное значение интеграла от комплексной экспоненты

равно 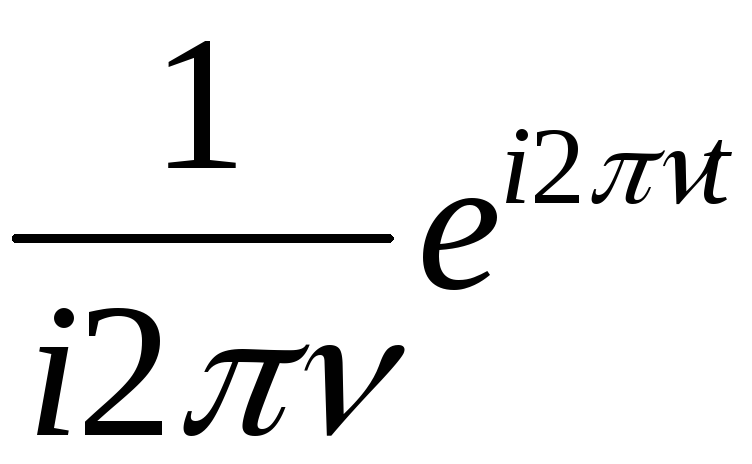. Поэтому в качестве идеальной передаточной функции интегрирующего фильтра возьмем .

Отношение точного значения интеграла к приближенному равно:

(14).

Аналогичный анализ интегрирования по формуле Симпсона

дает следующее отношение численной к точной передаточной функции

(15).

Следующий график дает сравнительный анализ чис

ленного интегрирования по формуле трапеций и по формуле Симпсона.

Рис.4 Частотные характеристики формул численного

интегрирования.

Из рисунка ясно, что при наличии шума (т.е. случайных высокочастотных компонентов), формула Симпсона более опасна, чем формула трапеций. Но когда в интегрируемой функции малы высокочастотные компоненты, то плоский характер передаточной функции делает формулу Симпсона более предпочтительной.

Поскольку полином степени N имеет ровно N -корней, то передаточная функция как функция переменной z имеет M нулей и N полюсов. Следовательно, с точностью до постоянного множителя передаточная функция может быть полностью описана картиной полюсов и нулей в z -плоскости.

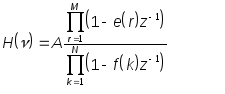(16).

Эта форма представления передаточной функции называется последовательной. Очевидно, что максимумы передаточной функции будут наблюдаться вблизи ее полюсов, т.е. там, где знаменатель имеет маленькое значение. Чтобы геометрически проиллюстрировать принцип действия рекурсивного фильтра удобно перейти к третьей форме передаточной функции , называемой параллельной.

Эту форму передаточной функции можно построить, если воспользоваться алгебраическим правилом разложения отношения многочленов на простейшие дроби

(17)

Т.к. корни знаменателя могут быть и действительные и комплексные, то коэффициенты f (k) и g(k) ,вообще говоря, комплексные. Чтобы представить передаточную функцию в виде суммы простейших дробей с положительными коэффициентами, выделим отдельно сумму с действительными и отдельно с мнимыми f(k). Учитывая при этом , что комплексные корни уравнения с действительными коэффициентами могут появляться только сопряженными парами, получим разложение передаточной функции на сумму простейших дробей:

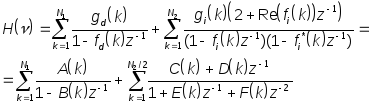(18)

Таким образом любой рекурсивный фильтр можно представить в виде суммы фильтров первого и второго порядков. Такую форму рекурсивного фильтра называют параллельной.

Представляя передаточную функцию набором полюсов и нулей , несложно геометрически наити значение передаточной функции. Воспользуемся параллельной формой (17) рекурсивного фильтра и построем геометрически передаточную функцию для одного его звена . Т.е. найдем значения передаточную функции этого звена фильтра на единичной окружности в z-плоскости.Обозначая f(k)=р будем иметь искомую передаточную функцию:

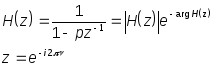(19).

Найдем коэффициент усиления этого звена фильтра.

(20).

Поскольку z=0 нуль передаточной функции, z=p -полюс передаточной функции, то коэффициент усиления фильтра на частоте равен отношению длины вектора, выходящего из нуля в соответствующую точку единичной окружности

( соответствующую частоте) , к длине вектора , идущего из полюса в эту же точку единичной окружности. Поэтому, когда точка на единичной окружности z-плоскости окажется на минимально возможном расстоянии от полюса, будет наблюдаться максимальное усиление входного сигнала. Если нужно усилить частоту в сигнале, то нужно в полюс поместить в точку с аргументом . Абсолютную величину усиления фильтра на этой частоте можно определить, задавая соответствующее расстояние от нуля полюса. Чем ближе полюс расположен к единичной окружности, т.е. чем дальше он от нуля, тем больший будет коэффициент усиления на резонансной частоте.

Таким образом, размещая нужным образом полюса передаточной функции, можно получить фильтр, усиливающий заданным образом сигнал на определенных частотах.

Очевидно, что на коэффициенты рекурсивного фильтра нужно накладывать некоторые ограничения, чтобы избежать слишком малых значений знаменателя, при которых передаточная функция бесконечно возрастает.

Эти требования формулируются как условие устойчивости системы.

Устойчивой системой назовем систему, в которой каждый ограниченный входной сигнал создает ограниченный выходной сигнал. Линейная инвариантная к сдвигу система устойчива тогда и только тогда, когда

(21).

Для примера выясним, при каких значениях параметра а устойчив рассмотренный выше фильтр (5).

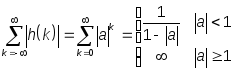
Следовательно, рассматриваемая система устойчива только при .

В общем случае поскольку элементарное звено любого фильтра имеет вид (5), то условие устойчивости фильтра приводит к требованию, чтобы все полюса и нули передаточной функции по абсолютной величине были меньше единице , т.е. лежали внутри единичной окружности в z-плоскости.

Одним из свойств, которые приводят к трудностям при применении рекурсивных цифровых фильтров является их нелинейная фазовая зависимость. Например, фазовый сдвиг одного звена фильтра согласно его определению (14) равен аргументу вектора, выходящего из нуля минус аргумент вектора , выходящего из полюса. Очевидно, что фазовый сдвиг такого фильтра равен нулю при частоте =-1 и дальше линейно растет до некоторого значения вблизи =0 слева , где он резко изменяется от некоторого положительного значения до такого же отрицательного значения справа от =0 и далее снова линейно возрастает до 0 на правом конце интервала Найквиста.

Фазовый сдвиг фильтра показан на рисунке.

Такая нелинейная фазовая характеристика рекурсивного фильтра может привести к серьезной деформации сигнала, поскольку появление фазового множителя в частотной области ведет к изменению сигнала во временной области.В отличие от рекурсивного фильтра фазовый сдвиг нерекурсивного фильтра является линейной функцией частоты и поэтому , согласно свойству сдвига, ведет только к некоторому смещению выходного сигнала во времени как целого.

Рассмотрим некоторые методы проектирования БИХ-фильтров.

Вспомним, что КИХ-фильтры рассчитывались разложением передаточной функции в ряд Фурье, коэфициенты которого и рассматривались как коэффициенты фильтра. Но известно , что коэффициенты Фурье совпадают с коэффициентами, рассчитанными методом наименьших квадратов.

Воспользуемся этой же идеей и для рекурсивных фильтров .

Для этого необходимо определить требуемую частотную характеристику для дискретного ряда частот. Составить среднеквадратичное отклонение требуемой передаточной функции от модельной, заданной параметрами в прямом(10), последовательном (11) или параллельном (12) виде.

Нужно найти значения параметров фильтра, минимизирующих среднеквадратичную ощибку. Для этого нужно взять производные по каждому из параметров и приравнять их к нулю. Поскольку рекурсивный фильтр порядка N имеет не более 2N+1 параметров, то взяв по кажной из них производную и приравняв ее к нулю получим систему из 2N+1 уравнений с 2N+1 неизвестными. Эту систему можно решить численно, применяя методы оптимизации .

Сделаем несколько замечаний оотносительно такой процедуры расчета параметров фильтра. Во первых, при такой процедуре , поскольку среднеквадратичное отклонение рассчитывается по абсолютной величине, учитывается только амплитудная характеристика заданного фильтра. Во- вторых, алгоритм оптимизации может в итоге дать параметры, соответствующие неустойчивому фильтру, т.е. полюсы и нули могут оказаться за пределами единичного круга.

При проектировании типовых фильтров часто используются фильтры , для которых задана конкретная зависимость квадрата модуля передаточной функции от частоты.

1.Фильтр Баттерворда.

2.Фильтр Чебышева.

где полином Чебышева N-го порядка.

3.Эллиптический фильтр.

где - эллиптическая функция Якоби.

При проектировании низкочастотных фильтров обычно задают следующие параметры: максимальная величина ослабления в полосе пропускания, максимальная величина усиления в полосе запирания, правую и левую границы переходной полосы.

Рассмотрим , например,как спроектировать по таким данным низкочастотный фильтр Баттерворда.

Пусть требуется рассчитать фильтр со следующими характеристиками: при частоте ,

при частоте < , где левая и правая границы переходной полосы , соответственно. Из условий на границах переходной полосы можем получить частоту среза и необходимый порядок фильтра:

(16)

Исключая из уравнений частоту среза, можем найти порядок N и ,с его помощью, частоту среза фильтра.

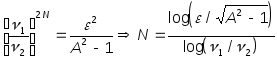(17)

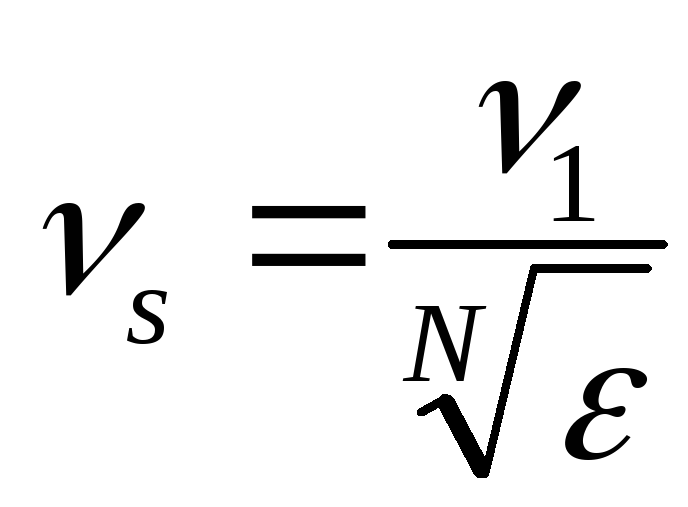(18)

Для полного расчета фильтра теперь нужно найти полюса фильтра.

(19)

Рассмотрев основные принципы, лежащие в построении нерекурсивных и рекурсивных фильтров, подведем некоторые итоги. Главным преимуществом рекурсивных фильтров является их способность иметь очень узкую переходную полосу при относительно небольшом наборе коэффициентов. Поэтому их сремятся использовать при обработке больших массивов данных. Однако, когда машинное время не составляет серьезной проблемы, то нерекурсивные цифровые фильтры оказываются более предпочтительными т.к. они проще по пониманию, расчету и применению. Например , для них нет проблемы неустойчивости.

Еще одним важным преимуществом нерекурсивных фильтров является их линейный фазовый сдвиг, что приводит лишь к некоторому смещению во временной области сигнала как целого.

Нелинейный сдвиг фазы, осуществляемый рекурсивным фильтром приводит к деформации сигнала во временной области и поэтому требует дополнительной операции устранения такого сдвига ( двойной фильтрацией).

Преимуществом рекурсивных фильтров является то , что они используются в реальном времени и поэтому имеют значительно меньшую задержку на выходе. Это связано с тем , что рекурсивные фильтры являются физически реализуемыми. Принцип причинности требует , чтобы отклик на сигнал поступал не ранее, чем поступит сам сигнал: причина должна предшествовать следствию. Т.е. при расчете y(n) через значения x(m) и y(m) значения индексов m не должны превышать значения индекса n.

Согласно определению рекурсивных фильтров (1) и (2) , они удовлетворяют принципу причинности.

Наоборот, типовой нерекурсивный фильтр является физически нереализуемым, т.к. он требует знания данных из будущего. Поэтому нерекурсивный фильтр можно реализовать, если осуществить необходимую задержку данных на выходе. Например, при сглаживании данных пятерками т.к. для вычисления y(n) требуются значения x(n+1) и x(n+2) из будущего, нужно осуществить задержку на выходе на два временных отсчета. Таким образом термин физическая реализуемость для цифровой обработки будем понимать в смысле реализуемости в реальном времени.

Как известно, одной из характеристик фильтра является коэффициент усиления фильтра. Однако для некоторых типов фильтров коэффициент усиления в зависимости частоты может меняться на несколько порядков и в обычном масштабе такая зависимость перестает быть достаточно информативной. По этой причине в таких случаях лучше пользоваться логарифмической шкалой. Для этой цели обычно применяют децибелы, обозначаемые Дб и определяемые как

Дб (32).

Например, если коэффициент усиления фильтра на некоторой частоте равен 1000, то этот результат можно сформулировать иначе как усиление в 60 Дб. При этом характерной точкой является точка, в которой мощность сигнала возрастает или падает в 2 раза . В логарифмическом масштабе такое усиление равно 3 Дб (ослабление -3Дб), поэтому эту точку тазывают 3-х децибелловой.

На графике зависимости переходной функции от частоты эта точка как раз и соответствует частоте среза.

В децибеллах обычно задают допустимую величину величину пульсаций в полосе пропускания и в полосе запирания при проектировании фильтров.

Рассмотрим еще одну важную проблему, касающуюся проектирования и использования цифровых фильтров, касающуюся эффектов конечной арифметики. Мы рассматривали действия, которые выполняются цифровыми фильтрами так, как будто арифметические вычисления выполняются точно, без жесткого округления. Однако, на практике использование чисел с конечной длиной слова вызывает нежелательные последствия.