Глава 7. Дискретное преобразование фурье. Дискретная свертка.

Мы рассмотрели две формы преобразования Фурье :

1) Преобразование Фурье в непрерывном времени с непрерывным изменением частоты

2) преобразование Фурье в дискретном времени с непрерывным изменением частоты.

Но в реальной ситуации временные последовательности всегда имеют конечную длительность. Кроме того, значительно большие возможности для обработки данных появляются, если использовать не аналоговые, а дискретные преобразователи Фурье, которые и частотные характеристики представляют в виде конечных числовых последовательностей. При этом возрастает как качество обработки информации, так и скорость ее обработки за счет того, что существуют эффективные способы вычисления таких преобразований в дискретном виде и , как следствие, возможность обработки массивов большего размера. Способ представления сигналов в виде конечных цифровых последовательностей, в результате обработки которых также получается некоторая конечная цифровая последовательность и составляет сущность цифровой обработки сигналов. Основой цифровой обработки сигналов является особая форма преобразования Фурье, называемая дискретным преобразованием Фурье (ДПФ).Как увидим ниже ДПФ есть преобразование Фурье временной последовательности конечной длины, являющееся само по себе конечной последовательностью, а не непрерывной функцией , и соответствует равноудаленным по частотам выборкам преобразования Фурье сигнала. Кроме своей теоретической важности,ДПФ играет центральную роль при обработке сигналов вследствие существования эффективного алгоритма его вычисления, так называемого быстрого преобразования Фурье (БПФ) .

7.1 Дискретизация частотной оси.Дискретное преобразование Фурье

Введем ДПФ, основываясь на преобразовании Фурье в дискретном времени (2). Поскольку теперь мы имеем дело с конечной последовательностью (длиной N), то положим, что временная последовательность x(n)=0 при n<0 и при n>N-1. Как будет видно из дальнейшего, дискретизация частотного интервала, т.е. вычисление Фурье-образа только в кратных значениях частот приведет также к периодическому продолжению исходной временной последовательности по оси времени. Чтобы опять избежать наложения, пользуясь аналогией с временной дискретизацией, дискретизуем ось частот с интервалом

, где NT -полный временной интервал задания исходной функции. Тогда значение частоты на k-ом частотном отсчете , а k изменяется от 0 до N-1(т.к. , согласно теореме дискретизации). Таким образом, число отсчетов по частоте равно также N.

Если это сделано, то преобразование Фурье (2) примет вид:

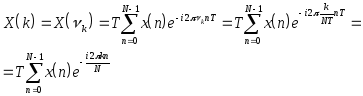(3)

7.2 Ортогональность системы комплексных экспонент на множестве равноотстоящих точек.

Чтобы перейти от прямого преобразования Фурье к обратному,

докажем ортогональность комплексных экспонент

(или что тоже самое, систем синусов и косинусов) на множестве равноотстоящих N точек.

(4)

Обозначая разность n-n’ за m ,получим в правой части (4) геометрическую прогрессию со знаменателем , при этом отметим очевидное равенство . Находя по известной формуле сумму этой геометрической прогрессии, получим

(5)

При этом мы использовали тот факт, что

в случае m=0,±N, ±2N,....

Как будет показано ниже, эти значения и приводят к эффекту наложения или подмены частот, появляющемуся при равномерной дискретизации функции.

Отметим, что приведенная система экспонент ортогональна на системе любых отсчитанных подряд N точек, независимо от выбора начальной. Действительно, взяв за начальную точку с индексом -l делая замену переменной суммирования k’=k+l, получим:

(5a)

т.к. , а при остальных k значение суммы равно нулю.