ОАиП / 6 лаба / Теоретические сведения к рекуррентным вычислениям

Рекуррентные вычисления

Рассмотрим числовую последовательность a_1, a_{2, …,} a_n .

Рекуррентная формула — формула вида 

,

выражающая каждый член последовательности   через  p предыдущих членов.

Общая проблематика вычислений с использованием рекуррентных формул является предметом теории рекурсивных функций.

Частными случаями линейных рекуррентных последовательностей являются последовательности:

• арифметическая прогрессия

• геометрическая прогрессия

• числа Фибоначчи

• числа Люка

• числа трибоначчи

• последовательности Люка

• Арифмети́ческая прогре́ссия — числовая последовательность 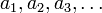 , в которой каждый член, начиная со второго, есть сумма предыдущего члена и некоторого постоянного числа 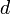, называемого разностью или шагом арифметической прогрессии.

• Зная первый член арифметической прогрессии 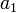 и ее разность 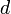, можно последовательно находить остальные члены с помощью реккурентного соотношения 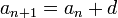, которое вытекает из определения.

Геометри́ческая прогре́ссия — последовательность чисел  (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число  (знаменатель прогрессии), где , : ^[1].

Чи́сла Фибона́ччи — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS)

в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного какФибоначчи)^[1]. Иногда число 0 не рассматривается как член последовательности.

Более формально, последовательность чисел Фибоначчи  задается линейным рекуррентным соотношением:

Числа Люка задаются рекуррентной формулой

с начальными значениями  и .

Последовательность чисел Люка начинается так:

2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, …

Чи́сла трибона́ччи — последовательность целых чисел , заданная с помощью линейного рекуррентного соотношения:

.

Название является вариацией «чисел Фибоначчи» — с добавкой «три» (лат. tri-), обозначающей количество суммируемых чисел.

Последовательность чисел трибоначчи начинается так:

0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, 121415, 223317, 410744, 755476, 1389537, 2555757, 4700770, 8646064, 15902591, 29249425, 53798080, 98950096, 181997601, 334745777, …

Пример использования цикла For()

Постановка задачи:

Найти N-й член ряда, если дано значение первого и второго членов ряда, а каждый последующий вычисляется по формуле

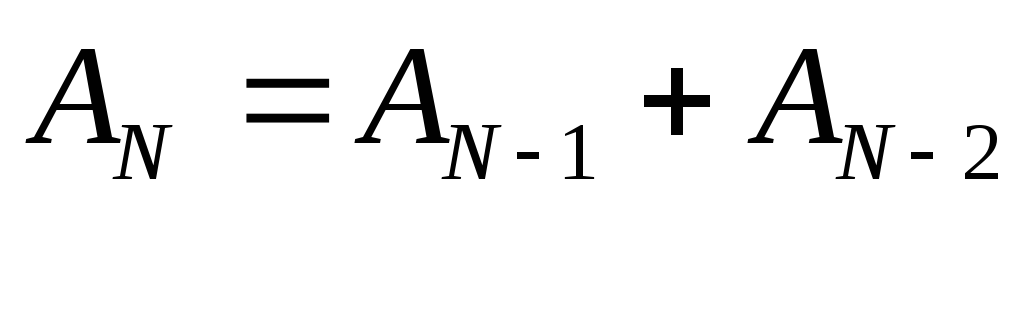
Исходные данные:

- значение первого члена ряда

- значение второго члена ряда

- номер искомого члена ряда

Результаты:

- значение члена ряда под заданным номером.

Таблица соответствия переменных:

Имя переменной В условии	Имя переменной В программе	Тип переменной	комментарий
A1	а1	Float	Первый член ряда
A2	а2	Float	Второй член ряда
An	аn	float	N-й член ряда
N	n	Int	Номер искомого члена ряда
	i	Int	Счетчик цикла

БЛОК-СХЕМА ЗАДАЧИ

i=2

an=a1+a2

a1=a2

a2=an

i=i+1

Текст программы.

/*подключение стандартных библиотек*/

#include<stdio.h>

#include<conio.h>

main()

{

/*описание используемых переменных с их типами*/

float a1,a2,an;

int n,i;

clrscr;

/*ввод исходных данных*/

puts("введите значение первого элемента последовательности");

scanf("%f",&a1);

puts("введите значение второго элемента последовательности");

scanf("%f",&a2);

puts("введите номер рассчитываемого элемента последовательности");

scanf("%i",&n);

/*Расчет N-го элемента последовательности.

Изначально счетчик цикла равен 3 , так как два первых элемента

последовательности нам даны и расчет надо начинать с 3 элемента*/

for(i=3;i<=n;i++)

{

an=a1+a2; /*в переменную an занести сумму двух предыдущих членов*/

a1=a2; /*переменной а1 присвоить значение предыдущего члена послед-ти */

a2=an; /*переменной an присвоить значение полученного члена послед-ти*/

}

/*вывод результатов*/

printf("значение %i элемента последовательности=%2.2f",n,an);

}

ТЕСТЫ:

Тест1:

а1=2

а2=7

n=9

an=173

Тест2:

a1=2

a2=-5

n=15

an=-1419

Задача 4. Вычисление суммы ряда с заданной точностью.

Составить графическую схему алгоритма и программу вычисления суммы ряда с точностью для заданных значений х и .

Вывод формулы рекуррентного соотношения для n-ного члена ряда

;

;

;

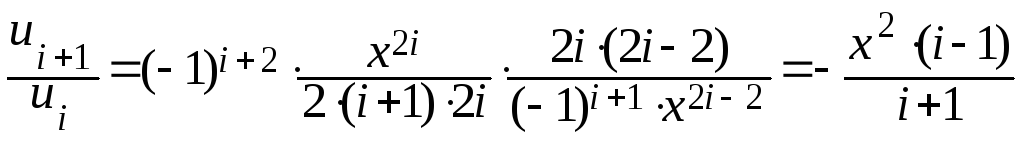, где , i=1,2, …

Таблица соответствия переменных

Имя переменной в условии	Имя переменной в программе	Тип	Комментарий
x	x	float	Аргумент
ε	Eps	float	Точность
S	S	float	Сумма ряда
—	i	int	Параметр цикла
—	u	float	Произвольный член ряда

Тест

X=0,09

Eps=0,000001

S=0.9989023

Графическая схема алгоритма

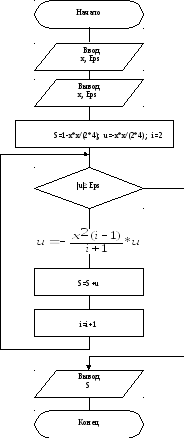
Нет

Да

Задача 5. Табулирование функции, заданной в виде ряда.

Вычислить и вывести на экран в виде таблицы значения функции, заданной с помощью ряда Тейлора, на интервале от x_нач до x_кон с шагом dx с точностью . Таблицу снабдить заголовком и шапкой. Каждая строка таблицы должна содержать значение аргумента, значение функции и количество просуммированных членов ряда.

Графическая схема алгоритма

Нет

Да

Нет

Да

Таблица соответствия переменных

Имя переменной в условии	Имя переменной в программе	Тип	Комментарий
xнач	x_n	float	Левая граница интервала
xкон	x_k	float	Правая граница интервала
dx	dx	float	Шаг табулирования
ε	eps	float	Точность вычисления
x	x	float	Аргумент функции
—	y	float	Значение функции
—	i	int	Номер члена ряда
—	u	float	Значение i-ого члена

Вывод формулы рекуррентного соотношения для i-ого члена ряда

;

;

;

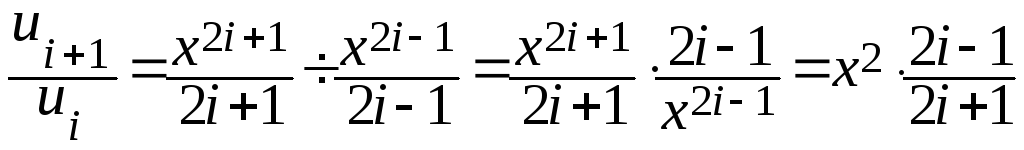, где , i=1,2, … .

Тест

x_нач=-0,4; x_кон=0,6; dx=0,2; ε=0,000001.

В таблице должна быть 51 строка.

При x=0,2 y= 0,20273255; Arth(0,2)=0,20273255