3-7_-_Mekhanika

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Описания лабораторных работ Учебной лаборатории физического эксперимента

физического факультета СПбГУ

Часть 1

МЕХАНИКА

Санкт-Петербург 2013

Печатается по постановлению Ученого совета физического факультета СПбГУ от 15 октября.2013г.

Ответственный редактор: В.И. Коротков.

Составители: Е.П. Зароченцева, И.С. Бобкова, С.О. Высоцкая, Б.Д. Катунин, Д.А. Лисаченко, Т.В. Рудакова, М.Н. Букина, С.А. Кудря, Н.А. Малешина.

Рецензенты: профессор И.Ч. Машек, ст. преподаватель В.И. Ролич

Описания лабораторных работ Учебной лаборатории физического эксперимента физического факультета СПбГУ.

Часть 1: Механика / Е.П. Зароченцева, И.С. Бобкова и др.; Под ред. В.И. Короткова;

СПб., 2013. –41 с.

Данное пособие содержит описания лабораторных работ по разделу «Механика» курса общей физики и представляет собой существенно переработанное и дополненное переиздание учебного пособия «Механика Ч. 1. / Под ред. В.Е. Холмогорова» (Л.: Изд-во ЛГУ, 1989. –41 с.). Каждая лабораторная работа рассчитана на 4 академических часа. Студент допускается к выполнению лабораторной работы после самостоятельного изучения необходимой теории, ознакомления с порядком выполнения основных операций и сдачи зачёта по технике безопасности. Предназначено для студентов факультетов: биологопочвенного, географии и геоэкологии, геологического, медицинского, химического и др.

©Е.П. Зароченцева, И.С. Бобкова и др.,

©Санкт-Петербургский государственный

университет, 2013.

2

СОДЕРЖАНИЕ
Тема: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕ-
НИЯ ТВЕРДОГО ТЕЛА. Введение……………………...	4
Лабораторная работа № 3
ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ
ВРАЩАЮЩИХСЯ ТЕЛ………………………….............	8
Тема: УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ.
Введение……………………………………………………	15
Лабораторная работа №4
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО
ПАДЕНИЯ С ПОМОЩЬЮ ОБОРОТНОГО МАЯТ-	16
НИКА………………………………………………
Тема: ДЕФОРМАЦИЯ ТВЕРДОГО ТЕЛА.	23
Введение……………………………………………………
Лабораторная работа № 5
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ПО РАСТЯЖЕ-	27
НИЮ ПРОВОЛОКИ……………...………………………
Лабораторная работа № 6
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА СТЕРЖНЯ	30
КРУГЛОГО СЕЧЕНИЯ ПО КРУЧЕНИЮ……………
Лабораторная работа №7
ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА ОДНОРОД-
НОГО СТЕРЖНЯ КРУГЛОГО СЕЧЕНИЯ МЕТО-
ДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ…………………	34
Литература……………………………………...................	38
Приложение……………………………………………….	39

3

Тема: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Введение

При вращательном движении точечное тело движется по

окружности. Его положение задается радиус - вектором, R направленным из центра окружности в точку, где находится тело.

На рис. 1 тело в течение интервала времени t: переместилось из точки 1 в точку 2. При этом радиус - вектор повернулся на угол φ. Угол поворота является основной кинематической характеристикой при описании вращательного движения. Угол поворота принято опреде-

Рис. 1

лять как вектор

φ, на-

правление которого связано с направлением вращения тела правилом правого винта. Для

определения направления φ следует, мысленно вращать рукоят-

ку винта в направлении движения тела по окружности. Тогда направление движения жала винта укажет направление вектора угла поворота (рис. 1). В системе СИ величина угла поворота измеряется в радианах.

Вращательное движение характеризует угловой скоро-

стью:

ω =	d φ	,	(1)
	dt

а изменение угловой скорости характеризуется угловым ускорением:

	β =	d ω	,	или	β =	d	d φ	=	d 2φ	(2)
		dt				dt			dt2
							dt

Векторы всех угловых физических величин ( φ, ω и β )

4

Рис. 2

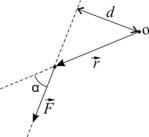
направлены вдоль оси вращения перпендикулярно плоскости, в которой происходит движение. Если движение по окружности ус-

коренное, то векторы ωи β направлены одинаково, а если движение замедленное, то их направления взаимно противоположны.

На рис. 1 точечное тело перемещается по окружности за время t из точки 1 в точку 2. Пройденный путь S при этом соответствует длине дуги, соединяющей эти точки. При t → 0 угол, на который поворачивается радиус - вектор, мал. Следовательно, можно считать, что

	sin φ ≈ φ =	S	, откуда	S = φ R	(3)
		R

Дифференцируя по времени последнее выражение, получим линейную скорость точки V, которая направлена по касательной к траектории:

dS	=	d φ	R.	(4)
dt		dt
Следовательно:
V = ω R.				(5)

Дифференцируя по времени еще раз, получим:

	dV	=	d ω	R	a =β R,	(6)
	dt		dt
					t

где at - модуль тангенциального ускорения.

В векторном виде:
V = ω R		и	a	= β R	,	(7)
			t

Квадратные скобки в последних формулах означают векторное произведение.

Всякое движение тел начинается вследствие их взаимодействия с другими телами. Мерой взаимодействия служит сила.

Так, если на покоящееся тело начинает действовать сила, то тело приходит в движение в направлении действия силы с ус-

5

корением, пропорциональным величине этой силы (второй закон

Ньютона): F = ma , где коэффициент пропорциональности m называется массой тела и служит мерой его инерции.

Однако, для начала вращательного движения вокруг некоторой оси О, мало того, чтобы на тело подействовала сила. Необходимо, чтобы была связь, удерживающая тело на постоянном расстоянии от оси.

Для описания вращательного движения вводится величина, называемая моментом силы. Рассмотрим точечное тело способное вращаться вокруг оси, расположенной перпендикулярно плоскости рисунка и пронизывающей эту плоскость в точке O

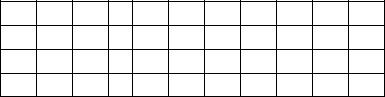
(рис. 2). Положение тела относительно точки О задается радиус -

вектором r . Пусть к телу приложена сила F так, что линия действия силы составляет угол α с направлением вектора r . Моментом

силы M называется векторное произведение векторов r и F :

		(8)
M = r F .
Модуль момента силы определяется выражением:
M = r F sinα.		(9)

Направление вектора M определяется правилом правого винта: если поворачивать головку винта так, чтобы вектор r по крат-

чайшему пути поворачивался к вектору F (начала векторов совмещены) то, направление движения винта укажет направление вектора

M . Таким образом, момент силы направлен всегда по оси враще-

ния перпендикулярно плоскости, в которой происходит движение. На

рис. 2 вектор M направлен на нас. Кратчайшее расстояние от оси вращения до линии действия силы (d на рис. 2) называется плечом силы.

d = r sinα.

(10)

Тогда выражение для модуля момента силы можно перепи-

6

сать в виде:

M = F d.

(11)

Если на покоящееся тело начинает действовать момент силы, то тело приходит во вращательное движение с угловым ускорением, направленным туда же, куда направлен вектор момента силы. Величина углового ускорения пропорциональна величине действующего момента силы (основное уравнение динамики вращательного движения):

M = I β,

(12)

где коэффициент пропорциональности I называется моментом инерции тела и служит мерой его инерции при вращательном движении. Для точечного тела момент инерции определяется произведением его массы на квадрат радиуса окружности, по которой тело движется:

I = mr2.

(13)

Твердое тело (неточечное) можно рассматривать как систему жестко связанных материальных точек.

Пусть твердое тело массой m разбито на N точечных тел.

N

Тогда m = ∑mi , i=1

где mi , масса i -го точечного тела.

Так как при вращательном движении все части тела движутся с одинаковым угловым ускорением, то уравнение движения i -го тела может быть написано в виде:

				Mi = Ii β,	(14)
где	I	i	= m r 2	- момент инерции i -го точечного тела,	r - кратчай-
			i i		i

шее расстояние от i -го тела до оси вращения.

Тогда легко получить уравнение движения для всего твердого

тела:

N	N
∑Mi =β∑Ii M = I β,		(15)
i=1	i=1

где M - результирующий момент, действующий на тело, а

N	N
I = ∑Ii = ∑ mi ri –		(16)
i=1	i=1
		7

– момент инерции твердого тела.

Лабораторная работа № 3

ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАЮЩИХСЯ ТЕЛ

Прежде чем приступить к работе, необходимо ознакомиться с введением по теме: «Динамика вращательного движения твердого тела»

ЦЕЛЬ РАБОТЫ: Экспериментальная проверка основного закона динамики вращающегося тела (15). Необходимо экспериментально подтвердить, что:

•при неизменном моменте инерции тела I угловое ус-

корение пропорционально моменту действующей силы, т.е. при

I = const β M ;

• при постоянном моменте силы M, действующей на тело, угловое ускорение обратно пропорционально моменту инерции

тела, т.е. при M = const β 1I .

Определить моменты инерции маятника для исследованных положений грузов на спицах крестообразного маятника.

Описание экспериментальной установки.

Установка, на которой выполняется лабораторная работа, состоит из механических частей и электронного блока (см. фото). Механическая часть представляет собой крестообразный маятник Обербека (1), который может вращаться вокруг горизонтальной оси. Соосно с маятником закреплен блок (2), состоящий из двух шкивов, на которые наматывается нить, и стопорного устройства (7). Момент инерции маятника может изменяться при перемещении регулировочных грузов (3). Нить (4) перекидывается через неподвижный блок (5) и к её концу подвешивается груз (6) с регулируемой массой.

8

Электронная часть представлена блоком, подключенным к стопорному устройству (7) и фотодатчику (8). Электронный блок осуществляет разблокировку стопорного устройства и подсчет вре-

Внешний вид установки

мени движения груза (6) от момента разблокировки до срабатывания фотодатчика (8). Измеренное время в секундах и их долях отображается на цифровом табло.

Подготовка к выполнению работы и правила работы с электронным блоком.

9

Перед началом измерений при выключенном электронном блоке убедитесь, что:

•маятник свободно вращается вокруг своей оси;

•нить намотана на один из шкивов блока 2 и при вращении маятника ничего не задевает;

•груз 6 при движении вниз пересекает фотодатчик 8;

•регулировочные грузы на спицах 3 находятся на равных расстояниях от оси вращения маятника.

1.Включить электронный блок с помощью зеленой кнопки на задней панели прибора; при этом автоматически сработает стопорное устройство, и вращение маятника будет заблокировано. Вращать

маятник при застопоренном блоке категорически запрещается!!!

2.Привести установку в исходное состояние, для чего снять блокировку, нажав кнопку «Стоп», и, вращая маятник по часовой стрелке, поднять груз до уровня красного указателя, следя за правильностью намотки нити.

3.Нажать кнопку «Стоп» на электронном блоке, удерживая маятник в этом исходном положении. (При этом сработает стопорное устройство, а счетчик времени обнулится.)

4.Нажать кнопку «Старт» на электронном блоке. При этом блок

2расстопорится и груз 6 начнет опускаться вниз. Одновременно с этим начнется отсчет времени на цифровом табло измерительного прибора. При достижении грузом 6 фотодатчика 8 отсчет времени остановится, и блок 2 застопорится.

5.Записать показания времени с табло электронного блока. Примечание: включайте электронный блок только на время

выполнения измерений. По завершении измерений выключите электронный блок.

Физическое обоснование эксперимента.

Вращающаяся часть маятника состоит из четырех спиц, закрепленных во втулке под прямым углом друг к другу. На ось втулки насаженны два легких шкива различных радиусов (R1 и R2). Вращение происходит вокруг горизонтальной оси.

Момент инерции системы относительно оси вращения можно изменять, перемещая грузы вдоль спиц. Каждый раз, закрепляя грузы на спицах на определенном расстоянии от оси вращения, необходимо проверять, правильно ли сбалансирована система, т.е. находится ли она в положении безразличного равновесия. Для проверки необходимо маятник вывести из равновесия и убедиться, что он с одинаковой вероятностью останавливается в любом положении.

10

Момент силы, вызывающий вращение маятника, создается натяжением нити, навитой на один из шкивов, под действием груза Р.

Момент силы можно изменить, подвешивая к нити грузы различной массы или изменяя плечо силы, для чего нить закрепляется на шкивах разного радиуса.

Под действием груза P нить разматывается и приводит во вращение крестовину маятника. Измеряя время t, в течение которого груз P из состояния покоя опустился на расстояние H, можно определить линейное ускорение груза:

	a =	2H	,	(3.1)
		t2

Линейное ускорение груза будет равно тангенциальному ускорению точек на ободе шкива. Тогда, зная радиус шкива R, можно найти угловое ускорение маятника:

β =	a	.	(3.2)
	R
Если Fн - сила натяжения нити, а P = mg			- вес груза, то
справедливо соотношение: ma = P −Fн.
Следовательно, величина вращающего момента Mн равна:
Mн = FнR = (P −ma)R = m(g −a)R,			(3.3)

Это выражение справедливо, если можно пренебречь силами трения, то есть, если можно считать, что момент сил трения

M тр << Mн . В действительности это не выполняется, и момент сил

трения играет некоторую роль. В этом случае следует рассматривать вращающий момент как разность моментов создаваемых силой натя-

жения и силами трения M = Mн −M тр.

11

Порядок выполнения работы.

Задание 1.

1.Закрепить грузы на спицах вблизи оси вращения. Убедиться, что маятник находится в положении безразличного равновесия

2.Измерить высоту Н. С помощью штангенциркуля измерить радиус шкива, на который наматывается нить (R1 или R2).

3.Измерить время прохождения расстояния Н для изначально закрепленного на нити груза и с добавляемыми грузами, используя электронный блок. Измерения провести для нескольких грузов (нескольких моментов силы). Для каждого груза измерение времени проводить 3 – 5 раз.

Чтобы момент сил трения был постоянным, общая масса груза не должна быть больше 120 ÷ 130 г (масса закрепленного на нити груза равна 50 г)

Результаты измерений и результаты их последующей обработки поместить в таблицу.

Таблица 3.1

mi t1 t2 … ti tср a β Mн Mтр M

m1

…

m5

4.Вычислить величины a, β и Mн по формулам (3.1), (3.2) и

(3.3) соответственно для всех грузов.

5. Построить график зависимости Mн = I β+Mтр, откла-

дывая по вертикальной оси величину Mн , а по горизонталь-

ной оси величину углового ускорения β. Отрезок, отсекаемый прямой на оси ординат, равен моменту сил трения. Используя метод наименьших квадратов, вычислить тангенс угла наклона построенной прямой, который определяет момент инерции маятника I1.

12

Задание 2.

6.Сместить грузы на спицах маятника на концы спиц. Убедиться, что система находится в положении безразличного равновесия. Повторить такие же измерения, изменяя момент силы, действующей на маятник. Результаты поместить в таблицу аналогичную таблице 3.1. Полученные результаты обработать методом наименьших квадратов и нанести в таком же масштабе на предыдущий график. Вычислить момент инерции маятника I2.

Задание 3.

7.Грузы передвинуть и закрепить в середине спиц таким образом, чтобы маятник находился в положении безразличного равновесия. Все измерения и расчеты повторить, записать их в таблицу и построить график. Вычислить момент инерции маятника I3.

Задание 4.

8.На построенных графиках зависимости, β = f (M ) выбрать

три значения момента силы Mн Для каждого значения

M найти из графиков величины β1, β2, β3, соответствующие трем моментам инерции. Построить графики зависимости β = f ( 1I ) при M = const. Зависимости должны быть

линейными.

Внимание! Так как аналогичную работу можно выполнить, используя шкив другого радиуса, предварительно перемотав на него нить, то выполнение тех или иных пунктов заданий должно быть согласовано с преподавателем. Спрашивайте указания преподавателя!

Содержание отчета

1.Расчет величин линейного ускорения маятника a, углового ускорения β, вращающего момента Mн для всех грузов. Расчеты трех моментов инерции маятника. Моменты инер-

13

ции и их доверительные интервалы должны быть рассчитаны по методу наименьших квадратов.

2.Графики зависимости Mн = f (β) при I = const (три пря-

мые на одном графике) и зависимости β = f ( 1I ) при M = const (три прямые на другом графике).

Контрольные вопросы

В каких единицах измеряются угловое ускорение, угловая скорость, вращательный момент силы и момент инерции твердого тела?

Как определить момент инерции тела относительно данной оси, если известен момент инерции тела относительно оси, проходящей через центр инерции тела, параллельно данной оси?

Почему нельзя допускать раскачивания груза, подвешенного на нити, при его движении вниз? На что это будет влиять?

14

Тема: УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ

Введение.

Любое тело, находясь в гравитационном поле Земли, испытывает действие силы земного притяжения, которую можно выразить через закон всемирного тяготения:

F =G MRm2 ,

здесь G – гравитационная постоянная, M – масса Земли, m – масса тела, R – расстояние от центра Земли до тела. В случае, когда тело находится на поверхности Земли - R равно радиусу Земли.

Эта сила всем телам сообщает одно и то же ускорение - ускорение свободного падения g:

g = mF =G RM2 .

В данной точке вблизи земной поверхности ускорение свободного падения для всех тел, независимо от их массы, – величина постоянная. Однако в различных местах на земной поверхности g оказывается различным, что обусловлено несколькими причинами:

•Система отсчета, связанная с Землей является неинерциальной, следовательно, на все, находящиеся на ней тела, действует центробежная сила, причем эта сила зависит от широты. Нет ее только на полюсе, а на экваторе она максимальна.

•Земля сплюснута с полюсов. Тело, находящееся на полюсе, ближе к центру Земли, чем на экваторе.

•Принято за поверхность Земли считать поверхность, совпадающую со свободной невозмущенной поверхностью воды земных океанов. Однако, поверхность Земли неровная, и ускорение зависит от высоты места. Кроме того, под поверхностью может быть сложное распределение масс (горные породы сильно отличающейся плотности). Эти факторы приводят к вариациям силы тяжести.

Поверхность Земли имеет форму, которую принято называть геоидом, геоид близок к эллипсоиду вращения. Представляя Землю в виде такого эллипсоида и учтя центробежную силу, французский математик Клеро вывел формулу, выражающую зависимость ускорения силы тяжести от широты (теорема Клеро):

gϕ = gо(1+ 0.005302sin2ϕ ─ 0,0000059sin22φ)

здесь gо - значение ускорения силы тяжести на экваторе, равное 9.7803 м/сек2, gϕ - ускорение на широте ϕ.

15

Лабораторная работа №4

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ ОБОРОТНОГО МАЯТНИКА

Прежде, чем приступить к работе, необходимо ознакомиться с введением по теме «Динамика вращательного движения твердого тела» и «Ускорение свободного падения».

ЦЕЛЬ РАБОТЫ: определение ускорения свободного падения.

Физическое обоснование эксперимента

Физический маятник

Вращение твердого тела (см. введение) подчиняется закону:

M = I β ,

(4.1)

	где I - момент инерции тела, M - момент силы,	β =	∂2φ	- угловое
			∂t2
	ускорение.
	Физическим		маятником		на-
	зывается любое	твердое тело,			спо-

собное совершать колебания вокруг неподвижной оси, не проходящей через его центр инерции (центр масс).

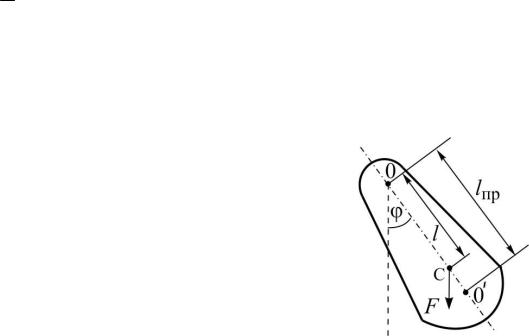
На рис. 4.1 точка O – проекция оси вращения на плоскость рисунка, точка С – центр инерции, пря-

мая ОО′, проходящая через точку С и О (перпендикулярная оси вращения) – ось маятника. l – расстояние от центра инерции до оси вращения. При отклонении маятника от поло-

Рис. 4.1 жения равновесия на угол φ возникает момент силы тяжести

16

M = r F , стремящийся вернуть маятник в положение равновесия.

Модуль этого момента равен M = mgl sin φ. Подставив его значение в уравнение (4.1), получим:

−mgl sin φ = I	d 2φ		(4.2)
	dt	2

Знак «–» стоит потому, что момент силы тяжести направлен так, что всегда возвращает маятник к положению равновесия.

Для малых углов (φ < 5°) справедливо соотношение: sin φ ≈ φ. Обозначив mglI = ω2 , получим уравнение:

d 2	φ	2	φ = 0
dt	2	+ω		(4.3)

Уравнение (4.3), описывающее движение физического маятника при малых углах отклонения, представляет собой дифференциальное уравнение незатухающих собственных гармонических колебаний с циклической частотой ω. Соответственно период его колебаний будет равен:

	T =	2π = 2π	I			(4.4)
			mgl
		ω
	Если сравнить это выражение с выражением для периода ко-
	лебаний математического	маятника	(T = 2π		l	), то видно, что
					g

роль, аналогичную длине l математического маятника, играет вели-

чина I . Эту величину называют приведенной длиной физического ml

Математическим маятником называется идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешено тело, с размерами много меньше длины нити l (материальная точка).

17

маятника.

Таким образом, приведенной длиной физического маятника называется длина математического маятника с периодом колебаний, равным периоду данного физического маятника. Тогда из формулы (4.4) легко получить:

	4π2l
g =	прив	(4.5)
	T 2

Отложим вдоль оси физического маятника от оси вращения (рис. 4.1) расстояние равное приведенной длине. Полученная точка О' называется центром качания. Она обладает тем свойством, что если маятник перевернуть и подвесить за центр качания, то период его колебаний относительно оси проходящей через эту точку будет таким же, как и относительно исходной оси.

Опираясь на это свойство, можно утверждать, что если периоды колебаний физического маятника относительно двух различных параллельных осей совпадают, то расстояние между ними равно приведенной длине физического маятника. На этом и основан используемый в данной работе метод (рис. 4.2).

Период колебаний маятника относительно одной оси –

T = 2π	I1	, а относительно второй – T = 2π	I2	. Здесь I1
1	mgl1	2	mgl2

и I2 - моменты инерции маятника относительно первой и второй осей, l1 и l2 – расстояния от центра инерции до двух осей, соответственно. По теореме Штейнера момент инерции тела относительно некоторой оси выражается через момент инерции I0 относительно оси, проходящей через его центр инерции и параллельный данной по формуле:

I = I0 +ml2, где l – расстояние между этими осями.

Тогда:

T = 2π	I	0	+ml2	T = 2π	I	0	+ml2
			1				2	(4.6)
1		mgl1		2		mgl2

Возведя эти уравнения в квадрат, и вычтя первое из второго, получим:

18

T 2mgl	2	−T 2mgl = 4π2m(l						2	−l2 )		(4.7)
2		1	1				2		1
			g =	4π2 (l2			−l	2 )			(4.8)
или						2	1
				T 2l	2	−T 2l
			2				1	1

Если периоды равны, т.е. T1=T2=T, то это уравнение преобразуется к виду

g =	4π2 (l	+l	2	)
	1				(4.9)
	T	2

что аналогично уравнению (4.5), т.к. (l1 + l2) в случае равенства периодов равно приведенной длине.

Описание экспериментальной установки.

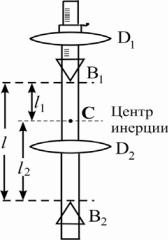
Физический маятник, используемый в данной работе, представляет собой массивный стержень, на котором укреплены две опорные призмы B1 и B2 и два дополнительных груза, выполненные в виде

«чечевиц» - D1 и D2. (Рис. 4.2.)

Опорные призмы предназначены для подвешивания маятника на специальную опору двумя способами (прямое и оборотное положение) и жестко закреплены на стержне. Расстояние между призмами измерено ранее при помощи высокоточного прибора и указано на рабочем месте. Одна из «чечевиц» жестко закреплена, другая может перемещаться вдоль стержня, причем ее положение можно определять по шкале.

При перемещении «чечевицы» изменяется момент инерции маятника, а, следовательно, и период его колебаний.

19

Для измерения периодов колебаний маятника используется частотомер, соединенный с фотоэлементом.

Фотоэлемент укреплен перед маятником, а за маятником – лампочка. В неподвижном положении маятник перекрывает свет, идущий от лампочки к фотоэлементу. При колебаниях маятника такое перекрывание осуществляется два раза за один период колебаний. Частотомер установлен в режим, при котором фиксируется время 10-ти прохождений маятника мимо фотоэлемента, т.е. 5-ти периодов.

Для определения центра инерции маятника служит на- Рис. 4.2 стольная призма, на которой маятник уравновешивается. Расстояние

от центра инерции до ближайшей опорной призмы измеряется линейкой.

Порядок выполнения работы.

1.Включить лампочку и частотомер.

2.Убедиться в том, что при отсутствии маятника свет от лампочки попадает на фотоэлемент.

3.Убедиться в том, что частотомер настроен на необходимый режим и срабатывает при перекрывании света (с помощью преподавателя или дежурного сотрудника лаборатории).

4.Закрепить подвижную «чечевицу» в некотором начальном положении. (Например, 4 см по шкале маятника).

5.Подвесить маятник на одну из опорных призм. Привести его в колебательное движение (угол отклонения не более 50). Измерить период колебаний Т1 (не менее 3 раз).

6.Не изменяя положение подвижной «чечевицы», перевернуть маятник и подвесить его на другой опорной призме. Изме-

20