ЛЕКЦИЯ 5

ДИСКРЕТНЫЙ КАНАЛ С ШУМОМ. ОСНОВНАЯ ТЕОРЕМА К. ШЕННОНА ДЛЯ ДИСКРЕТНОГО КАНАЛА С ШУМОМ.

ЦЕЛЬ ЛЕКЦИИ: Дать определение дискретного канала с шумом, рассмотреть особенности восстановления принятого сигнала при заданных надежности и пропускной способности канала. Выполнить доказательство основной теоремы для дискретного канала с шумом, привести примеры обеспечения максимальной пропускной способности дискретного канала с шумом.

Представление дискретного канала с шумом.

Когда в процессе передачи сигнал искажается шумом, принятый сигнал не обязательно совпадает с сигналом, посланным передатчиком. Можно выделить два случая. Первый, когда из определенного переданного сигнала всегда получается один и тот же принятый сигнал, и принятый сигнал является определенной функцией от переданного сигнала. Такое явление называется искажением. Если эта функция имеет обратную, т. е. никакие два переданных сигнала не создают один и тот же принятый сигнал, искажение может быть скорректировано путем выполнения обратной функциональной операции над принятым сигналом.

Второй, когда сигнал при передаче испытывает не всегда одинаковые βизменения. В этом случае можно считать, что принятый сигнал Е является функцией переданного сигнала S и второй переменной – шума N:

E = f(S,N). [1]

Шум рассматривается как случайная переменная, точно так же, как рассматривалось сообщение. В общем случае шум может быть представлен соответствующим стохастическим процессом. Наиболее общий тип дискретного канала с шумом является обобщением ранее описанного канала без шума с конечным числом состояний. Предположим, что число состояний конечно, и имеется множество вероятностей

P_α,i(β,j)

Это есть вероятность того, что, если канал находится в состоянии α и передается символ i, то будет принят символ j и канал перейдет в состояние β. Таким образом, α и β пробегают все возможные состояния, i – все возможные передаваемые сигналы, а j – все возможные принимаемые сигналы. В том случае, когда последовательно передаваемые символы искажаются шумом независимо, имеется только одно состояние и канал описывается множеством переходных вероятностей p_i(j) ( вероятностей того, что переданный символ i будет принят как j).

Если канал с шумом питается некоторым источником, то имеются два статистических процесса: источник и шум. Поэтому имеется несколько энтропий, которые могут быть вычислены. Во – первых, существует энтропия источника или энтропия входа канала H(x) ( они равны, если передатчик невырожденный). Энтропия выхода канала, т.е принятого сигнала, будет обозначена через H(у).Если шум отсутствует, H(х) = H(y). Совместную энтропию входа и выхода обозначим H(x,у). Наконец, имеются две условные энтропии H_x(y) и H_y(х) (энтропия выхода, когда вход известен, и обратно). Эти величины связаны соотношением

H(x,y) = H(x) + H_x(y) = H(y) + H_y(x). [2]

Все эти энтропии могут измеряться как энтропии на одну секунду или на один символ.

Надежность и пропускная способность канала.

В общем случае при наличии шума невозможно восстановить с полной определенностью исходное сообщение или переданный сигнал, применяя какую - либо операцию к принятому сигналу Е. Вместе с тем, имеются некоторые способы передачи информации, которые являются оптимальными в отношении борьбы с шумом.

Предположим, имеются два возможных символа 0 и 1, и мы ведем передачу со скоростью 1000 символов в секунду с вероятностями р₀ = р ₁ =1/2

Таким образом, источник создает информацию со скоростью 1000 бит/с. В процессе передачи шум вносит ошибки таким образом, что в среднем один из 100 символов принимается неправильно (0 вместо 1 или 1 вместо 0). Какова в данном случае скорость передачи информации? Ясно, что она меньше 1000 бит/c, так как около 1 % принятых символов неправильны. Кажущееся очевидным решение – вычесть средне число ошибок и получить результат 990 бит/c – не правильно, т. к. при этом не учитывается, что получатель не знает, где произошла ошибка. Если рассмотреть крайний случай и предположить, что шум настолько велик, что принятые символы полностью не зависят от переданных, то вероятность принять 1 или 0 равна 1/2, какой бы символ не был передан (0 или 1). Тогда около половины принятых символов будут правильными и следует считать, что скорость передачи составляет 500 бит/c. В этом случае не приходится говорить о передаче информации. Такой результат можно получить, подбрасывая монету в месте приема.

Очевидно, истинная поправка к количеству преданной информации равна той части этой информации, которая отсутствует в принятом сигнале или иначе, той неопределенности относительно переданного сигнала, которая имеет место, когда известен принятый сигнал. Опираясь на понятие энтропии как меры неопределенности, используем условную энтропию сообщения (при известном сигнале) как меру этой недостающей части информации. Такое определение является подходящим, поскольку было бы можно получить скорость действительной передачи информации R, вычитая из скорости создания информации (энтропии источника) среднюю скорость условной энтропии

R = H(x) – H_y(x) [3]

Назовем условную энтропию H_у(x) ненадежностью, считая, что она является мерой средней неопределенности принятого сигнала.

В рассматриваемом нами примере прием символа 0 означает, что апостериорная вероятность того, что был принят символ 0, равна 0,99, а того, что была передана единица – 0,01. Если же была принята единица, имеем обратную картину. Следовательно, ( 5 – е свойство энтропии)

H_у(x) = -[0,99log0,99 + 0,01log0,01] = 0,081 бит/символ.

Для заданной скорости это составит 81 бит/с. Таким образом, в соответствии с [3] система передает информацию со скоростью 1000 – 81 = 919 бит/с. В крайнем случае, когда при передаче символа 0 равновероятен прием как 0, так и 1 (аналогично для символа 1), апостериорные вероятности равны соответственно 1/2 и 1/2. Тогда

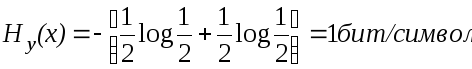
В этом случае скорость передачи равна 0, как следует из [3].

Р

Источник

Передатчик

Приемник

Корректирующее устройство

Наблюдатель

Коррекционный сигнал

М

М’111ё

М

ассмотрим систему связи и наблюдателя, который может видеть, как то, что передается, так и то, что принимается с ошибкой из-за шума. Этот наблюдатель отмечает ошибки в принятом сообщении и передает эти данные в точку приема через “коррекционный канал”, чтобы дать возможность в точке приема исправить ошибки.

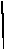
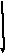
Схема показана на рис. 1

Рис. 1 Схема корректирующей системы.

ТЕОРЕМА. Если коррекционный канал имеет пропускную способность, равную H_у(x), то можно так закодировать данные коррекции, чтобы их можно было передавать по этому каналу и корректировать все ошибки, за исключением произвольно малой доли ε этих ошибок. Это невозможно, если пропускная способность коррекционного канала меньше чем H_у(x).

Или иначе, H_у(x) есть количество дополнительной информации, которая должна передаваться в точку приема за одну секунду для исправления принятого сообщения.

Для доказательства рассмотрим длинные последовательности принятых сообщений М’ и соответствующие исходные сообщения М. Для каждого из сообщений М’ среди сообщений М будут иметься (с логарифмической точностью) ТН_у(х) сообщений, из которых оно могло бы быть по существу создано. Поэтому требуется передавать каждые Т секунд ТН_у(х) бит. Это может быть осуществлено с частотой ошибок ε при помощи канала с пропускной способностью Н_у(х).

Вторую часть теоремы можно доказать, если заметить, что для любых дискретных случайных переменных x,y,z

H_y(x,z) ≥ H_y(x)

Разложив левую часть, получим

H_y(z) + H_yz(x) ≥ H_y(x),

H_yz (x) ≥ H_y(x) – H_y(z) ≥H_y(x) – H(z). [4]

Ecли отождествлять х с выходным сигналом источника, у с принятым сигналом и z с сигналом, посланным по коррекционному каналу, то правая часть равна ненадежности за вычетом скорости передачи по коррекционному каналу. Если пропускная способность коррекционного канала меньше ненадежности, то правая часть выражения [4] будет больше нуля и H_yz(x)>0. Но это выражение есть неопределенность того, что было передано при известном принятом сигнале и корректирующем сигнале. Если эта неопределенность больше нуля, то частота ошибок не может быть сделана произвольно малой.

Рассмотрим следующий пример. Предположим, что в двоичной последовательности ошибки происходят случайным образом: вероятность того, что символ неправильный, равна р и вероятность того, что символ правильный, q = 1 – p. Эти ошибки могут быть исправлены, если известны их положения. Таким образом, по коррекционному каналу нужно посылать информацию только об их позициях. Это сводится к передаче информации от источника, который создает двоичные цифры, причем 1 имеет вероятность р (неправильно) и 0 – вероятность q (правильно). Для этого требуется канал с пропускной способностью

- [p log p+ q log q],

что равно ненадежности исходной системы.

Исходя из тождества [2], скорость передачи R [3] можно записать как

R = H(x) – H_y(x) = H(y) – H_x(y) = H(x) + H(y) – Н(x,y). [5]

Первое из этих выражений соответствует [3] (количество информации минус неопределенность того, что было послано). Второе выражение является мерой количества принятой информации минус та ее часть, которая обусловлена шумом. Третье выражение есть сумма этих двух количеств минус совместная энтропия, и поэтому оно в некотором смысле представляет число бит в секунду, общее этим двум количествам. Таким образом, выражения имеют определенный интуитивный смысл.

Пропускная способность канала с шумом должна быть максимально возможной скоростью передачи, т. е. скоростью при надлежащем согласовании источника с каналом. Поэтому определим пропускную способность канала как

C = max[H(x) – H(y)], [6]

где максимум берется по всем возможным источникам информации, используемым в качестве входа в канал Если рассматривается канал без шума, то H(x) = 0. Тогда это определение эквивалентно уже данному ранее определению канала без шума, так как по теореме об энтропии канала максимум энтропии для канала равен его пропускной способности.