Лекции / ЛЕКЦИЯ 1.doc Информационный аспект

ЛЕКЦИЯ 1

ИНФОРМАЦИОННЫЙ АСПЕКТ ПРОБЛЕМЫ ПРЕДСТАВЛЕНИЯ ДАННЫХ ДЛЯ ПЕРЕДАЧИ ПО КАНАЛУ.

ЦЕЛЬ ЛЕКЦИИ: Исходя из требований к линии связи, дать основные термины и определения теории информации и рассмотреть свойства энтропии случайной дискретной величины.

“Многие вещи нам непонятны не потому, что наши понятия слабы;

но потому, что сии вещи не входят в круг наших понятий”.

Козьма Прутков.

В 1948 году американский ученый К. Шеннон (скончался в феврале 2001 года) опубликовал ставший знаменитым труд ”Математическая теория связи”, послуживший базой для развития теории информации. Считается, что К.Шеннон является основоположником цифровой связи. Поскольку методы цифровой обработки сигналов получили широкое распространение в различных областях техники, знание основных положений теории информации является необходимым для специалиста в области цифровых технологий и телекоммуникационных систем в частности.

Основные термины и определения.

Система связи. Система связи должна быть спроектирована так, чтобы ее можно было использовать для передачи любого возможного сообщения (из множества возможных), а не только того, которое в действительности будет выбрано, так как результат этого выбора неизвестен в момент проектирования. Общая схема системы связи представлена на рис.1.

Источник информации

Передатчик

Приемник

Адресат

Источник шума

Сообщение

Сигнал

Принятый сигнал

Сообщение

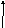
Рис. 1 Общая схема системы связи.

Источник информации. Источник информации, создает сообщение или последовательность сообщений, которые должны быть переданы на приемный конец. Сообщения могут быть различных типов: функции времени, случайные дискретные последовательности, функции одной или нескольких переменных и т. д.

Передатчик. Передатчик перерабатывает некоторым образом сообщение в сигналы, соответствующие характеристикам данного канала.

Канал. Канал – это среда, используемая для передачи сигналов от передатчика к приемнику.

Замечание: здесь и далее канал определяется как соединение “точка – точка” в линии связи, поскольку среда может обеспечить многоканальную передачу.

Приемник. Приемник выполняет обычно операцию, обратную к операции, производимой передатчиком, восстанавливая сообщение по сигналам.

Адресат. Адресат – лицо или аппарат, которому предназначено сообщение.

Системы связи можно разделить на следующие категории:

- дискретные, под которыми будем понимать системы, в которых сообщение и сигнал являются случайными последовательностями дискретных символов (телеграф, компьютерные сети, ..).

- непрерывные, системы, в которых сообщение и сигнал рассматриваются как непрерывные функции (радио, телевидение,…).

- смешанные, такие, как цифровая телефония.

В данной части курса будет рассматриваться только дискретная система. В процессе изучения материалов курса придется оперировать терминами, определение которых дано ниже.

Бит: 1,0. Введен в обращение американским ученым-статистиком Д. Тьюки в 1946 году.

Алфавит– множество различных символов, порождаемых источником.

Размер алфавита – количество символов.

Символ – единица некоторого языка (буквы, цифры, ноты и т.д.).

Код – конечная последовательность битов.

Длина кода – количество битов в нем.

R – битовый элемент - совокупность битов – имеет 2^К возможных значений – состояний.

Байт – 8 бит.

Слово – конечное число элементов.

Длина слова – количество элементов.

Сигнал – изменяющийся во времени физический процесс, отражающий передаваемое сообщение. Сигнал всегда является функцией времени.

Сообщение – информация, представленная в форме сигнала или совокупности сигналов.

Источник данных порождает поток либо содержит блок данных. Вероятности порождения элементов определяются состоянием источника. У источника без памяти – одно состояние, у источника с памятью – множество.

Источник без памяти порождает “элементы”.

Источник с памятью порождает “слова”.

Источник Бернулли – бинарный источник без памяти.

Источник Маркова – источник с памятью (состояние на i – м шаге зависит от состояний на N предыдущих шагах).

При изучении основ теории информации нам придется постоянно обращаться к основным понятиям и положениям теории вероятностей. Поэтому уместно вспомнить основные из них.

Основные понятия и определения теории вероятностей.

Теория вероятностей представляет исследователю понятийный и математический аппарат для описания случайных событий.

Явления, исход которых не может быть однозначно определен до того, как они произошли, называются случайными. Количественное описание случайных событий базируется на том, что при многократном повторении явления с неоднозначным исходом в одних и тех же условиях частота появления некоторого результата остается приблизительно одинаковой.

Опыт – любая совокупность условий и воздействий, при которых происходит интересующее нас событие.

Событие – исход опыта, результат наблюдения.

Пусть нас интересуют только благоприятные исходы M некоторого числа опытов N. Тогда отношение M/N покажет долю благоприятных исходов или относительную частоту их появления. Проведем серию опытов. При малом количестве опытов в серии численные значения этой частоты могут существенно отличаться от серии к серии. Пример – три серии по три бросания монеты. Если увеличивать число опытов в серии, устремив его в бесконечность, увидим, что частота благоприятных исходов будет сколь угодно близко приближаться к определенной постоянной величине. Запишем эту операцию математически

P(A) = lim M/N при N

Величина p(A) называется вероятностью случайного события А. Иными словами, вероятность случайного события есть количественное выражение степени возможности события. Приведенное определение вероятности является частотным. Оно применимо для возможных исходов, образующих дискретный набор, и будет основным при изучении материалов курса.

Если все возможные исходы равновероятны, то вероятность любого из них равна p = 1/n. (Бросание монеты: n = 2, p = 1/2).

Если благоприятное событие реализуется несколькими способами (m) из n равновероятных, p = m/n. ( m n).

Пример: выпадение четной цифры при бросании игральной кости n = 6, m = 3.

В ящике 10 шаров: 5 зеленых, 3 красных,2 синих. Вероятность вынуть красный шар p_К = 0,3 (n = 10, m = 3).

Свойства вероятности.

1. Вероятность есть следствие случайного события, т. е. можно считать, что вероятность является функцией события p = p( A ).

2. Достоверное событие – событие, которое обязательно происходит. Вероятность достоверного события равна 1. Все другие события (возможные, но не достоверные) имеют вероятность меньше 1. Из этого положения следует условие нормировки вероятностей

0 ≤ p_А ≤ 1. [ 1 ]

3. Правило сложения вероятностей.

Полагаем, что среди возможных вероятных исходов благоприятным оказывается любое из событий А или B. При этом A и B – независимы (между ними отсутствуют причинно- следственные связи – А не влияет на В и наоборот) и несовместны (то есть, они не могут наступить одновременно, а наступает всегда лишь одно из них). Пусть из общего числа n равновероятных исходов событие А осуществляется m₁ числом способов, а событие В – m₂. Тогда

p_А = m₁ / n , а p_В = m₂ / n.

Как найти вероятность события С = ( А или В ) (в обозначении алгебры логики С = А В )? Число способов, которым может реализоваться событие С, равно m₁ + m₂. Следовательно,

P_AB = (m₁ + m₂) / n = m₁ / n + m₂ /n = p_A + p_B.

Вероятность какого- либо одного из двух исходов независимых и несовместных событий равна сумме их вероятностей.

P_{A B} = p _A + p_B. [ 2 ]

Вероятность вынуть синий и зеленый шары (см. пример) р_с٧з = 0,2 + 0,5 = 0,7. Эту формулу можно обобщить на произвольное число благоприятных исходов. Если при n равновероятных исходах k несовместных событий являются благоприятными, причем, вероятности каждого из них составляют p₁ , p₂ , … , p_k , то вероятность наступления любого (хотя бы одного) из благоприятных событий будет равна

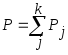[ 3 ]

Из двух последних соотношений и условия нормировки вероятностей выводятся два следствия.

Следствие 1. Если общее количество всех возможных исходов равно n с вероятностями p₁, ….p_n, то

поскольку появление хоть какого – то из исходов достоверно. Выражение является обобщенным условием нормировки.

Следствие 2. Если возможных исходов два (А или В), то наступление одного означает не наступление второго. Такие исходы называются противоположными.

Это условие записывается таким образом

Если p_A + p_B = 1 и p_B = 1 – p_A , то

[ 4 ]

Если вероятность вынуть синий или зеленый шар 0,7, то вероятность не вынуть любой из них равна 1-0,7 = 0,3.

4. Умножение вероятностей.

Рассмотрим два опыта. В первом событие А реализуется m₁ способами из n₁ равновероятных исходов. Во втором событие В реализуется m₂ способами из n₂ равновероятных исходов. Опыты независимы. Какова вероятность одновременного наступления обоих событий (сложного события С, определяемого наступлением и А и В)? Событие С в таком случае называется совместным: С = А ^ В.

Поскольку каждому из n₁ исходов первого опыта соответствует n₂ исходов второго, то общее количество возможных равновероятных исходов равно произведению n₁ x n₂ . Из них благоприятными окажутся m₁ x m₂ исходов. Следовательно, вероятность совместного события оказывается равной :

P_А^В = m₁ х m₂/n₁ · n₂ = m₁/n₁ х· m₂/n₂ = p_А х· p_В.

Вероятность одновременного наступления двух исходов независимых событий равна произведению их вероятностей.

p_А^В = p_А х· p_В. [ 5 ]

Пример. Какова вероятность выпадения “6” при однократном бросании двух игральных костей? p_A = p _B = 1/6, p = 1/6 x 1/6 = 1/36.

Проведем обобщение для произвольного числа совместных благоприятных событий в k независимых опытах. Если вероятности их наступления в каждом из опытов p₁, p₂,…,p_k, то вероятность совместного события будет равна:

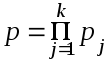
Следствие 3. Поскольку p_j 1, очевидно, что p p_j, т.е. вероятность совместного события не может превышать вероятность любого из них.

Следствие 4. Нахождение среднего для значений случайных величин. Пусть в частной ситуации случайным событием является числовое значение некоторой величины. Пример – число на грани игральной кости. Пусть этих значений n и они образуют дискретный ряд x₁, x₂, . . . , x_n . Среди этих значений могут оказаться одинаковые. Если таких групп одинаковых значений k, то очевидно, что k n. Каково же среднее значение величины x? Пример: Сколько очков выпадет при одном броске игральной кости? Исходя из определения среднего значения, имеем

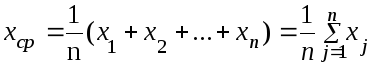
Эта же сумма может быть получена, если провести суммирование по группам одинаковых значений:

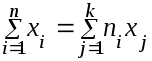
здесь n_j – количество значений в группе j. Тогда

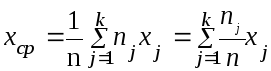
поскольку отношение nj/n есть относительная частота появления результата из группы j, которая в пределе превращается в вероятность p_j , можем записать

Полученное соотношение называется взвешенным средним для выборки x₁, x₂, . . . , x_n.

Пример: Для броска игральной кости вероятность появления любого из чисел равна 1/6, а значения 1, 2, 3, . . . ,6. Определим взвешенное среднее для выборки из 6.

x_ср = 1/6 x ₁ + 1/6 x ₂ + 1/6 x ₃ + 1/6 x ₄ + 1/6 x ₅ + 1/6 x ₆ =

1/6(1 + 2 + 3 + 4 + 5 + 6) = 3,5.

Энтропия как мера неопределенности.

Утверждение. Если множество возможных сообщений конечно, то число сообщений или любую монотонную функцию от этого числа можно рассматривать как меру информации, создаваемой выбором одного сообщения из этого множества в предположении, что все сообщения равновероятны. Рассмотрим возможности выбора и неопределенности подробнее.

Пусть имеется ансамбль или некоторое множество возможных исходов опыта, вероятности осуществления которых нам известны и составляют соответственно p₁, p₂, . . . , p _n. Зададимся вопросом: возможна ли мера того, какое событие произойдет? Насколько велик “выбор” из данного множества или какова неопределенность его исхода?

Предположим, такая мера H(p₁. p₂, . . . , p _n) имеется, причем он должна обладать следующими свойствами:

1. H должна быть непрерывной относительно p_i.

2. Если все p_i равны, p_i = 1/n, то H должна быть монотонно возрастающей функцией от n. В случае равновероятных событий имеется больше возможностей выбора или неопределенности, чем в случае, когда имеются события с различными вероятностями.

3. Если бы выбор распался на два последовательных выбора, первоначальная Н должна была бы быть взвешенной суммой индивидуальных значений Н.

Проиллюстрируем это рисунком.

1/2

1/2

1/2

1/3

2/3

1/3

1/2

1/3

1/6

1/6

Рис.1 Выбор из трех возможностей (слева) и из двух возможностей (справа).

На левом рисунке представлены три возможности выбора с вероятностями p₁ = 1/2, p₂ = 1/3, p₃ = 1/6. Справа производится выбор между двумя возможностями, причем каждая имеет вероятность 1/2. В случае осуществления второй возможности производится еще один выбор между двумя возможностями с вероятностями 2/3 и 1/3. Окончательные результаты имеют те же самые вероятности, что и прежде. Потребуем в данном конкретном случае, чтобы Н(1/2, 1/3, 1/6) = H(1/2, 1/2) + 1/2H(2/3, 1/3). Последнее условие можно охарактеризовать как условие аддитивности. Коэффициент 1/2 является весовым множителем. Он введен из-за того, что второй выбор осуществляется только в половине всех случаев.

ТЕОРЕМА. Существует единственная функция Н, удовлетворяющая трем перечисленным выше свойствам. При этом Н имеет вид

где К – некоторая положительная константа.

Выполним доказательство данной теоремы при условии, что можно разбить выбор из s^m равновероятных возможностей на m выборов из s равновероятных возможностей в каждом выборе.

Пусть H = (1/n, 1/n, . . . ,1/n.) = A (n). В соответствии с принятым условием должно выполняться равенство

A (s ^m) = m A (s).

Для равновероятных t ⁿ возможностей так же имеем

A (t ⁿ) = n A (t).

Определим m из условия

s ^m t ⁿ s^{(m + 1)}

Взяв n произвольно большим, прологарифмируем последнее выражение

m log s n log t (m + 1) log s

Разделив полученное на n log s, имеем

m / n log t / log s (m + 1) / n

Частное (m + 1) / n произвольно мало при n . Обозначим частное ε.

Тогда модуль разности m / n – log t / log s представляет собой малую величину, т. е.

!m / n – log t / log s! ε.

Используя второе условие, свойство монотонности A (n), можем записать

A (s ^m) A (t ⁿ) A [(s ^{( m + 1 )} ],

т.е. предполагаем, что после некоторого числа выборов значение неопределенности выбора A (t) оказалось в интервале [s ^m, s ^{m + 1}] выбора значений неопределенности A (s).

Вновь воспользуемся условием разбиения выбора из s^m равновероятных возможностей на m выборов из s равновероятных возможностей. Запишем

m A (s) nA (t) (m + 1)A (s).

Разделим полученное выражение на n A (s)

m / n A (t) / A (s) (m + 1) / n

Перепишем ! m / n – A (t) / A (s)! ε

Выполнив суммирование левых и правых частей полученных неравенств е, имеем

m / n – log t / log s + m / n – A (t) / A (s) 2ε

или - log t / log s – A (t) / A (s) 2ε – 2m / n.

Полагая правую часть неравенства равной нулю и умножив левую часть неравенства на A ( s ), получим

• log t A (s) / log s – A (t) = 0.

Полагая A (s)/log s = K , имеем

A (t) = - K log (t).

Вполне очевидно, что K положительно и растет с ростом s.

Расширим класс рассматриваемых ситуаций. Допустим. имеется выбор из n возможностей с соизмеримыми вероятностями p_i = n _I / Σ n _{i ,}

где n – целые числа. Разобьем выбор из Σn _I возможностей на выбор из возможностей с вероятностями p₁, p₂, . . . , p _n с последующим равновероятным выбором из n _i возможностей, если в первом случае выбрано i. Пользуясь условием аддитивности приравняем полные неопределенности выборов из n _I , сосчитанные двумя способами:

K log Σ n _I = H(p₁, . . . , p _n) + KΣ p_i log n _i

Решив уравнение, получим

H = K [Σp_i log Σn _i –Σp_i log n _i ] =

= - KΣ p _i log n _i / Σ n _i = - KΣ p_i log p_i.

Выбор коэффициента K производится из соображений удобства: им определяется единица измерений.

Таким образом, выражение для функции Н справедливо и в общем случае:

H = - Σ p _i log p _i

Форма величины H оказывается такой же, как и форма энтропии, определяемой в статистической механике, где p – вероятность того, что система находится в ячейке i фазового пространства

На рисунке представлен график энтропии для случая двух возможностей в виде функции от p.

Рис. 2 Энтропия в случае двух возможностей с вероятностями p

и q = (1 – p).

График наглядно иллюстрирует функциональную зависимость вероятностей двух исходов, описываемую выражением

H = - (p log p + q log q)

Необходимо отметить одно важное обстоятельство, которое следует помнить при дальнейшем обсуждении темы. При изучении раздела мы определили величину H = - p_i log p_i как энтропию множества вероятностей p ₁, p ₂, . . . , p _n.

Если x – случайная величина, то ее энтропия обозначается через H (x). В данном случае x – не аргумент функции, а только знак, отличающий энтропию случайной величины x от энтропии H (y) случайной величины y.

Рассмотрим другой подход к выводу определения энтропии как меры неопределенности.

Пусть в некотором опыте A имеется n равновероятных исходов. Очевидно, что неопределенность каждого из них зависит от n. Запишем это положение в виде функции:

Неопределенность = f (n) .

Очевидны некоторые свойства этой функции:

1. f (1) = 0 , так как при n = 1 событие достоверно, исход опыта не является случайным и, следовательно, неопределенность отсутствует.

2. f (n) возрастает с ростом n, так как при большом числе возможных исходов предсказание результата опыта становится затруднительным.

Перечисленных свойств функции недостаточно для определения вида функции. Дополним перечень свойств функции свойством аддитивности. Рассмотрим два независимых опыта A и B . В опыте А количество равновероятных исходов n _a, в опыте B, соответственно n _b. Пусть одновременное выполнение опытов A и B образует сложный опыт C. Число возможных исходов опыта равно произведению n _a n _b, причем все они равновероятны. Неопределенность исхода такого опыта будет больше неопределенности опыта А, поскольку к ней добавляется неопределенность опыта В. Допустим следующее: мера неопределенности опыта С равна сумме неопределенностей опытов А и В, т. е.