Лекции / ЛЕКЦИЯ 4

ЛЕКЦИЯ 4

СТАТИСТИЧЕСКОЕ КОДИРОВАНИЕ.

ЦЕЛЬ ЛЕКЦИИ: Продемонстрировать практическое применение положений “Теории информации” на примерах сокращения избыточности текста построением кодов Шеннона – Фано и Хаффмана.

В предыдущих лекциях были рассмотрены энтропия источника сообщений, общие вопросы кодирования сообщений, показано, что относительная энтропия источника, оперирующего определенным алфавитом символов, характеризует степень сжатия, достижимую при использовании данного алфавита. На базе полученных представлений о свойствах дискретного источника сообщений рассмотрим некоторые подходы к уменьшению избыточности информации при статистическом кодировании.

Несколько слов о терминологии. Источник производит сообщение в виде последовательности символов a. Каждый символ последовательности может принять одно из M значений а_j (1 j M). В простейшем случае каждое значение символа а_j в кодирующем устройстве обозначается некоторой кодовой комбинацией. Эта комбинация представляет собой последовательность из n_j знаков, каждый из которых может принять одно из m значений. Общепринята следующая терминология:

n_j – длина или значность кодовой комбинации;

m – основание кода.

Совокупность кодовых комбинаций, соответствующих всем значениям кодируемых символов а_j, составляет код. Важной характеристикой кода является его структурная функция G(j), определяющая число кодовых комбинаций длительностью n_j. Ниже приведены кодовые обозначения кодируемых символов и структурная функция кода.

Кодируемые символы / кодовые обозначения

а₁ / 1 ; a₂ / 01; a₃ / 001; a₄ / 0001; a₅ / 0000

! 1 при n_j = 1

G(j) = { 1 при n_j = 2

! 1 при n_j = 3

! 2 при n_j = 4

Код, у которого структурная функция отлична от нуля только в одной точке, называется равномерным. Равномерные коды находят применение, главным образом, при передаче сообщений по каналам с шумом и помехами. Коды, у которых структурная функция отлична от нуля в двух и более точках, называются неравномерными кодами. Эти коды используются реже, чем равномерные. Их применяют, в основном, с целью сокращения длины кодируемого сообщения.

Устройство, осуществляющее операцию кодирования, называется кодирующим устройством. Его можно представить в виде устройства, которое в соответствии со значением кодируемого символа определяет строку кодовой таблицы и посылает в канал кодовую комбинацию. Построенное таким образом кодирующее устройство должно хранить в памяти всю кодовую таблицу. При большом числе кодируемых символов оно оказывается достаточно сложным. Образованная в результате кодирования неравномерная во времени последовательность знаков кодовых комбинаций превращается с помощью упругой задержки в равномерную во времени последовательность знаков.

Рассмотрим источник, содержащий алфавит из четырех символов: а₁, a₂, a₃, a₄. Кодируемым символам соответствуют кодовые сообщения, приведенные в таблице.

Кодируемые символы	а1	а2	а3	а4
Кодовые сообщения	10	100	01	011

Источник сообщений произвел некоторую последовательность символов а₁, a₃, a₁, a₄, a₄, a₄, a_3, a ₁. В результате кодирования последовательность знаков на выходе кодирующего устройства примет вид: 1001100110110110110… Выполним операцию декодирования данной последовательности. Сопоставив комбинации кодовых обозначений, приведенных в таблице, увидим, что возможны два варианта декодирования первого символа: a₁ или а₂. Если первым символом является символ а₁, то следующим может быть либо а₃, либо а₄. Если же первым символом будет символ а₂, то декодирование следующего символа невозможно, поскольку кодовых комбинаций, начинающихся знаками 11 в кодовой таблице нет. Декодируя таким образом всю последовательность, восстановим первоначальную последовательность символов.

Код называется разделимым, если любую последовательность можно однозначным образом восстановить после операций кодирования и декодирования, использующих этот код.

Условие разделимости кода фактически сводится к требованию, чтобы никакая последовательность кодовых комбинаций данного кода не совпадала бы с другой последовательностью кодовых комбинаций этого кода. Проверить условие разделимости кода можно с помощью искусственного приема, воспользовавшись операцией тестирования. Выпишем все кодовые комбинации в первый столбец таблицы, приведенной ниже.

1	2	3	4	5	6
10	0	1	0	1	0
100	1	11	00	11	00
01		0	1	0	1
011		00	11	00	11

Если какая–либо из комбинаций в первом столбце является началом других комбинаций в этом столбце, то оставшуюся часть комбинации выписываем в столбец 2. В рассматриваемом примере комбинация 10 является началом комбинации 100, а комбинация 01 – началом комбинации 011. Поэтому в столбец 2 записываются остатки 0 и 1. Если какая-либо из комбинаций в столбце 2 является началом комбинации в столбце 1 или наоборот, то оставшуюся часть комбинации выписываем в третий столбец. Заполнение последующих столбцов производится аналогичным образом. Процесс продолжается до появления пустого столбца, либо до появления повторяемости столбцов.

В рассмотренном нами примере при декодировании первой кодовой комбинации оказалось необходимым проанализировать первые пять знаков последовательности, т. е. дополнительно три знака сверх двух знаков, входящих в комбинацию. В процессе дальнейшего декодирования число анализируемых знаков постоянно изменяется.

Интерес представляет наибольшее число анализируемых знаков, так как оно определяет требование к емкости памяти декодирующего устройства. Это число называют задержкой декодирования. Задержка декодирования может быть конечной и бесконечной. Тест, которым мы оперировали, выясняя разделимость кода, позволяет определить, является ли задержка декодирования конечной или бесконечной. Задержка декодирования является конечной, если какой-либо из столбцов таблицы, построенной в соответствии с приведенным тестом, оказывается пустым. Пример разделимого кода с конечной задержкой приведен в таблице.

Кодируемый символ

а1

а2

а3

а4

а5

а6

Кодовое сообщение

0 0 001

0010

0011

00101

00110

00100

Для этого кода тест на разделимость приводит к таблице, у которой четвертый столбец (а, следовательно, и последующие) оказывается пустым.

1	2	3	4
001		11, 010
0010	0	011, 0101
0011	1	0110,0100
00101	01	1, 10, 11
00110	10	101, 110
00100	00	100

Из необходимого и достаточного условия разделимости вытекает следующее простое требование: никакая кодовая комбинация не должна являться началом другой комбинацией того же кода. При выполнении данного требования, являющегося достаточным условием разделимости, в таблице, построенной в соответствии с тестом на разделимость, все столбцы, кроме первого, оказываются пустыми.

Коды, для которых выполняется последнее требование, называются кодами, обладающими свойствами префикса.

Эти коды характеризуются задержкой декодирования, равной длине наибольшей кодовой комбинации.

Префиксом кодовой комбинации называют саму комбинацию и комбинации, полученные из данной путем вычеркивания последних знаков.

Например, кодовая комбинация 011001110 имеет префиксы:011001110; 01100111; 0110011; 011001; 01100; 0110; 011; 01; 0. Код обладает свойством префикса в том случае, если никакая комбинация данного кода не является префиксом другой комбинации этого же кода. Иногда это свойство называют неприводимостью кода. Коды, обладающие свойством префикса, составляют обширный и важный класс кодов, включающий, в том числе, и равномерные коды. Для наглядного описания кодов, характеризующихся свойством префикса, используется способ кодового дерева. Дерево – это граф, состоящий из узлов и ветвей, соединяющих узлы. Узлы располагаются на отдельных уровнях. На начальном уровне находится один узел – корень. На первом уровне находится m узлов, на втором – m и на j-м уровне – m узлов. Полагается, что m и j – целые числа. Узел на уровне j соединяется ветвями с m узлами на уровне m + 1. Причем узел на уровне j +1 соединяется только с одним узлом на уровне j. На рисунке показано дерево, соответствующее значению m = 2.

Корень

0

1

0

1

0

1

0

1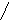

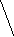
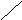
Каждая ветвь дерева, соединяющая узел на уровне j с m узлами на уровне j + 1, получает соответствующее обозначение в виде одного из m значений знака кодовой комбинации. При этом обозначения всех упомянутых ветвей различны. Каждый узел дерева получает кодовое обозначение. Для определения этого обозначения двигаемся от корня дерева к узлу, выписывая при этом обозначения пройденных ветвей. Полученная последовательность обозначений ветвей будет кодовым обозначением узла. Узлы, которые не соединяются ветвями ни с одним узлом, находящимся на следующем уровне, называются оконечными.

Узлы, соответствующие комбинациям кода, обладающего свойством префикса, являются оконечными.

Если к кодовым комбинациям кода нельзя добавить новой кодовой комбинации, не нарушив при этом свойства префикса, то код называется полным.

Кодовое дерево, соответствующее некоторому коду, может рассматриваться как ключ для декодирования сообщения, закодированного этим кодом. Процесс декодирования заключается в следующем. По мере приема информации совершается движение из узла на уровне j кодового дерева в новый узел на уровне j + 1 по ветви, обозначение которой совпадает с принимаемым знаком. При этом движение при приеме первого знака начинается от корня кодового дерева. Всякий раз при достижении оконечного узла отмечается прием кодовой комбинации, являющейся кодовым обозначением этого узла. Последующее декодирование начинается снова с корня кодового дерева. Таким образом , декодируемая последовательность знаков разбивается на последовательность кодовых комбинаций, которые затем преобразуются в последовательность символов сообщения. Нужно ли при таком декодировании кодовой комбинации знать последовательность знаков от ее начала и до декодируемых символов включительно? Оказывается, в ряде случаев необходимо знание лишь небольшого числа знаков, предшествующих декодируемой комбинации.

Если в качестве ключа для декодирования сообщения используется кодовое дерево, соответствующее полному коду, обладающему свойством префикса, то любая последовательность знаков будет декодироваться как начало некоторого сообщения. В случае неполного кода процесс декодирования некоторых последовательностей может заходить “в тупик”.

Рассмотрим еще один код – неравномерный систематический код, обладающий свойством префикса.

Неравномерный систематический код, обладающий свойством префикса, строится на основе некоторого исходного кода, также обладающего свойством префикса.

Комбинации исходного кода произвольным образом делятся на две группы: на элементарные и конечные комбинации. Кодовые комбинации систематического кода (он содержит бесконечное число таких комбинаций) представляют всевозможные последовательности элементарных комбинаций, оканчивающихся одной из конечных комбинаций. Пусть исходный код состоит из четырех кодовых комбинаций вида 0, 10, 110, 111. Примем в качестве элементарных комбинаций комбинации вида 0, 10, 110, а в качестве конечной комбинации – комбинацию 111. Тогда начальными кодовыми комбинациями систематического кода будут комбинации а₁ - 111, а₂ - 0111, а₃ – 10111, а₄ - 110111 … и т. д.

Предположим, что последовательность знаков, соответствующая сообщению, закодированному некоторым систематическим кодом с одной конечной комбинацией, обладающим свойством префикса, подается на линейный фильтр, ”настроенный” на конечную кодовую комбинацию. Если в качестве конечной кодовой комбинации принята, например, комбинация 1100, то всякий раз, когда последний знак кодовой комбинации систематического кода поступает на вход первого элемента задержки, на выходе фильтра появляется величина, равная значности конечной кодовой комбинации рассматриваемого кода. Можно построить коды, при применении которых фильтр, настроенный на одну или несколько комбинаций, может использоваться для определения конца кодовой комбинации. Такие коды называются кодами с разделительным знаком. Структурные особенности этих кодов существенно зависят от выбора разделительного знака, в качестве которого может быть взята одна или несколько комбинаций.

Необходимо отметить существенное отличие кодов с разделительным знаком от других кодов, обладающих свойством префикса. Отличие заключается в следующем. При использовании кодов, обладающих свойством префикса, в общем случае для декодирования данной кодовой комбинации необходимо знать либо всю последовательность знаков от начала до декодируемых знаков включительно, либо в ряде случаев значительный отрезок этой последовательности, предшествующий декодируемой кодовой комбинации. В случае применения кодов с разделительным знаком для декодирования данной кодовой комбинации достаточно с помощью фильтра, “настроенного” на комбинацию, обозначающую разделительный знак, выделить отрезок последовательности. Выделенный отрезок должен заключаться между двумя соседними моментами, когда величина на выходе фильтра совпадет со значностью комбинации, служащей разделительным знаком. По выделенному отрезку последовательности знаков можно однозначно восстановить переданную кодовую комбинацию.

Таким образом, при использовании кодов с разделительным знаком для декодирования данной кодовой комбинации требуется знание лишь малой части последовательности, предшествующей декодируемой комбинации.

Одной из основных задач, возникающих при построении систем передачи сообщений, является синхронизация кодирующего и декодирующего устройств или синхронизация кодовых комбинаций. Наличие такой синхронизации позволяет разбить принятую последовательность знаков на кодовые комбинации. В декодирующем устройстве после такой разбивки принятой кодовой комбинации определяется переданный символ. Осуществление и поддержание синхронизации кодовых комбинаций выполняется различно для равномерных и неравномерных кодов.

При использовании равномерных кодов задача осуществления и поддержания синхронизации кодовых комбинаций может решаться следующими способами:

1. с помощью специального синхросигнала, передаваемого в начале сообщения. Момент приема синхросигнала определяет начало первой кодовой комбинации. Начала последующих кодовых комбинаций отсчитываются через интервалы Δt, равные длительности кодовой комбинации.

2. посредством построения кодов без запятой. Эти коды строятся таким образом, что при пропускании через “настроенный” на комбинации данного кода фильтр, последовательности сообщения, закодированного этими кодами, на любом выходе фильтра величина, равная значности используемого кода, будет иметь место только в моменты приема одной из кодовых комбинаций кода.

3. С помощью равномерных кодов с разделительным знаком. Для осуществления синхронизации кодовых комбинаций при использовании данных кодов проще всего использовать фильтр, подобный представленному выше. Фильтр “настраивается” на комбинацию, обозначающую разделительный знак.

При использовании неравномерных кодов синхронизация кодовых комбинаций может осуществляться и поддерживаться различными способами в зависимости от особенностей структуры применяемого кода. Наиболее простой способ рассмотрен нами выше и заключается в использовании неравномерных кодов с разделительным знаком.

Рассмотрев способы построения кодов, обратимся к задаче сокращения избыточности кодовых комбинаций. Одним из способов решения этой задачи является операция статистического кодирования.

Статистическое кодирование имеет целью сократить среднюю длину кодовой комбинации на символ передаваемого сообщения путем учета при кодировании статистических характеристик сообщения.

Очевидно, что сокращения среднего числа знаков кодовых комбинаций можно добиться, если при кодировании символов сообщения некоторым разделимым кодом более короткими кодовыми комбинациями обозначать более вероятные символы. При этом, как было показано, потенциально достижимое сокращение среднего числа знаков при статистическом кодировании определяется энтропией сообщения. Методы статистического кодирования существенно различны при кодировании сообщения, состоящего из статистически независимых символов, и сообщения, состоящего из статистически зависимых символов. В первом случае целесообразно использовать посимвольное кодирование (энтропия H≥ 1), а в случае H > 1 – немнемоническое кодирование. Во втором случае кодированию обычно предшествует декорреляция.

Целесообразность использования методов статистического кодирования при передаче сообщения определяется, прежде всего, величиной достижимого выигрыша в сокращении числа знаков, описывающих сообщение. Для оценки выигрыша необходимо измерять статистические характеристики сообщения. Различные подходы к оценке статистических характеристик сообщений были рассмотрены в предыдущих лекциях, что позволяет нам перейти непосредственно к рассмотрению проблемы минимизации средней длины кодовой комбинации.

Для статистического кодирования могут быть использованы любые разделимые коды. Если ограничиться только кодами, обладающими свойством префикса, то уменьшения потенциально достижимой эффективности кодирования не произойдет. Это объясняется тем, что средняя длина кодовой комбинации однозначно определяется структурной функцией кода. В свою очередь, среди разделимых кодов с заданной структурной функцией всегда имеются коды, обладающие свойством префикса. Использование кодов, обладающих свойством префикса, обеспечивает минимум задержки декодирования и поэтому целесообразно.

Код Шеннона – Фано

Рассмотрим построение кода на примере кодирования русского алфавита. Задача - закодировать двоичным кодом буквы алфавита так, чтобы каждой букве соответствовала определенная комбинация символов 0 и 1, причем среднее число символов на букву текста было минимальным. 31 буква алфавита плюс тире в качестве пробела между словами. Всего 32 символа. Простой подход к решению задачи - приписывание порядковых номеров всем символам по порядку и кодирование присвоенных номеров двоичным кодом: а → 00000, б →00001, в→00010 …, я→11110, “-“ 11111. Этот код не оптимален. Разумнее кодировать часто встречающиеся буквы меньшим числом символов, а редко встречающиеся – большим. Однако, чтобы составить такой код, нужно знать частоты букв в русском тексте, которые можно принять в качестве оценок вероятностей появления букв в тексте. Эти частоты подсчитаны и представлены в порядке убывания (см. таблицу 1).

Таблица 1

Буква	Частота	Буква	Частота	Буква	Частота	Буква	Частота
-	0.145	р	0,041	я	0,019	х	0,009
о	0.05	в	0,039	ы	0.016	ж	0,008
е	0,74	л	0,036	з	0.015	ю	0,007
а	0,064	к	0,029	ъ,ь	0,015	ш	0,006
и	0,064	м	0,026	б	0,015	ц	0,004
т	0,06	д	0,026	г	0,014	щ	0,003
н	0,056	п	0,024	ч	0,013	э	0,003
с	0,047	у	0,021	й	0,010	ф	0,002

Код близок к оптимальному тогда, когда каждый символ передает максимальную информацию. Из свойства 2 энтропии это имеет место в случае равновероятности состояний. Следовательно, в основе оптимального кодирования лежит требование, чтобы в закодированном тексте символы встречались в среднем с одинаковой частотой.

Построение кода, удовлетворяющего поставленному выше условию (кода Шеннона – Фано), производится следующим образом. Кодируемые символы, расположенные в порядке уменьшения частоты, разделяются на две приблизительно равновероятные подгруппы: для первой группы символов на первом месте комбинации ставится 0, а для второй группы символов – 1. Далее каждая группа снова делится на две приблизительно равновероятные подгруппы; для символов первой подгруппы на втором месте ставится 0, а для второй подгруппы -1 и т. д. Построим коды Шеннона – Фано для символов русского алфавита. В соответствии с частотами символов русского алфавита (таблица 1) первое разделение показывает, что в одну группу входят шесть первых символов (сумма частот 0,498), остальные 26 - в другую группу. Следовательно, первые шесть символов на первом месте будут иметь 0, а остальные – 1. На следующем шаге снова разделим символы первой подгруппы на приблизительно равновероятные подгруппы (в первой подгруппе два символа – сумма частот 0, 24, остальные четыре – во второй подгруппе) и опять присвоим 0 символам первой подгруппы и 1 – символам второй. Процесс продолжается до тех пор, пока в каждом подразделении не останется одна буква, которая будет закодирована своим двоичным кодом. Закончив с первой начальной подгруппой, перейдем ко второй начальной подгруппе, которая содержит 26 символов. Коды, полученные в процессе выполнения операций последовательного разделения, приведены в таблице 2.

Таблица 2

Буква	Двоичный код	Буква	Двоичный код	Буква	Двоичный код
-	000	к	10111	ч	111100
о	001	м	11000	й	1111010
е	0100	д	110010	х	1111011
а	0101	п	110011	ж	1111100
и	0110	у	110100	ю	1111101
т	0111	я	110110	ш	11111100
н	1000	ы	110111	ц	11111101
с	1001	з	111000	щ	11111110
р	10100	ъ,ь	111001	э	111111110
в	10101	б	111010	ф	111111111
л	10110	г	111011