1.3 Порядок выполнения работы

1. Написать программу на С++ моделирующую двухслойную нейронную сеть структуры согласно варианту таблицы № 1.

ТАБЛИЦА № 1

№ варианта	Количество входов	Количество скрытых нейронов	Количество выходов	Функция активации в скрытом слое	Функция активации в выходном слое
1	2	5	2	Сигмоидная	Сигмоидная
2	3	7	2	Сигмоидная	Пороговая
3	2	7	1	Сигмоидная	Линейная
4	1	3	2	Сигмоидная	Сигмоидная
5	2	6	1	Сигмоидная	Пороговая
6	3	4	3	Сигмоидная	Линейная
7	2	8	1	Сигмоидная	Пороговая
8	1	9	3	Сигмоидная	Линейная
9	2	4	2	Линейная	Пороговая
10	1	5	1	Пороговая	Линейная
11	1	15	1	Сигмоидная	Сигмоидная
12	2	3	2	Сигмоидная	Пороговая
13	1	56	1	Пороговая	Линейная
14	1	23	2	Линейная	Сигмоидная
15	2	34	1	Пороговая	Сигмоидная
16	1	9	1	Сигмоидная	Пороговая

2. Веса задать случайным образом в диапазоне [-1; 1]. Подать на вход любую последовательность чисел. Построить график зависимости выхода(ов) сети от входа(ов).

3. Увеличить значения весов в 10 раз и повторить пункт 1.3.2

1.4 Контрольные вопросы и понятия

1.4.1 Понятие нейрон. Его математическая модель.

1.4.2 Нейронная сеть.

1.4.3 Свойства сигмоидальной функции активации.

1.4.4 Области применения НС.

1.4.5 Однослойные и многослойные НС.

Лабораторная работа № 2

Изучение нейронных сетей в пакете MatLab на примере аппроксимации тригонометрической функции

1. Цель работы

Знакомство с пакетом MatLab. Получение навыка синтеза нейронных сетей в среде пакета MatLab. Ознакомление с аппроксимирующими свойствами НС.

2. Теоретическая часть

Обучение нейронной сети

Способность к обучению является фундаментальным свойством мозга. В контексте ИНС процесс обучения может рассматриваться как настройка архитектуры сети и весов связей для эффективного выполнения специальной задачи. Обычно нейронная сеть должна настроить веса связей по имеющейся обучающей выборке. Функционирование сети улучшается по мере итеративной настройки весовых коэффициентов. Свойство сети обучаться на примерах делает их более привлекательными по сравнению с системами, которые следуют определенной системе правил функционирования, сформулированной экспертами.

Для конструирования процесса обучения, прежде всего, необходимо иметь модель внешней среды, в которой функционирует нейронная сеть - знать доступную для сети информацию. Эта модель определяет парадигму обучения. Во-вторых, необходимо понять, как модифицировать весовые параметры сети - какие правила обучения управляют процессом настройки. Алгоритм обучения означает процедуру, в которой используются правила обучения для настройки весов.

Существуют три парадигмы обучения: "с учителем", "без учителя" (самообучение) и смешанная. В первом случае нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Веса настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам. Усиленный вариант обучения с учителем предполагает, что известна только критическая оценка правильности выхода нейронной сети, но не сами правильные значения выхода. Обучение без учителя не требует знания правильных ответов на каждый пример обучающей выборки. В этом случае раскрывается внутренняя структура данных или корреляции между образцами в системе данных, что позволяет распределить образцы по категориям. При смешанном обучении часть весов определяется посредством обучения с учителем, в то время как остальная получается с помощью самообучения.

Теория обучения рассматривает три фундаментальных свойства, связанных с обучением по примерам: емкость, сложность образцов и вычислительная сложность. Под емкостью понимается, сколько образцов может запомнить сеть, и какие функции и границы принятия решений могут быть на ней сформированы. Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению. Слишком малое число примеров может вызвать "переобученность" сети, когда она хорошо функционирует на примерах обучающей выборки, но плохо - на тестовых примерах, подчиненных тому же статистическому распределению. Известны 4 основных типа правил обучения: коррекция по ошибке, машина Больцмана, правило Хебба и обучение методом соревнования.

Правило коррекции по ошибке. При обучении с учителем для каждого входного примера задан желаемый выход d. Реальный выход сети y может не совпадать с желаемым. Принцип коррекции по ошибке при обучении состоит в использовании сигнала (d-y) для модификации весов, обеспечивающей постепенное уменьшение ошибки. Обучение имеет место только в случае, когда перцептрон ошибается. Известны различные модификации этого алгоритма обучения.

Обучение Больцмана. Представляет собой стохастическое правило обучения, которое следует из информационных теоретических и термодинамических принципов. Целью обучения Больцмана является такая настройка весовых коэффициентов, при которой состояния видимых нейронов удовлетворяют желаемому распределению вероятностей.

Правило Хебба. Самым старым обучающим правилом является постулат обучения Хебба. Хебб опирался на следующие нейрофизиологические наблюдения: если нейроны с обеих сторон синапса активизируются одновременно и регулярно, то сила синаптической связи возрастает. Важной особенностью этого правила является то, что изменение синаптического веса зависит только от активности нейронов, которые связаны данным синапсом.

Обучение методом соревнования. В отличие от обучения Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, при соревновательном обучении выходные нейроны соревнуются между собой за активизацию. Это явление известно как правило "победитель берет все". Подобное обучение имеет место в биологических нейронных сетях. Обучение посредством соревнования позволяет кластеризовать входные данные: подобные примеры группируются сетью в соответствии с корреляциями и представляются одним элементом.

При обучении модифицируются только веса "победившего" нейрона. Эффект этого правила достигается за счет такого изменения сохраненного в сети образца (вектора весов связей победившего нейрона), при котором он становится чуть ближе ко входному примеру.

Особенности задач оптимизации при обучении многослойной НС

Алгоритм обучения многослойной НС задается набором обучающих правил, которые определяют, каким образом изменяются межнейронные связи в ответ на входное воздействие. На рис. 1 схематично показана процедура обучения многослойной НС.

Вначале определенным образом устанавливаются значения весовых коэффициентов межнейронных связей. Затем из базы данных в соответствии с некоторым правилом поочередно выбираются примеры (пары обучающей выборки X_i, Y_i : входной вектор X_i подается на вход сети, а желаемый результат Y_i на выход сети). По формуле (1) вычисляется ошибка сети Е. Если ошибка велика, то осуществляется подстройка весовых коэффициентов для ее уменьшения, Это и есть процедура обучения сети. В стандартной ситуации описанный процесс повторяется до тех пор, пока ошибка не станет меньше заданной, либо закончится время обучения.

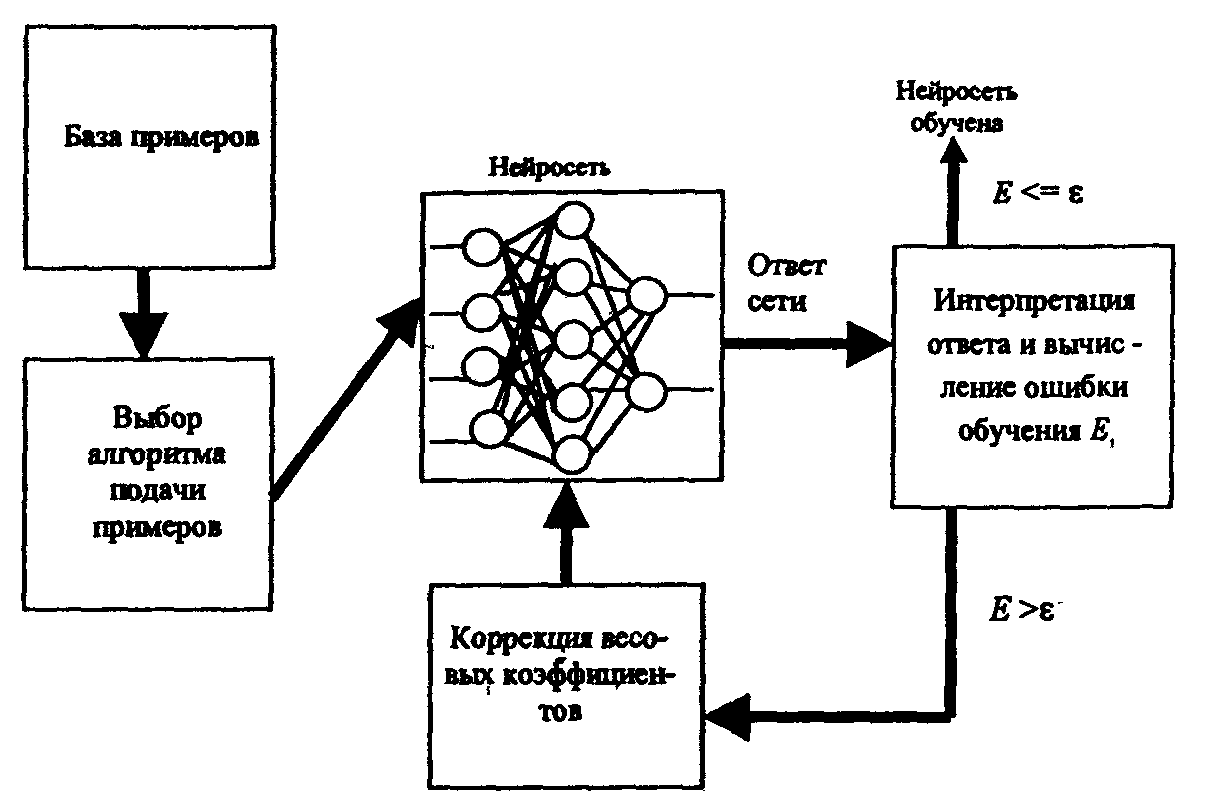
Рис. 1 Процедура обучения многослойной НС

Простейший способ обучения НС - по очереди менять каждый весовой коэф­фициент сети таким образом, чтобы минимизи­ровалась ошибка сети. Этот способ является малоэффективным, целесооб­разнее вычислить совокупность производных ошибки сети по весовым коэффи­циентам - градиент ошибки по весам связей - и изменить все веса сразу на ве­личину, пропорциональную соответствующей производной. Один из возмож­ных методов, позволяющих вычислить градиент ошибки, - алгоритм обратно­го распространения - наиболее известен в процедурах обу­чения НС.

Согласно теореме Геделя о неполноте, никакая система не может быть логически замкнутой: всегда можно найти такую теорему, для доказательства которой потребуется внешнее дополнение. Поэтому критерии выбора модели сложных объектов необходимо разделять на внутренние и внешние.

Внутренние критерии вычисляются на основе результатов эксперимен­тирования с моделью объекта путем подачи на вход сети некоторого входного вектора и фиксации эталонного выходного на ее выходе. При обучении НС на основе примеров (пар) из обучающего множества вычисляется среднеквад­ратичная (или средняя квадратичная ошибка) обучения, которая является внутренним критерием. В этом случае ошибка называется ошибкой обучения.

Для оценки полученной ошибки обучения необходимо использовать внешний критерий, которым является ошибка обобщения Е_обоб, вычисляемая по проверочной (тестовой) выборке. Основная цель обучения НС - создание модели объекта, обладающей свойством непротиворечивости, т.е. такой, в кото­рой ошибка обобщения сохраняется на приемлемом уровне при реализации отображения не только для примеров исходного множества пар (X_i , Y_i), i = 1 ...к, но и для всего множества возможных входных векторов.

Таким образом, если ставится задача синтеза НС для отображения зависимости F: X—> Y с наименьшей ошибкой обучения, то для получения объективного результата проводится разделение исходных данных на две части, называемые обучающей и тестовой выборкой. Критерием правильности окончательных результатов является среднеквадратичная ошибка обобщения, вычисленная по тестовой выборке. Так создается первое внешнее дополнение. Если ставится задача оптимизации разделения данных на обучающую и проверочную части, то требуется еще одно внешнее дополнение. База данных в этом случае разбивается на три части: обучающую, тестовую, подтверж­дающую выборки. В этом случае на подтверждающей выборке проверяется адекватность получаемого отображения F: X->Y объекту с задаваемой ошиб­кой обобщения. При конструировании такого отображения задача обучения НС является многокритериальной задачей оптимизации, поскольку необходимо найти общую точку минимума большого числа функций. Для обучения НС необходимо принятие гипотезы о существовании общего минимума, т.е. такой точки в поисковом пространстве, в которой значение всех оценочных функ­ций по каждой связи вход-выход близки к экстремуму. Опыт, накопленный при решении практических задач на НС показывает, что такие точки существуют.

Многокритериальность и сложность зависимости функции оценки Е от параметров НС, приводит к тому, что адаптивный рельеф (график функции оценки) может содержать много локальных минимумов. Таким образом, при поиске минимальной ошибки Е желательно использовать стохастические и глобальные методы оптимизации, такие как имитация отжига и генетический алгоритм.

Кроме того, к методам оптимизации, использующимся в процедуре обуче­ния НС, добавляют еще следующие требования. Во время процедуры обуче­ния необходимо, чтобы НС могла обретать новые навыки без потери старых, т.е. ошибка обобщения должна оставаться на приемлемом уровне. Это означает, что в достаточно большой окрестности существования точки общего мини­мума значения функции оценки Е_о6о6 не должны существенно отличаться от минимума. Иными словами, точка общего минимума должна лежать в доста­точно широкой области изменения функций оценки.

Свойства алгоритма обратного распространения ошибки (Back Propagation - ВР)

ВР – это итеративный градиентный алгоритм обучения многослойной НС без обратных связей. В такой сети на каждый нейрон первого слоя подаются все компоненты входного вектора. Все выходы скрытого слоя m подаются на слой m+1 и т.д., т.е. сеть является полносвязной. При обучении ставится задача минимизации ошибки НС, которая определяется методом наименьших квадра­тов:

_p

E(W) = ½ ∑ (y_j – d_j)² , (1)

^j=1

где у_j - значение j-гo выхода НС;

d_j - желаемое значение j-ro выхода; р - число нейронов в выходном слое.

Некоторые трудности, связанные с применением данного алгоритма в процедуре обучения НС:

Медленная сходимость процесса обучения. Сходимость ВР строго дока­зана для дифференциальных уравнений, т.е. для бесконечно малых шагов в пространстве весов. Но бесконечно малые шаги означают бесконечно большое время обучения. Следовательно, при конечных шагах сходимость алгоритма обучения не гарантируется.

Переобучение. Высокая точность, получаемая на обучающей выборке, может привести к неустойчивости результатов на тестовой выборке. Чем лучше сеть адаптирована к конкретным условиям (к обучающей выборке), тем мень­ше она способна к обобщению и экстраполяции. В этом случае сеть моделиру­ет не функцию, а шум, присутствующий в обучающей выборке. Это явление называется переобучением. Кардинальное средство борьбы с этим недостатком - использование подт­верждающей выборки примеров, которая используется для выявления пере­обучения сети. Ухудшение характеристик НС при работе с подтверждающей выборкой указывает на возможное переобучение. Напротив, если ошибка последовательно уменьшается при подаче примеров из подтверждающегося множества, сеть продолжает обучаться. Недостатком этого приема является уменьшение числа примеров, которое можно использовать в обучающем множестве (уменьшение размера обучающей выборки снижает качество работы сети). Кроме того, возникает проблема оптимального разбиения исходных дан­ных на обучающую, тестовую и подтверждающую выборку. Даже при слу­чайной выборке разные разбиения базы данных дают различные оценки.

«Ловушки», создаваемые локальными минимумами. Детерминирован­ный алгоритм обучения типа ВР не всегда может обнаружить глобальный минимум или выйти из него. Одним из способов, позволяющих обходить «ло­вушки», является расширение размерности пространства весов за счет увели­чения скрытых слоев и числа нейронов скрытого слоя. Другой способ - ис­пользование эвристических алгоритмов оптимизации, один из которых - ге­нетический алгоритм.

Эвристический алгоритм оптимизации на основе генетического поиска

Суть генетического алгоритма. Рассмотрим возможность использования в процедуре обучения многослойной НС одного из методов эвристической оп­тимизации - генетического алгоритма (ГА), моделирующего процессы при­родной эволюции и относящегося к так называемым эволюционным методам поиска.

При практической реализации данных алгоритмов на каждом шаге исполь­зуются стандартные операции, изменяющие решение. С помощью ГА можно получить решение, соответствующее глобальному оптимуму или близкое к нему, при этом на каждом шаге проводятся некоторые стандартные операции одновременно над множеством решений (популяций), что позволяет значи­тельно увеличить скорость приближения к экстремуму.

Основные отличия ГА от стандартных локальных (например, градиентных) и глобальных (например, случайных) алгоритмов оптимизации:

• поиск субоптимального решения основан на оптимизации случайно задан­ного не одного, а множества решений, что позволяет одновременно анализи­ровать несколько путей приближения к экстремуму; при этом оценка получае­мых результатов на каждом шаге позволяет учитывать предыдущую информацию, т.е. происходит эволюционное развитие оптимальных решений;

• решения рассматриваются как некоторые закодированные структуры (символьные модели), а не как совокупность параметров, что позволяет в не­которых случаях значительно уменьшить время преобразования данных, т.е. увеличить скорость приближения к экстремуму;

• для оценки «пригодности» решения и последующего эволюционного развития наряду с использованием целевой функции дополнительно моделируются «правила выживания», которые расширяют разнообразие множества реше­ний и определяют эволюционное развитие;

• при инициализации, преобразовании и других видах операций с решения­ми используются вероятностные, а не детерминированные правила, которые вносят в направленность генетического поиска элементы случайности; тем самым решается проблема выхода из локальных оптимумов;

• отсутствует необходимость расчета производных от целевой функции (как в градиентных ме­тодах) или матрицы производных второго порядка (как в квазинью­тоновских).

Схема простого генетического алгоритма представлена на рис. 2.

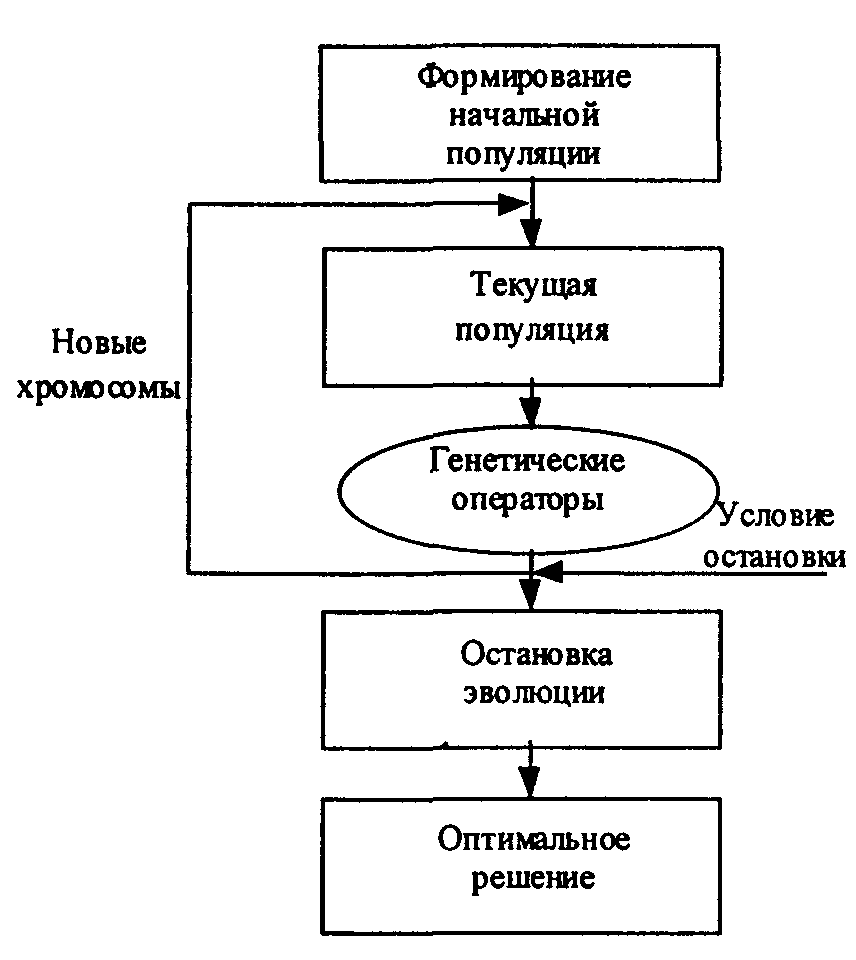
Рис. 2 Схема простого генетического алгоритма

Генетическим алгоритмом называется следующий объект:

ГА( Р°, r, l, sl, Fit, cr, m, ot),

где ГА - генетический алгоритм; Р° - исходная популяция; r - ко­личество элементов популяции; l - длина битовой строки, коди­рующей решение: sl – оператор селекции; Fit - функция фитнесса (функция полезности), определяющая «пригодность» решения; сr - оператор кроссинговера, определяющий возможность получения нового решения; т - оператор мутации; ot - оператор отбора.

Наименьшей неделимой единицей биологического вида, подверженной действию факторов эволюции, является особь Н^t_к (к - номер особи, t — момент времени эволюционного процесса). В качестве аналога особи в задаче опти­мизации принимается произвольное допустимое решение X Є D, которому присвоено имя Н^t_к. Действительно, вектор X - это наименьшая неделимая единица, характеризующая в экстремальной задаче внутренние параметры объекта оптимизации на каждом t-м шаге поиска оптимального решения, которые изменяют свои значения в процессе минимизации некоторого крите­рия оптимальности J(X).

Формирование популяции. Совокупность особей (Н^t₁, ..., Н^t_r) образуют популяцию Р^t (численностью r). Эволюция популяции Р^t рассматривается как чередование поколений (рис. 3). Номер поколения отождествляется с момен­том времени t = 0,1,..,Т, где T - жизненный цикл популяции, определяющий период ее эволюции. Совокупность генотипов всех особей Н^t_к образует хромо­сомный набор, который полностью содержит в себе генетическую информацию.

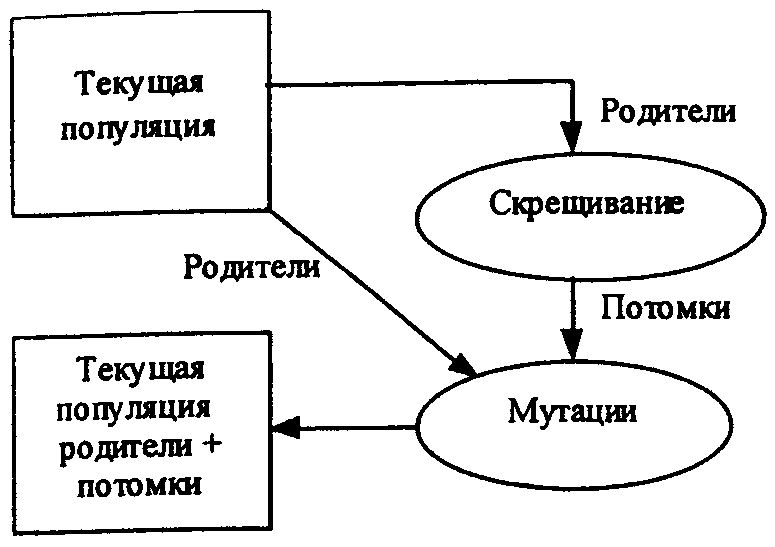
Рис. 3 Формирование популяции

Способы создания начальной популяции Р°. В настоящее время наиболее известными являются три стратегии создания начального мно­жества решений:

1) формирование полной популяции;

2) генерация случайного множества решений, достаточно большого, но не исчерпывающего все возможные вари­анты;

3) генерация множества решений, включающего разновидности одного решения.

При первой стратегии должен быть реализован полный набор всевозможных решений, но это невозможно из-за чрезмерных вычислительных затрат и боль­шой области поиска для задач высокой размерности. Стартовая популяция, соз­данная на основе данной стратегии, не может развиваться, т.е. в ней уже содер­жатся все решения, в том числе и оптимальные.

Третью стратегию применяют, когда есть предположение, что некоторое ре­шение является разновидностью известного. В этом случае происходит выход сразу в область существования экстремума, и время поиска оптимума зна­чительно сокращается.

Для большинства задач проектирования первая (вследствие пробле­матичности полного перебора) и третья (из-за сужения области поиска и боль­шой вероятности попадания в локальный экстремум) стратегии неприемлемы. Наиболее перспективной является вторая стратегия, так как она в результате эволюции популяции создает возможность перехода из одной подобласти области поиска в другую и имеет сравнительно небольшую размерность задачи оптимизации.

Эффективность ГА, качество получаемого решения и успех дальнейшего развития эволюции во многом определяются структурой и качеством начальной популяции. Наиболее целесообразным представляется подход, основанный на комбинировании второй и третьей стратегии: путем предварительного анализа решаемой задачи выявляются подобласти в области поиска, в кото­рых могут находиться оптимальные решения, т.е. определяются особи с высоким значением фитнесса, а затем случайным образом формируются стартовые решения в этих подобластях.

Примеры генетических операторов

Выделяют два основных способа генерации новых решений:

1. путем перекомпоновки (скрещивания) двух родительских решений (оператор скрещивания или кроссинговер сr) (рис. 4);

2. путем случайной перестройки отдельных решений (оператор мутации т) (рис. 5).

Рис. 4 Одноточечный кроссинговер Рис. 5 Оператор мутации

Кроссинговер сr производит структурированный и рандомизированный обмен информацией внутри родительской пары, т.е. между двумя хромосома­ми, формируя новые решения. Задача создания потомков состоит в выборе такой комбинации участков хромосом, которая давала бы наилучшее решение. Таким образом, основная цель скрещивания заключается в накоплении всех лучших функциональных признаков, характеризующих отдельные участки хромосом, копируемых в конечном решении.

Применение оператора мутации т в процессе биологической эволюции предотвращает потерю важного генетического материала; в генетических алгоритмах т используется для выхода из локальных экстремумов. На практике при использовании ГА для решения задач оптимизации встречаются классические операторы генной мутации: изменение величины случайно выбранного гена (рис. 5). Для улучшения технологии генетического поиска оптимальных решений целесообразно применять операторы хромосомной мутации.

Значительное улучшение качества и скорости сходимости ГА дает комби­нирование ГА с классическими детерминированными методами оптимизации, разработка модифицированных операторов кроссинговера и мутации, основан­ных на знании решаемой задачи.

Селекция решений

Качество поколений потомков во многом зависит от выбора операторов се­лекции si родительской пары. Поэтому для аккумуляции всех лучших функ­циональных признаков, имеющихся в популяции, используют подбор хромо­сом для скрещивания. Наиболее часто в ГА применяют следующие типы опе­раторов si:

1. случайный выбор пар;

2. предпочтительный выбор на основе функции фитнесса.

Алгоритм имитации отжига

Метод имитации отжига основан на идее, заимствованной из статической механики. Он отражает поведение материального тела при отвердевании с применением процедуры отжига при температуре, последовательно понижаемой до нуля. При отвердевании расплавленного материала его температура должна уменьшаться постепенно, вплоть до момента полной кристаллизации. Если процесс остывания протекает слишком быстро, образуются значительные нерегулярности структуры материала, которые вызывают внутренние напряжения. В результате общее энергетическое состояние тела, зависящее от его внутренней напряженности, остается на гораздо более высоком уровне, чем при медленном охлаждении. Быстрая фиксация энергетического состояния тела на уровне выше нормального аналогична сходимости оптимизационного алгоритма к точке локального минимума. Энергия состояния тела соответствует целевой функции, а абсолютный минимум этой энергии - глобальному минимуму. В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация тела сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на какое-то время возрастать (в частности, при подогреве тела для предотвращения слишком быстрого его остывания. Благодаря допустимости кратковременного повышения энергетического уровня возможен выход из ловушек локальных минимумов, которые возникают при реализации процесса. Только понижение температуры тела до абсолютного нуля делает невозможным какое-либо самостоятельное повышение его энергетического уровня. В этом случае любые внутренние изменения ведут только к уменьшению общей энергии тела.

В реальных процессах кристаллизации твердых тел температура пони­жается ступенчатым образом. На каждом уровне она какое-то время поддерживается постоянной, что необходимо для обеспечения терми­ческого равновесия. На протяжении всего периода, когда температура оста­ется выше абсолютного нуля, она может как понижаться, так и повышаться. За счет удержания температуры процесса поблизости от значения, соответствующего непрерывно снижающемуся уровню термического равновесия, удается обходить ловушки локальных минимумов, что при достижении нулевой температуры позволяет получить и минимальный энергетический уровень.

Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Предложенный Н. Метрополисом в 1953г. и доработанный многочисленными после­дователями, он в настоящее время считается одним из немногих алгоритмов, позволяющих практически находить глобальный минимум функции нескольких переменных.

Классический алгоритм имитации отжига можно описать следующим образом.

1. Запустить процесс из начальной точки w при заданной начальной температуре Т = Т_mах.

2. Пока T > 0, повторить L раз следующие действия:

• выбрать новое решение w' из окрестности w;

• рассчитать изменение целевой функции Δ = E(w') - E(w);

• если Δ <= 0, принять w = w'; в противном случае (при Δ > 0) принять, что w = w' с вероятностью ехр(-Δ /Т) путем генерации случайного числа R из интервала (0,1) с последующим сравнением его со зна­чением ехр(-Δ /Т); если ехр(-Δ /Т) > R, принять новое решение w = w'; в противном случае проигнорировать его.

3. Уменьшить температуру (Т < rТ) с использованием коэффициента уменьшения r, выбираемого из интервала (0,1), и вернуться к п. 2.

4. После снижения температуры до нулевого значения провести обучение сети любым из представленных выше детерминированных методов, вплоть до достижения минимума целевой функции.

В описании алгоритма в качестве названия параметра, влияющего на вероятность увеличения значения целевой функции, используется выбран­ный его автором Н. Метрополисом термин "температура", хотя с формальной точки зрения приведенная модель оптимизации является только математической аналогией процесса отжига. Алгоритм имитации отжига выглядит кон­цептуально несложным и логически обоснованным. В действительности приходится решать много фундаментальных проблем, которые влияют на его практическую применимость. Первой следует назвать проблему длительности имитации. Для повышения вероятности достижения глобального минимума длительность отжига (представляемая количеством циклов L, повторяемых при одном и том же значении температуры) должна быть достаточно большой, а коэффициент уменьшения температуры r - низким. Это увели­чивает продолжительность процесса моделирования, что может дискреди­тировать его с позиций практической целесообразности.

Возникает проблема конкурентоспособности метода по сравнению, например, с методами локальной оптимизации в связи с возможностью многократного возобновления процесса из различных точек в пространстве параметров. При таком подходе грамотная статистическая обработка позволяет с высокой вероятностью и достаточно быстро локализовать зону глобального минимума и достичь его с применением технологии детерминированной оптимизации.

Большое влияние на эффективность метода имитации отжига оказывает выбор таких параметров, как начальная температура T_mах, коэффициент уменьшения температуры r и количество циклов L, выполняемых на каждом температурном уровне.

Максимальная температура подбирается по результатам многочисленных предварительных имитационных экспериментов. На их основе строится распределение вероятности стохастических изменений текущего решения при конкретных значениях температуры (зависимость А = f/(T)). В последующем, задаваясь процентным значением допустимости изменений в качестве порогового уровня, из сформированного распределения можно найти искомую начальную температуру. Главной проблемой остается определение порогового уровня, оптимального для каждой реализации процесса имитации отжига. Для отдельных практических задач этот уровень может иметь различные значения, однако общий диапазон остается неизменным. Как правило, начальная температура подбирается так, чтобы обеспечить реализацию порядка 50% последующих случайных изменений решения. Поэтому знание предварительного распределения вероятностей таких изменений позволяет получить приблизительную оценку начальной температуры.

Методики выбора как максимального количества циклов L для кон­кретных температурных уровней, так и определение значения коэффи­циента уменьшения температуры r не столь однозначны. При подборе этих параметров приходится учитывать динамику изменения величины целевой функции в зависимости от количества выполненных циклов обучения.

Большая часть вычислительных ресурсов расходуется на начальной стадии процесса, когда средняя скорость изменения целевой функции неве­лика и прогресс оптимизации минимален. Это "высокотемпературная" стадия имитационного процесса. Быстрее всего величина целевой функции уменьшается на средней стадии процесса при относительно небольшом количестве приходящихся на нее итераций. Завершающая стадия процесса имеет стабилизационный характер. На ней независимо от количества итераций прогресс оптимизации становится практически незаметным. Такое наблюдение позволяет существенно редуцировать начальную стадию отжига без снижения качества конечного результата. Модификации обычно подвергается количество циклов, выполняемых при высоких температурах, оно сокращается в случае, когда оказался выполненным весь запланированный объем изменений текущего решения. Такой подход позволяет сэкономить до 20% времени.

Исключение последней, плоской части характеристической кривой целевой функции также возможно. В соответствии с обычным критерием остановки алгоритма, если при нескольких последовательных снижениях температуры не регистрируется уменьшение величины целевой функции, то процесс останавливается, а наилучшее достигнутое решение считается глобальным минимумом. Дальнейшее уменьшение критерия остановки не рекомендуется, поскольку оно ведет к снижению вероятности достижения глобального минимума. В то же время заметное влияние на конечную стадию процесса оказывают коэффициент понижения температуры r и количество циклов L. Ее длительность удается сократить более частым изменением температуры при уменьшении количества циклов, но при сохранении неизменным общего объема итераций.

Еще одна проблема связана с определением длительности моделирования процесса отжига, пропорциональной суммарному количеству итераций. Поскольку отводимое для оптимизации время всегда ограничено, все его можно потратить либо на одну реализацию процесса с соответствующим удлинением циклов, либо сократить длительность всех циклов, а за счет этого выполнить несколько реализаций и принять в качестве результата наилучшее решение. В ходе различных компьютерных экспериментов установлено, что при малом лимите времени лучшие результаты дает единичная реализация. Если же моделирование может быть более длительным, статистически лучшие результаты достигаются при многократной реализации процесса имитации отжига, при больших (близких к 1) значениях коэффициента r.

Наибольшее ускорение процесса имитации отжига можно достичь путем замены случайных начальных значений весов w тщательно подобранными значениями с использованием любых доступных способов предварительной обработки исходных данных. В такой ситуации в зависимости от количества оптимизируемых весов и степени оптимальности начальных значений удается добиться даже многократного сокращения времени моделирования.