26-04-2013_18-59-09 / Прогнозные модели

Прогнозные модели

Величина d=2,44 совпадает с размерностью модели сборки фрактального кластера по типу присоединения частица - кластер, при условии случайного блуждания частиц.

Выразим подмножества перколяционного кластера в порядке их возрастания по формуле:

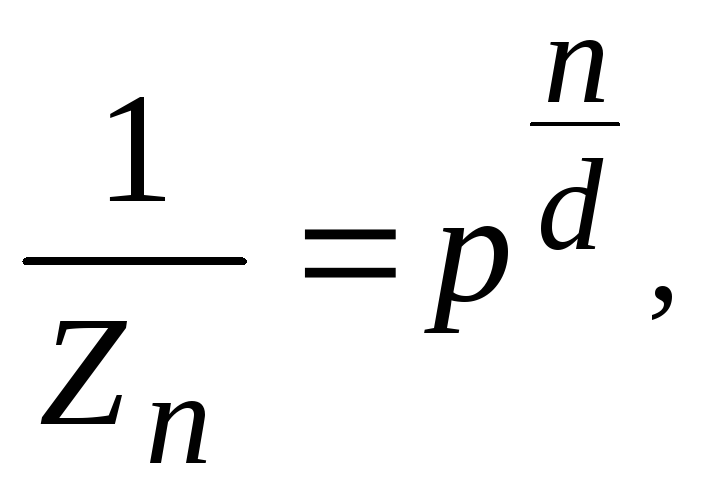
где n - порядок подмножества в виде равенств:

.

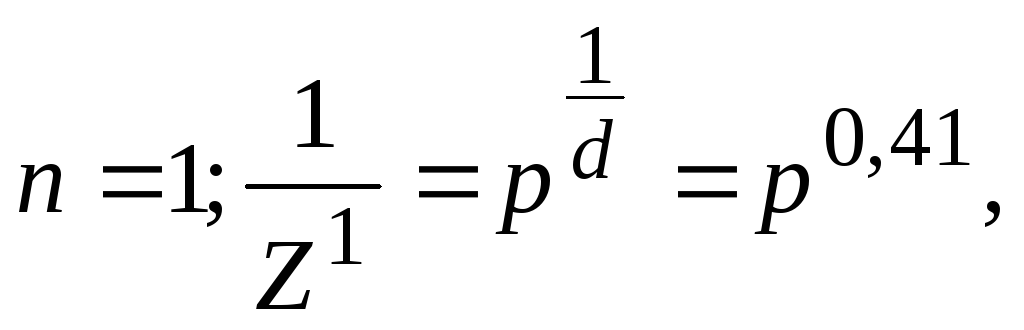
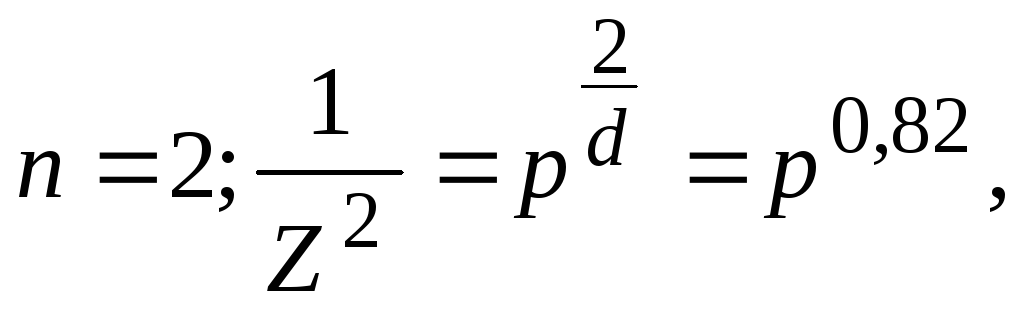
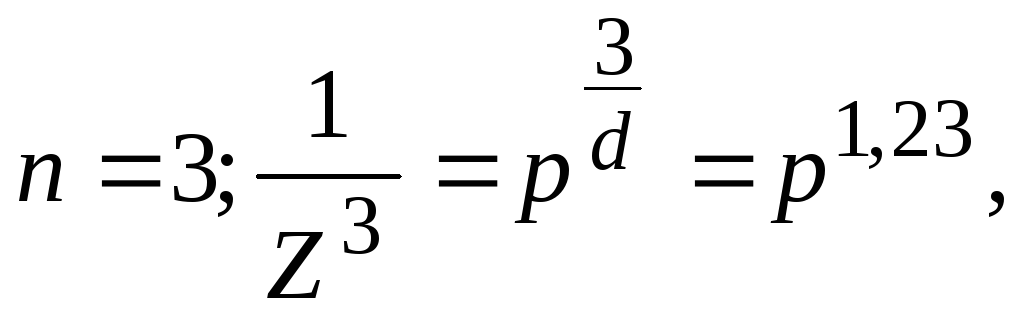
Из полученных соотношений видно, что численные величины показателя степени параметра p для данных подмножеств весьма точно укладываются в допустимый интервал значений критических индексов, которые даются моделью перколяции для трехмерных систем и достаточно подробно обсуждаются различными авторами.

В качестве элементарной составляющей глобальной структуры композита принимаем цепочку из частиц наполнителя, связанных пленочной матрицей.

Формализуем строение цепочки условной ли­нией. В качестве элементарной ячейки структуры полимерного композита прини­маем, трехчастичную ячейку, как минимально возможную. Форма­лизуем строение ячейки плоской фигурой. Подобным образом можно продолжить наращивание масштаба до формирования структурного каркаса. При этом получается плоская модель фрактальной струк­туры композита с самоподобным отражением (рис. 2.9).

С учетом произведенного моделирования можно выделить четыре основных струк­турных элемента, которыми являются — цепочка из частиц наполнителя, связан­ных между собой упрочненными плёночными прослойками полимер­ной матрицы; ячейка, образованная цепочечными элементами; струк­турный каркас, сформированный из цепочечных и ячеистых эле­ментов; струк­турный каркас, сформированный в основном из ячеистых эле­ментов. Каждый из четырех элементов характеризуется определённым универсальным критическим индексом.

Индекс b₃ характеризует цепочное строение перколяционного кластера (рис. 2.9, а).

Индекс n₃ отвечает за ячеистое строение перколяционного кластера (рис. 2.9, б).

Индекс t₃ в фрактальном рассмотрении определяет крупноячеистый остов фрактального перколяционного каркаса (рис. 2.9, г).

Индекс g₃ отвечает за тупиковые ветви структурного каркаса перколяционного кластера (рис. 2.9, в).

В этой связи при изучении физико-механических показателей композита необходимо предвари­тельно определить, какой из четырех основных структурных элементов отвечает за изменение контролируемого показателя.

В результате проведенного анализа установлено, что перколяционный кластер, состоящий из неупорядоченно-распределенных в матрице дисперсных частиц наполнителя, имеет фрактальную структуру с размерностью d = 2,44.

b₃ n₃

а) б)

g₃ t₃

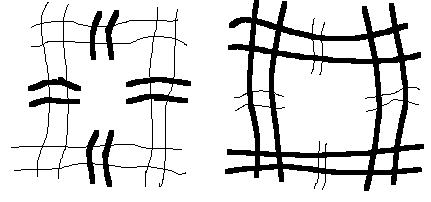
в) г)

Рис. 2.9. Топологическая модель структуры демпфирующих

композитов

Критические индексы связаны с фрактальной размерностью зависимостями:

Критические индексы имеют важное значение при анализе демп-фирующих физико-механических свойств наполненных полимерных композитов, так как они выступают в роли интегральных универсальных показателей состояний этих специфических систем и могут эффективно использоваться при прогнозировании вновь разрабатываемых вибропоглощающих материалов.

В работах [4, 6] установлено, что за изменение упругих свойств отвечает жесткий структурный каркас. Действительно, упругие деформации способен передавать лишь жесткий структурный каркас, пронизывающий весь объём композита. В свою очередь свободно свисающие структур­ные цепочки не способны передавать деформацию упругости.

Таким образом, за изменение модуля упругости полимерного композита отвечает индекс t. Отсюда следует, что чем содержание наполнителя в композите больше, тем более плотный структурный каркас формируется в его объеме.

Прочность композита, в отличие от упругих свойств полимерного материала зависит от общего количества цепочек, пересекающих предполагаемую поверхность разрушения. Для данного случая должны рассматриваться все це­почки, пересекающие поверхность разрушения, как входящие в сос­тав жесткого структурного каркаса, так и свободно свисающие. Поэтому изменение прочности в процессе наполнения композита зависит от индекса v.

В предложенном представлении массопоглощение и демпфирование композитов в области высокого наполнения зависит от размера ячеистой структуры (индекс  и ), а в области низкого только от .

Одним из основных показателей вибродемпфирующих свойств дисперсно-наполненных композитов является коэффициент внутреннего трения (Q^-1).

Применение дисперсных наполнителей из пористых материалов, плохо смачивающихся матричным связующим, приводит к эффективному повышению коэффициента внутреннего трения наполненных полимерных композитов. Такие зависимости практически не анализировались ранее, поэто­му четких функциональных интерпретаций, описывающих их не существует.

Уравнение, полученное с помощью методов теории перколяции (протекания) и описывающее поведение коэффициента внутреннего трения в зависимости от u пористого наполнителя, имеет вид:

Q_c^-1 = Q_m^-1(1+au^ ) (2.8)

где Q_m^-1- коэффициент внутреннего трения матричного модифицированного материала; 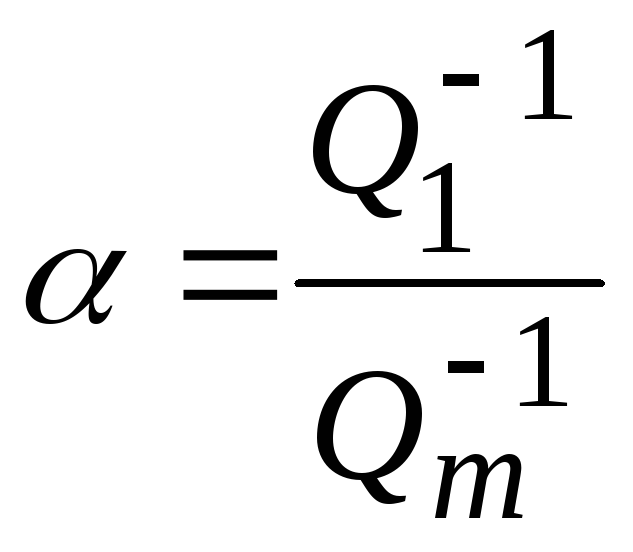- коэффициент внутреннего трения единичного эле­мента; g - критический индекс.

Необходимо отметить, что использование этого уравнения справедливо лишь в том случае, когда в качестве дисперсного наполнителя используется пористый материал с относительно невысокими упругими показателями.

Рассмотрим структуру полимерного дисперсно-наполненного композита с позиции модели Шкловского – де Жена. Модель предполагает формирование суперструктуры бесконечного перколяционного кластера в виде искаженного пространственного каркаса, пронизывающего матричный объем (полимер в состоянии массива) и образованного из цепочек частиц наполнителя, связанных между собой прослойками полимерной матрицы (полимер в состоянии пленочных адсорбционных слоев). На рис.2.10 изображен фрагмент бесконечного перколяционного кластера.

Считается, что точка принадлежит скелету бесконечного кластера, если по крайней мере два пути, выходящие из нее в разные стороны позволяют уйти на бесконечное расстояние. Такой точкой, например, является точка C. Если только один путь, выходящий из точки ведет в бесконечность, то эта точка принадлежит тупиковым ветвям (точка D или E). Поэтому считается, что точки D и E лежат на тупиковых ветвях бесконечного кластера. В качестве элементарной составляющей глобальной структуры полимерного композита принимаем цепочку из частиц наполнителя, связанных пленочной матрицей. Формализуем строение цепочки условной линией. В качестве элементарной ячейки структуры полимерного композита принимаем трехчастичную ячейку, как минимально возможную. Формализуем строение ячейки плоской фигурой. Подобным образом можно продолжить наращивание масштаба до формирования структурного каркаса. При этом получается плоская модель фрактальной структуры композита с самоподобным отображением (рис.2.9).

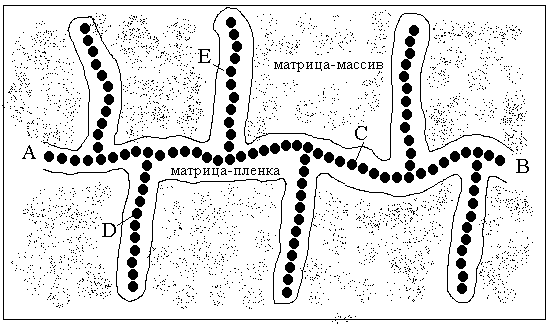
Рис. 2.10. Фрагмент бесконечного перколяционного кластера

вибродемпфирующего композита

Рассчитанный критический индекс g =1,23 в результате усреднения по всем использованным данным экспериментов [65] находится в интервале допустимых значений критического индекса, являющегося универсальным для трехмерных систем, и отвечающего за тупиковые ветви бесконечного кластера. Наличие тупиковых ветвей в структуре полимерного композита подтверждается экспериментальными исследованиями, представленными на рис.2.11. Из сказанного следует, что именно мертвые концы определяют рост коэффициента внутреннего трения наполненной композитной системы.

Полученный критический индекс свидетельствует о том, что основной механизм диссипации колебательной энергии сосредоточен в тупиковых ветвях бесконечного кластера.

При описании упругих свойств композитов c усиливающим наполнителем в зависимости от  используется множество уравнений [6]. К наиболее распространенным уравнениям следует отнести:

- уравнение верхнего предела модуля упругости (случай равных деформаций)

E_c = E_m (1 - ) + E_f ,

где E_m - модуль упругости матричного материала, E_f - модуль упругости материала наполнителя;

- уравнение нижнего предела модуля упругости (случай равных напряжений)

; (4.2)

- уравнение Эйнштейна

E_c = E_m( 1 + 2,5);

- уравнение Гута-Смолвуда

E_c = E_m(1 + 2,5 + 14,1²);

- уравнение Эйлерса-Ван-Дийка

;

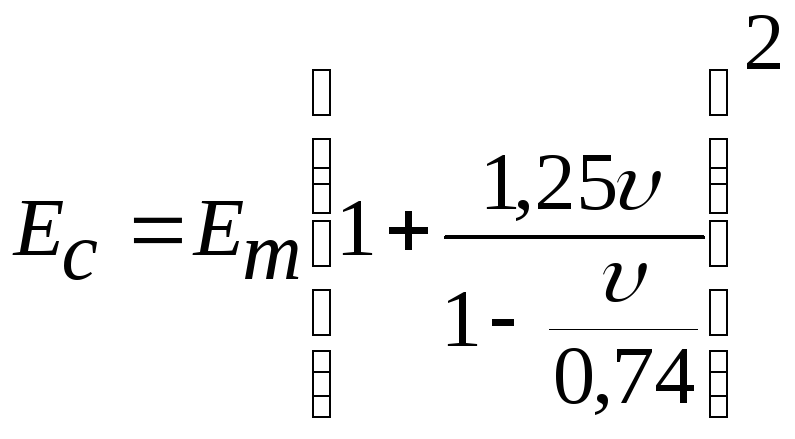• уравнение Кернера

,

где ;

 - коэффициент Пуассона (для полимеров 0,5);

- уравнение Муни

;

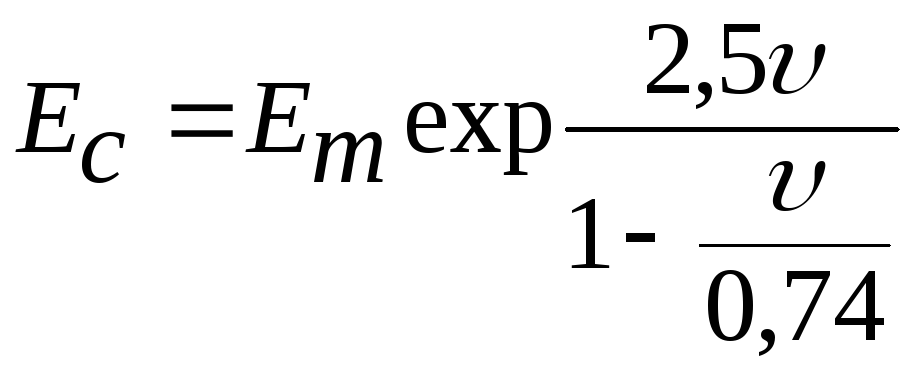- уравнение Сяо-Халпина

,

где ;

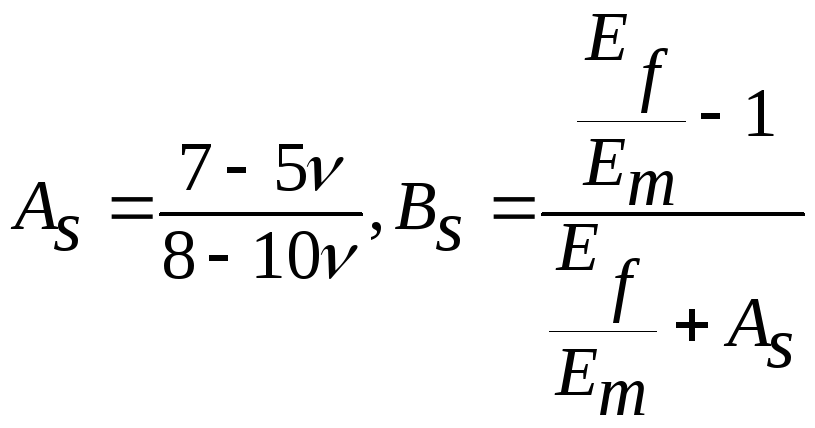- уравнение Нильсена

,

где ,  = 0,74 - плотность правильной плотнейшей упаковки монодисперсных сферических частиц;

- уравнение Исаи

,

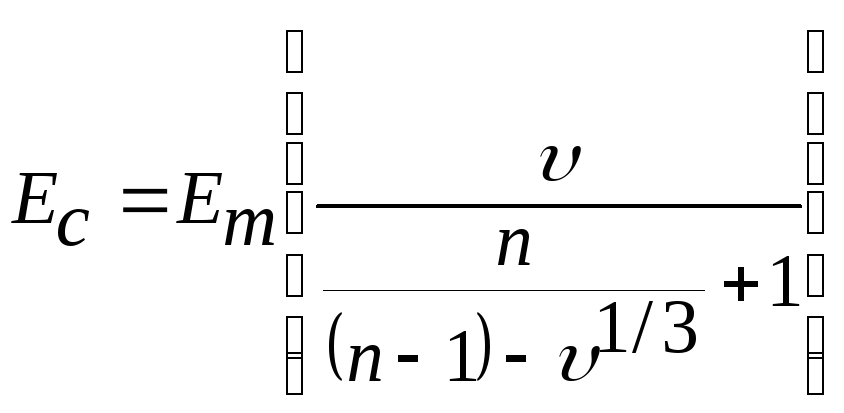где ;

- уравнение, полученное с помощью методов теории протекания

, (4.3)

где - модуль упругости единичного цепочечного элемента перколяционного фрактального каркаса структуры композита.

В области высокого наполнения решение уравнений существенно отличаются между собой. Наиболее близкое решение, включая и область высокого наполнения к экспериментальным значениям Е_д, дает уравнение (4.3), которое может эффективно использоваться в предварительной оценке упругих свойств вновь разрабатываемых композитов.

Прочность термореактивного композита зависит от общего количества цепочек, пересекающих поверхность разрушения. В результате проведения экспериментально-теоретических исследований установлено, что предел прочности при одноосном сжатии эффективно описывается перколяционной зависимостью: R_сж.с= R_сж.с(1+α_сж^ν), где R_сж.с и R_сж.m - предел прочности при одноосном сжатии КМ и матричного материала; - предел прочности при одноосном сжатии единичного элемента КМ.

был проведён сравнительный анализ данных экспериментов по K_з для эпоксидных, полиэфирных и эпоксиполиуретановых композитов и расчётных значений, полученных с помощью методов теории протекания (рисунки 3.20-3.22, приложение 2). С учётом всех использованных опытных величин и получено уравнение в виде:

К_з=К_з.м. (1+). (4.2)

где K_з.м. - коэффициент поглощения звука полимерной матрицы; - коэффициент поглощения звука единичного структурного элемента композита; - критический индекс.

Рассчитанный критический индекс =1,23 лежит в пределах допустимых значений классического критического индекса и свидетельствует о том, что именно в тупиковых ветвях структурного каркаса сосредоточен основной механизм звукопоглощения КМ.

8