
- •10.7 . 10.8.
- •10.9. 10.10.
- •10.11. 10.12. 10.13. 10.14.
- •10.15. 10.16.
- •10.17 ,,,.
- •10.27 .
- •10.74 ,,. 10.75,,.
- •10.76 ,. 10.77,.
- •§3. Тройной интеграл.
- •10.81 . 10.82.
- •10.83 . 10.84.
- •10.85 . 10.86.
- •10.87. 10.88.
- •10.89 ,.,,,.
- •10.95 .
- •10.113 ,,,.
- •10.131 ,.
- •10.132 ,,.
- •10.133 ,,,.
- •10.134 ,,.
- •§5. Несобственные кратные интегралы.
- •10.143 . 10.144.
10.7 . 10.8.
Имеет место
равенство
 =
=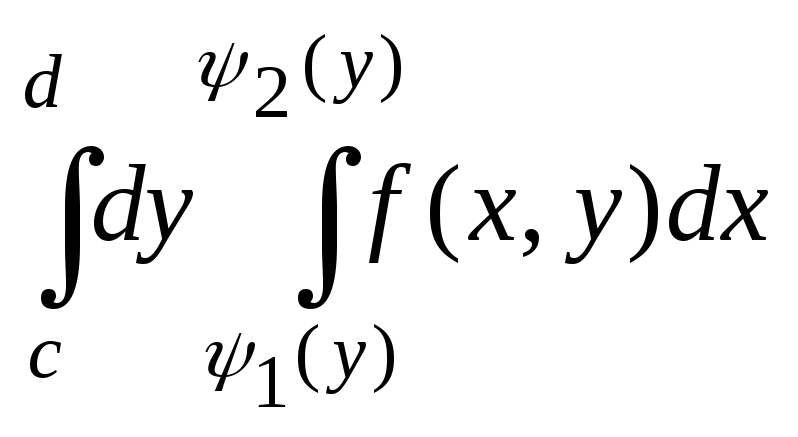 ,
если
,
если![]() .
Если
.
Если![]() не является множеством такого вида, то
при изменении порядка интегрирования,
её представляют в виде конечного
объединения непересекающихся (без общих
внутренних точек) областей
не является множеством такого вида, то
при изменении порядка интегрирования,
её представляют в виде конечного
объединения непересекающихся (без общих
внутренних точек) областей![]() ,
каждая из которых является элементарной
в направлении той или другой координатной
оси. Тогда в силу аддитивности повторный
интеграл по области
,
каждая из которых является элементарной
в направлении той или другой координатной
оси. Тогда в силу аддитивности повторный
интеграл по области![]() будет равен сумме повторных интегралов
по областям
будет равен сумме повторных интегралов
по областям![]() .
.
Представление
области
![]() в виде
в виде![]() ,
часто существенно упрощается при
изображении области
,
часто существенно упрощается при
изображении области![]() на чертеже.
на чертеже.
В задачах 10.9-10.16 изменить порядок интегрирования в следующих повторных интегралах:
10.9. 10.10.
10.11. 10.12. 10.13. 10.14.
10.15. 10.16.
Двойным
интегралом
от непрерывной функции
![]() по ограниченной замкнутой области
по ограниченной замкнутой области![]() называется число
называется число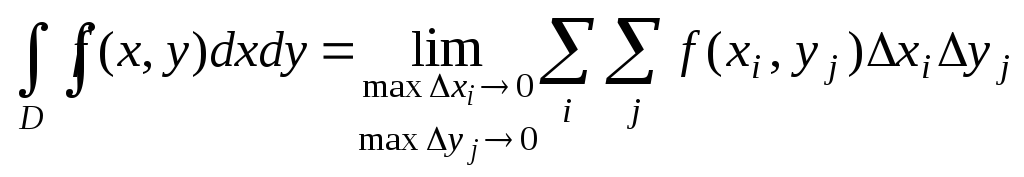 ,
где
,
где![]() ,
,![]() и суммирование ведётся по тем значениям
и суммирование ведётся по тем значениям![]() и
и![]() ,
для которых
,
для которых![]() .
.
Двойной интеграл
по области
![]() вычисляется по формуле
вычисляется по формуле
![]()
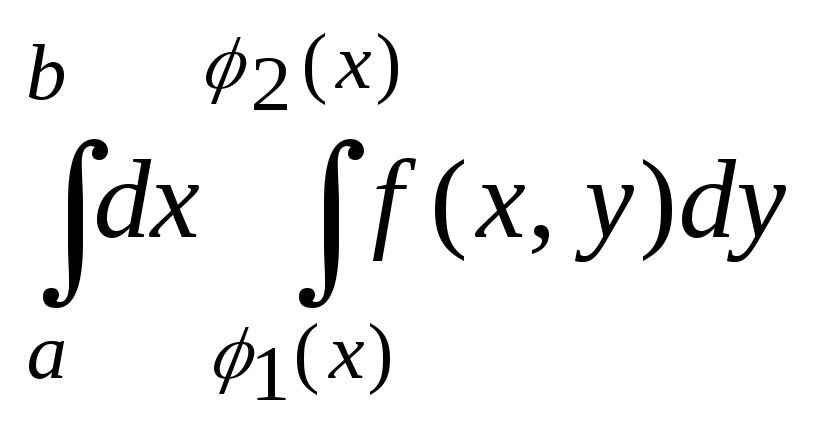 .
.
Двойной интеграл
по области
![]() вычисляется по формуле
вычисляется по формуле
![]()
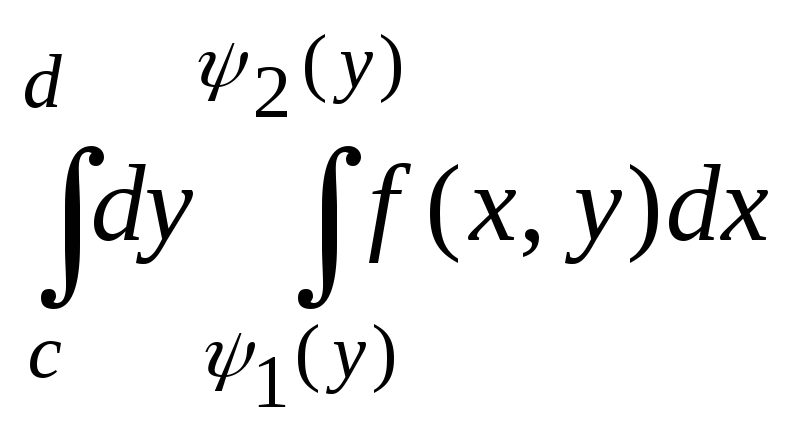 .
.
Если
![]() не является множеством такого вида, то
её представляют в виде объединения
непересекающихся (без общих внутренних
точек) областей
не является множеством такого вида, то
её представляют в виде объединения
непересекающихся (без общих внутренних
точек) областей![]() ,
каждая из которых является элементарной
в направлении той или другой оси.
Разбиение зависит от желаемого порядка
расстановки пределов интегрирования.
Тогда в силу аддитивности двойного
интеграла
,
каждая из которых является элементарной
в направлении той или другой оси.
Разбиение зависит от желаемого порядка
расстановки пределов интегрирования.
Тогда в силу аддитивности двойного
интеграла![]()
![]() .
.
В задачах
10.17-10.26 вычислить
следующие двойные интегралы по областям
![]() ,
ограниченным указанными линиями:
,
ограниченным указанными линиями:
10.17 ,,,.
10.18
![]() ,
,![]() ,
,![]() .
.
10.19
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.20
![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
10.21
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.22
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.23![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.24![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.25
![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
10.26
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
При переходе в
двойном интеграле от прямоугольных
координат
![]() к
полярным координатам
к
полярным координатам![]() ,
связанным с
прямоугольными координатами соотношениями
,
связанным с
прямоугольными координатами соотношениями
![]() ,
,![]() ,имеет место
формула
,имеет место
формула
![]()
![]() ,где
,где
![]() - область интегрирования в плоскости
переменных
- область интегрирования в плоскости
переменных![]() и
и![]() .
.
Если область
![]() имеет вид
имеет вид![]() ,
где функции
,
где функции![]() ,
,![]() - непрерывны и заданы одним аналитическим
выражением на отрезке
- непрерывны и заданы одним аналитическим
выражением на отрезке![]() ,
то двойной интеграл
,
то двойной интеграл
![]() ,где
,где
![]() ,вычисляется
по формуле
,вычисляется
по формуле
![]()
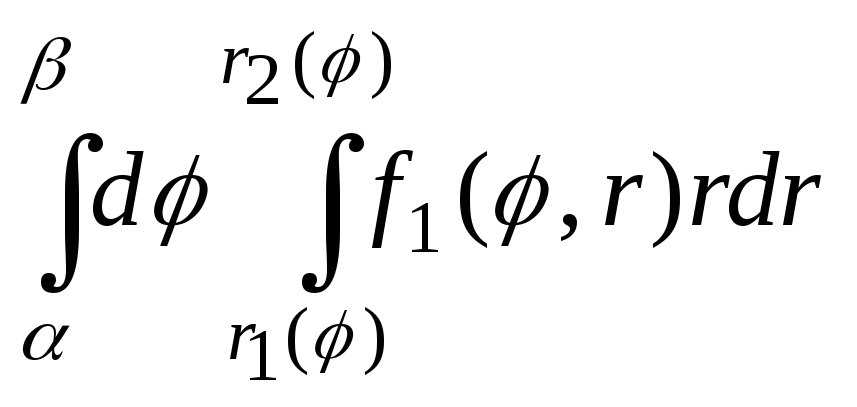 .
Если область интегрирования
.
Если область интегрирования![]() не принадлежит к рассмотренному виду,
то её разбивают на части, каждая из
которых является областью данного вида.
не принадлежит к рассмотренному виду,
то её разбивают на части, каждая из
которых является областью данного вида.
В задачах
10.27-10.32 в
двойном интеграле
![]() перейти к полярным координатам (
перейти к полярным координатам (![]() )
и расставить пределы интегрирования,
если:
)
и расставить пределы интегрирования,
если:
10.27 .
10.28
![]()
![]() .
.
10.29
![]() .
.
10.30
![]() .
.
10.31
![]()
![]() .
.
10.32
![]() .
.
В задачах 10.33-10.42 перейти к полярным координатам и вычислить следующие двойные интегралы:
10.33
![]() ,
,![]() .
.
10.34![]() ,
,
![]() .
.
10.35![]() ,
,![]() .
.
10.36![]() ,
,![]() .
.
10.37![]() ,
,![]() .
.
10.38![]() ,
,![]() .
.
10.39![]() ,
,![]() .
.
10.40![]() ,
,![]() .
.
10.41
![]() ,
,![]() .
.
10.42![]()
§2. Некоторые приложения двойного интеграла.
Площадь области
![]() вычисляется по формуле
вычисляется по формуле![]() .
При переходе в двойном интеграле от
прямоугольных координат
.
При переходе в двойном интеграле от
прямоугольных координат![]() к полярным координатам
к полярным координатам![]() ,
имеет место формула
,
имеет место формула![]()
![]() ,где
,где
![]() - область интегрирования в плоскости
переменных
- область интегрирования в плоскости
переменных![]() и
и![]() .
.
Среднее значение
непрерывной функции
![]() в
области
в
области
![]() вычисляется по формуле
вычисляется по формуле![]() .
.
В задачах
10.43-10.48 найти
площадь области
![]() ,
ограниченной указанными линиями:
,
ограниченной указанными линиями:
10.43
![]() ,
,![]() .
.
10.44
![]() ,
,![]() ,
,![]()
![]() .
.
10.45
![]() ,
,![]() ,
,![]() .
.
10.46
![]() ,
,![]() .
.
10.47
![]() ,
,![]() .
.
10.48
![]() ,
,![]() ,
,![]() ,
,![]() .
.
В задачах
10.49-10.52 используя
полярные координаты, найти площадь
области
![]() ,
ограниченной указанными линиями:
,
ограниченной указанными линиями:
10.49
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.50
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.51
![]() ,
,![]()
![]() .
.
10.52
![]() ,
,![]()
![]() (
(![]() ).
).
В задачах
10.53-10.56 найти
среднее значение функции
![]() в области
в области![]() ,
ограниченной указанными линиями, если:
,
ограниченной указанными линиями, если:
10.53
![]()
![]() ,
,![]() ,
,![]() .
.
10.54
![]()
![]() ,
,![]() ,
,![]() .
.
10.55
![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.56
![]()
![]() .
.
Объём υ
цилиндроида,
ограниченного сверху непрерывной
поверхностью
![]() ,
снизу плоскостью
,
снизу плоскостью![]() и с боков прямой цилиндрической
поверхностью, вырезающей на плоскости
и с боков прямой цилиндрической
поверхностью, вырезающей на плоскости![]() область
область![]() ,
вычисляется по формулеυ
,
вычисляется по формулеυ![]() .
При переходе в двойном интеграле от
прямоугольных координат
.
При переходе в двойном интеграле от
прямоугольных координат![]() к полярным координатам
к полярным координатам![]() ,
имеет место формулаυ
,
имеет место формулаυ![]() ,где
,где
![]() - область интегрирования в плоскости
переменных
- область интегрирования в плоскости
переменных![]() и
и![]() .
.
В задачах
10.57-10.62 найти
объёмы тел
![]() ,
ограниченных следующими поверхностями:
,
ограниченных следующими поверхностями:
10.57
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.58
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.59
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.60
![]() ,
,![]() ,
,![]() .
.
10.61
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.62
![]() ,
,![]() ,
,![]() .
.
В задачах
10.63-10.66 перейти
к полярным координатам и найти объёмы
тел
![]() ,
ограниченных поверхностями:
,
ограниченных поверхностями:
10.63
![]() ,
,![]() ,
,![]() ,
,![]() .
.
10.64
![]() ,
,![]() .
.
10.65
![]() ,
,![]() ,
,![]() .
.
10.66
![]() ,
,![]() .
.
Если
![]() - область плоскости
- область плоскости![]() ,
занятая пластинкой, и
,
занятая пластинкой, и![]() -
плотность пластинки, то статические
моменты
-
плотность пластинки, то статические
моменты![]() и
и![]() ,
моменты инерции
,
моменты инерции![]() и
и![]() относительно осей
относительно осей![]() и
и![]() ,
масса
,
масса![]() ,
координаты
,
координаты![]() и
и![]() центра масс
центра масс![]() пластинки
пластинки![]() вычисляются по формулам:
вычисляются по формулам:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
Если пластинка
однородная, то полагают
![]() .
.
В задачах
10.67-10.70 найти
массу пластинки плотности
![]() ,
ограниченной указанными линиями:
,
ограниченной указанными линиями:
10.67
![]() ,
,![]() ,
,![]()
![]() ,
,
![]() .
.
10.68
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
10.69![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
.
10.70
![]() ,
,![]() ,
,![]()
![]() ,
,
![]() .
.
10.71 Найти
массу круглой пластинки радиуса
![]() ,
если плотность её
,
если плотность её![]() пропорциональна квадрату расстояния
точки от центра и равна
пропорциональна квадрату расстояния
точки от центра и равна![]() на краю пластинки.
на краю пластинки.
10.72 Плоское
кольцо ограничено двумя концентрическими
окружностями, радиусы которых равны
соответственно
![]() и
и![]() .
Зная, что плотность материала
.
Зная, что плотность материала![]() пропорциональна расстоянию от центра
окружностей, найти массу кольца, если
плотность на окружности внутреннего
круга равна
пропорциональна расстоянию от центра
окружностей, найти массу кольца, если
плотность на окружности внутреннего
круга равна![]() .
.
10.73 Найти
статические моменты следующих однородных
плоских фигур (плотность
![]() ):
):
а) прямоугольника
со сторонами
![]() и
и![]() относительно
стороны
относительно
стороны![]() ;
;
б) полукруга
радиуса
![]() относительно диаметра;
относительно диаметра;
в) круга
радиуса
![]() относительно касательной;
относительно касательной;
г)
четверти эллипса с полуосями
![]() и
и![]()
![]() относительно полуоси
относительно полуоси![]() .
.
В задачах
10.74-10.77 найти
координаты центра масс однородной
пластинки плотности
![]() ,
ограниченной линиями:
,
ограниченной линиями:
