
GOSI 2 / ТАУ / Не нужное / Теория автоматического управления / 2.Устойчивость линейных систем / Устойчивость линейных систем
.docУТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ.
(алгебраический критерий)
Для того, чтобы любая система могла быть использована - она должна быть прежде всего устойчива.
Устойчивость - способность системы приходить в установившееся состояние (обычно нулевое) при снятии всех воздействий.
Y(t) = Yk(t) + Yсв(t);
Yсв(t) - свободное движение (описывается свойствами системы)
Yk(t) - описываются действиями воздействий.
При отсутствии воздействий на систему
Y(t) = Yсв(t).
lim Yсв(t) -> 0,
при t -> (бесконечность).
Свободное состояние описывается дифференциальным уравнением:
d^(n)Yсв d^(n-1)Yсв dYсв
Ao * -------- + A1 * ---------- + ... + A(n-1) * ---- + An * Yсв = 0
dt^(n) dt^(n-1) dt
1) Если характеристическое уравнение системы имеет только вещественные корни, то:
n ai*t
Yсв(t) = E Ai*e
i=1
здесь:
ai - корни характеристического уравнения (вещественные);
Ai - определяются свойствами системы и начальными условиями;
Условие устойчивости: все корни < 0.
2) Если характеристическое уравнение системы имеет только комплексные корни, то есть: X1=a+jb и X2=a-jb;
n ai*t ai*t
Yсв(t)=E [ Ai*e + e * cos(b*t + f)];
i=1
Для устойчивости характеристического уравнения необходимо, чтобы ai < 0.
При наличии нулевого корня в состоянии свободного движения появляется постоянная составляющая и условия устойчивости не будут соблюдаться.
Если есть пара мнимых корней, то условие устойчивости соблюдаться не будет.
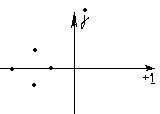
Таким образом, необходимым и достаточным условием устойчивости является то, что все вещественные корни должны быть отрицательны и также отрицательны вещественные части комплексных корней.
Если корни на комплексной плоскости, то они должны быть слева от мнимой оси. (см. пример на картинке)
Мнимая ось - граница устойчивости. Если корни на оси, то система на границе устойчивости:
- если нулевые корни, то на границе апериодической устойчивости;
- если корни чисто мнимые, то на границе колебательной устойчивости;
Таким образом, для определения устойчивости системы достаточно знать знаки корней характеристического уравнения.
Судить о знаках позволяет критерий устойчивости, который не требует нахождения самих корней.
КРИТЕРИЙ УСТОЙЧИВОСТИ ГУРВИЦА
(алгебраический критерий)
Используется для определения устойчивости разомкнутых и замкнутых систем при помощи так называемых определителей Гурвица и может быть просто использовано для систем до 5-ого порядка.
n n-1
Со* p + C1* p +...+ C(n-1)* p + Cn = 0;
|C1 C3 … 0|
|C0 C2 … 0|
|0 C3 … 0|
|…………………….. 0|
|0 0 ..…...Cn|
Для устойчивости необходимо и достаточно, чтобы при положительных коэффициентах характеристического уравнения все n определителя Гурвица.
n - порядок характеристического уравнения.
ПРИМЕРЫ:
1) Дано: Со * p + C1 = 0;
C1 = д1 > 0;
при Сi>0 -> устойчива система.
2
2) Дано: Со* p + C1 * p + C2 = 0;
|C1 0 | д1 = С1 >0;
|Co C2| д2 = C1 * C2 > 0;
при Сi>0 -> устойчива система.
3 2
3) Дано: Co*p + C1*p + C2*p + C3 = 0;
|C1 C3 0 | д1 = C1>0;
|Co C2 0 | д2 = С1*С2 - Со*С3 > 0;
|0 C1 C3| д3 = С3* д2;
Для устойчивости надо: Сi>0 и д2>0;
КРИТЕРИЙ РАУСА
(частотный критерий)
Может использоваться для разомкнутых и замкнутых систем любого порядка с использованием таблицы Рауса. Удобен для ЭВМ. Позволяет определить количество нулевых и чисто мнимых корней, а также количество правых корней.
Таблица Рауса:
--------------------------------------
Вспом.| № | N столбца |
коэф. |стр| 1 | 2 | 3 |
--------------------------------------
| 1 |a11=Co |a12=C2 |a13=C4 |
| 2 |a21=C1 |a22=C3 |a23=C5 |
a11| | | | |
r3=---| 3 |a31=a12-|a32=a13-|a33=a14-|
a21| | -r3*a22| -r3*a23| -r3*a24|
| | | | |
a21| | | | |
r4=---| 4 |a41=a22-|a42=a23-|a43=a24-|
a31| | -r4*a32| -r4*a33| -r4*a34|
.....................................
1-ая строка :четные коэффициенты (0,2,4...)
2-ая строка :нечетные коэффициенты (1,3,5...)
Для устойчивости системы необходимо и достаточно чтобы все коэффициенты 1-ого столбца таблицы имели один знак.
В случае, если интересует только устойчивость, то как только найден первый коэффициент с '-'-ым знаком в 1-ом столбце.
Часто нужно знать количество корней, мнимых, нулевых. Тогда нужно считать до конца.
a) Количество корней с '-'-ым знаком в 1-ом столбце - число правых корней;
б) Если в середине таблицы нули, то соответствует паре чисто мнимых корней. Количество нулей в конце 1-ого столбца - количество нулевых корней.
То есть, можно получить полную картину корней характеристического уравнения.
КРИТЕРИЙ МИХАЙЛОВА
(частотный критерий)
Может использоваться для анализа устойчивости как разомкнутых, так и замкнутых систем с построением годографа Михайлова на комплексной плоскости, позволяет определять наличие нулевых корней и количество правых корней, если таковые имеются.
Пригоден для ЭВМ.
n n-1
D(p) = Co*p +C1*p +...+ C(n-1)*p +Cn = 0
при p -> jw, тогда
D(jw) = X(w) + j Y(w);
2 4
X(w)=Cn- C(n-2)*w + C(n-4)*w - .... ;
3 5
Y(w)=C(n-1)*w-C(n-3)*w +C(n-5)*w -....;
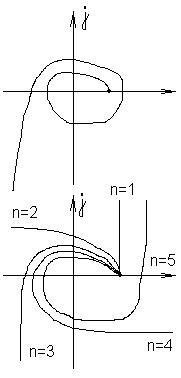
Меняя w = от 0 до бесконечности получим кривую - это есть годограф Михайлова.
Для устойчивости системы необходимо и достаточно, чтобы годограф при w = 0..(бесконечность), начинался на '+'-ой полуоси комплексной плоскости, последовательно обходил в '+'-ом направлении, нигде не обращаясь в нуль 'n' квадрантов, где n - порядок уравнения.
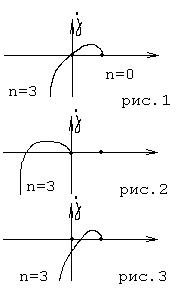
На границе устойчивости (пара чисто мнимых корней) (см. рис. 1)
На границе устойчивости (нулевой корень) (см. рис. 2)
Не устойчива (положительные корни) Число положительных корней определяется по формуле:
a = n*pi/2 - l*pi;
l -число правых корней;
Например, (см. рис. 3)
a = -pi/2 ;тогда l=2; то есть,
два положительных корня.
Критерий Найквиста
(частотный критерий)
Используется только для определения устойчивости замкнутых систем с использованием частотных характеристик разомкнутых систем. То есть, при применении метода приходится определять устойчивость разомкнутой системы и если она не устойчива, то определить число правых корней.
Используется для анализа устойчивости замкнутой ф-ии для АФЧХ разомкнутой системы.
Wраз(p)
Ф(p) = ----------- ; Wраз(p) = -1;
1 + Wраз(p)
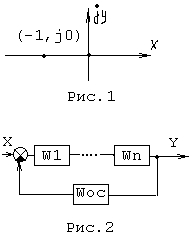
Очевидно, что если разомкнутая система состоит из последовательной цепочки типовых звеньев , то структурная схема будет выглядит на рис. 2 без ОС.
"Характеристическое уравнение" = "знаменатель П.Ф."
Если же цепочки, охватываемые ОС, то определение корней не так просто...
Критерии устойчивости:
1) Разомкнутая система устойчива.
Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении w = 0 .. (бесконечность), не охватывала точку (-1,j0).
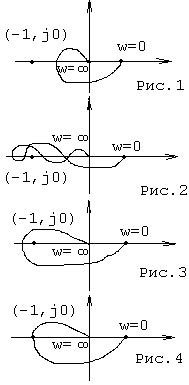
См. рис. 1 и 2. Обе системы устойчивы, но при некоторых изменениях коэффициентов может произойти изменение АФЧХ, во 2-ом случае - может стать неустойчивой. Пример неустойчивой системы на рис.3. На границе устойчивости на рис.4
2) Разомкнутая система на границе устойчивости.
То есть, АФЧХ раз. системы находится в бесконечности.
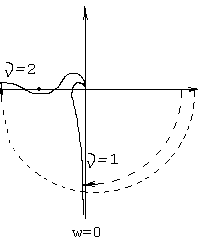
а) Если система имеет нулевые корни. В зависимости от количества нулевых корней АФЧХ - в соответствующем квадранте и АФЧХ надо дополнить дугой радиусом, равным бесконечности, которая начинается на вещественной оси и поворачивается на угол "90" по часовой стрелке. См. рисунок (система устойчива).
б) Если имеются чисто мнимые корни. При этом АФЧХ имеет разрыв. Тогда дополняем дугой бесконечного радиуса.
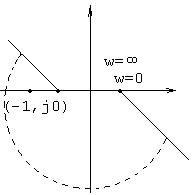
Во всех этих случаях для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы, дополненная дугами бесконечного радиуса НЕ охватывала точку (-1, j0).
Пример на рисунке - не устойчива система.
3) Разомкнутая система неустойчивая. Наряду с вещественными положительными корнями, могут иметься и чисто мнимые корни; таким образом, дополняем дугами R=(бесконечность) и АФЧХ рассматривается с этими дугами целиком.
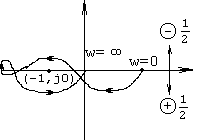
Пример на рисунке. В этом случае, чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы вектор, начало которого находится в точке (-1,j0), а конец скользит по АФЧХ, поворачивается на угол L*180 градусов в положительном направлении при изменении w = 0..(бесконечность).
Правило перехода: считается количество переходов вещественной полуоси от -1 до -(бесконечность) при w = 0..(бесконечность).
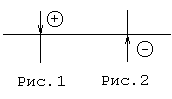
При этом, переход '+'-ый, если "проходит вниз" сквозь полуось.(рис.1)
Переход '-'-ый, если "проходит вверх" сквозь полуось.(См. рис.2)
Если АФЧХ начинается или заканчивается на этой оси, то считается 1/2 перехода.
Для устойчивости замкнутой системы необходимо и достаточно чтобы число переходов вещественной полуоси от -1 до -(бесконечность) в '+'-ом направлении было на l/2 больше, чем в '-' при w = 0..(бесконечность).
То есть, в данном способе (пример на рисунке) система будет устойчива, если она имеет 2 правых корня. При этом l/2=1.

Для практического применения существует логарифмический анализ критерия Найквиста, который основан на анализе ЛАХ и ЛФХ.
Рассмотрим его далее:
Устойчивость определяется относительно линии "-180" градусов. Для устойчивости замкнутой системы необходимо и достаточно, чтобы число '+'-ых переходов ФЧХ линии "-180" было на l/2 больше, чем '-'-ых переходов в диапазоне, где ЛАХ > 0.
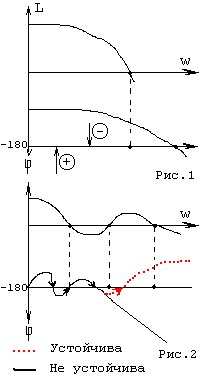
Если разомкнутая система устойчива, то линия не должна пересекать или число переходов - равно.
