GOSI 2 / ТАУ / Не нужное / Теория автоматического управления / 8.Метод гармонической линеаризации. Вибрационная линеаризация / Метод гармонической линеаризации

43. Метод гармонической линеаризации.

Применяется тогда, когда мы можем считать что на выходе нелинейной системы имеются гармонические колебания с постоянной амплитудой и частотой (имеются автоколебания).

Метод не имеет ограничение на порядок. В системе могут присутствовать сразу несколько нелинейностей. Этот метод может быть использован для нелинейных дифференциальных уравнений.

Положим, что на входе мы имеем sin колебания с амплитудой а и частотой .

(1)

ЛЧ – является фильтром высоких частот.

- разложение в ряд Фурье.

(2)

Положим что это имеет место всегда, если мы рассматриваем симметричную нелинейность, а так же, если на вход не поступает возмущающее воздействие.

Из (1) следует

Подставим в (2) и пренебрежем высшими гармониками

где

Таким образом вместо нелинейного уравнения получено линеаризованное уравнение. Такое преобразование называется гармонической линеаризацией, а коэффициенты называются коэффициентами гармонической линеаризации.

Из последнего уравнения можно получить передаточную функцию:

Чтобы характеристическое уравнение соответствовало случаю наличия автоколебаний, это уравнение должно иметь пару чисто мнимых корней.

47. Вибрационная линеаризация некоторых нелинейностей.

Если на вход нелинейного элемента подать постоянное или медленно изменяющееся воздействие и некоторую периодическую составляющую, частота которой значительно выше, то на выходе нелинейного элемента мы получим выходной сигнал который состоит из медленно изменяющегося y₀ и периодической составляющей y_n.

Таким образом, подавая на вход нелинейного элемента сигнал, мы можем существенно изменять его характеристику.

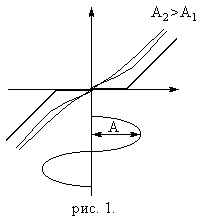
По мере роста амплитуды нелинейная характеристика сужается (рис. 1.).

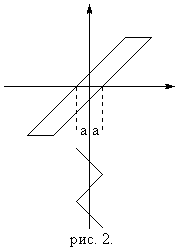
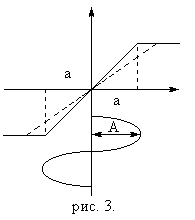
При А = а петля сужается в два раза. Если А = 2а то петля заменяется прямой (рис. 2.).

Если автоколебания в системе допустимы, то эти автоколебания могут сыграть положительную роль с точки зрения влияния нелинейности на характеристики системы.