Строительная механика / Учебник СМ Саргсян / П18

7.10. Изгиб тонкостенной цилиндрической оболочки при симметричном нагружении

В декартовой системе координат x, y, z, рассмотрим тонкостен­ный цилиндр радиуса R и постоянной толщины h при действии осесимметричной нагрузки (рис. 7.22). В данном случае очевидно, что деформации и напряжения, возникающие в оболочке также обладают осевой симметрией.

Обозначим через w радиальное перемещение, а через j угол на­клона касательной к образующей срединной поверхности цилиндра (рис. 7.23).

`В данном случае

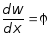. (7.59)

Относительное удлинение e_x отрезка АВ, расположенного на расстоянии z от срединной поверхности (рис. 7.24), складывается из двух составляющих: из удлинения срединной поверхности и уд­линения, обусловленного искривлением образующей цилиндра рав­ному z . Полное удлинение отрезка АВ принимает значение:

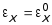+ z . (7.60)

Удлинение в окружном направлении:

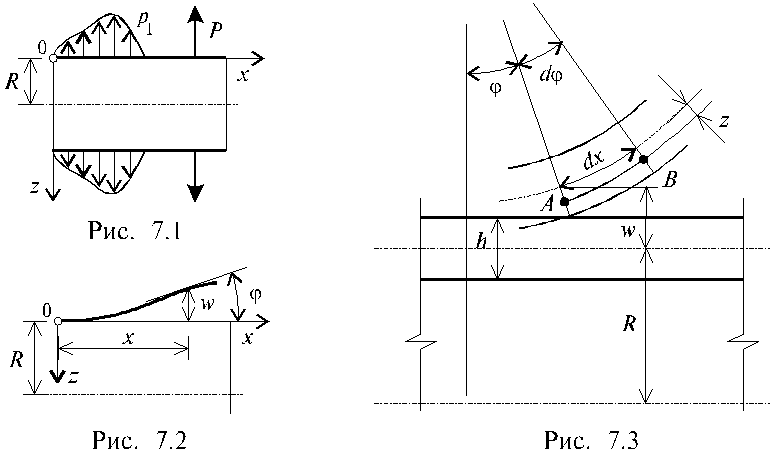
. (7.61)

Этим удлинениям соответствуют напряжения s_x и s_y , величи­ны которых по закону Гука определяются по формулам:

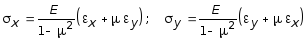. (7.62)

Рис. 7.25

С учетом (7.59) - (7.61) послед­ние формулы преобразуются к виду:

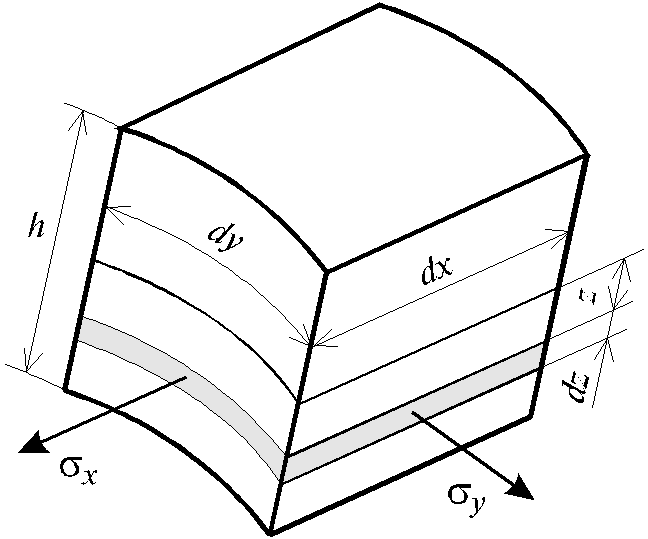
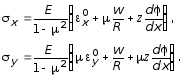(7.63)

В меридиональных и попе­речных сечениях цилиндра воз­никают моменты, поперечные и продольные силы. Значения мо­ментов и нормальный усилий яв­ляются результатом действия s_х и s_у . Для этого рассмотрим ма­лый элемент, выделенный из состава цилиндрической оболочки с размерами h, dx, dy (рис. 7.25). Нормальные силы на площадках h×dy и h×dx, отнесены к единице дуги сечения, определяются:

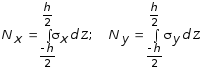. (7.64)

Величины моментов в тех же сечениях вычисляются:

. (7.65)

С учетом (7.59) и (7.63), выражения продольных сил и моментов, в зависимости от перемещения w, принимают вид:

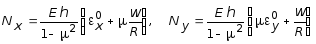; (7.66)

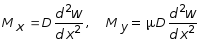, (7.67)

Рис. 7.26

где D - называется цилин­дрической жесткостью обо­лочки и определяется:

.

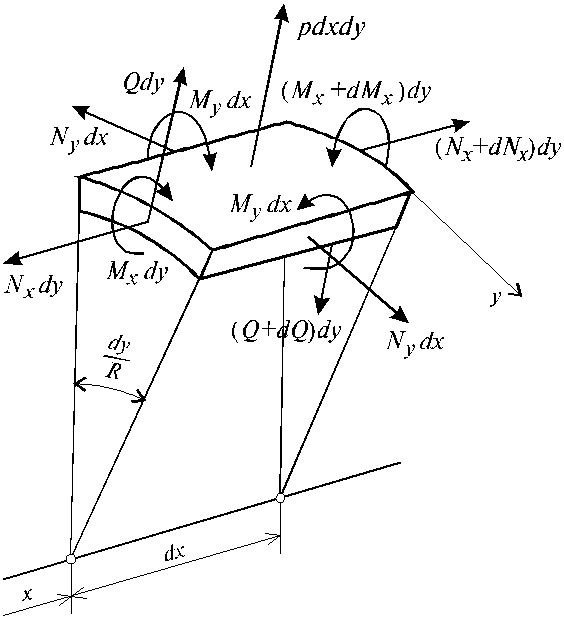
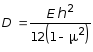Далее обратимся к урав­нениям равновесия, снова рассматривая элемент ци­линдрической оболочки с размерами h, dx, dy, и к его граням приложим равно­действующие силы и мо­менты, которые равны ве­личинам N_x, N_y, M_x, M_y, умноженные, соответствен­но на dx и dy (рис. 7.26). Кроме указанных силовых факторов, учитываем поперечную силу Q dy и внешние силы, обусловленные давлением P = P(x).

Здесь необходимо учесть, что при переходе от грани малого элемента с координатой х к грани с координатой x + dx, усилия получают соответствующие приращения. В осевых сечениях по свойствам симметрии конструкции и внешних нагрузок внутренние силовые факторы остаются одинаковыми. Проектируя силы на ось цилиндра, получим:

Это значит, что осевая сила N_x определяется из граничных ус­ловий нагружения цилиндра на торцах и она всегда определяется самостоятельно. Поэтому в дальнейшем будем считать эти условия заданными, а силу N_x - известной.

Проектируя все внешние и внутренние силы на радиальном направлении, получим второе уравнение равновесия:

,

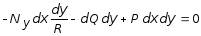откуда

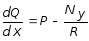. (7.68)

Третье уравнение равновесия получаем, приравнивая нулю сум­му моментов всех усилий относительно оси y, касательной к дуге нормального сечения:

,

или

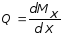. (7.69)

Вследствие осевой симметрии, остальные уравнения равновесия удовлетворяются тождественно.

Для дальнейшего преобразования полученных выражений, из (7.66 исключаем , а из (7.68) и (7.69) - поперечную силу Q. Вследствие чего, получим:

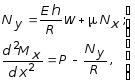(7.70)

и, исключая из этих уравнений N_y , будем иметь:

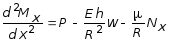. (7.71)

С учетом первого выражения (7.67), исключая изгибающий мо­мент из (7.71), получим уравнение относительно одной искомой ве­личины - перемещения w:

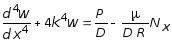, (7.72)

где

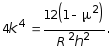
Из этого следует, что уравнение (7.72), к которому сводится решение поставленной задачи, структурно совпадает с уравнением (3.4), которое было получено при рассмотрении изгиба балки на упругом основании.

Родственность этих задач неоспорима. Так как цилиндрическую оболочку можно рассматривать, как совокупность изгибающих по­лосок, связанных между собой упругими связями. При симметрич­ном нагружении все полоски изгибаются одинаково, и радиальная сила N_y в каждом сечении, как и для балки на упругом основании прямо пропорциональна местному прогибу w.

Для расчета прочности цилиндрической оболочки наибольшие напряжения определяются выражениями (7.63) при

,

.

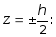
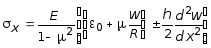С помощью (7.66), (7.67) последнее выражение преобразуется в виде:

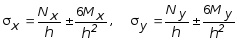. (7.73)

Таким образом, через перемещения w выражаются все внутрен­ние усилия и напряжения.

Для определения w рассмотрим решение уравнения (7.72), за­писывая его в виде:

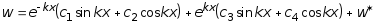, (7.74)

где - частное решение, которое определяется в зависимости от заданного закона изменения внешней нагрузки Р(х) вдоль образу­ющей.

Произвольные постоянные с_i (i = 1,2,3,4) определяются из кон­цевых условий закрепления цилиндра.

7.11. Расчет длинной цилиндрической трубы при действии внутреннего давления (задача 22)

Для цилиндрической трубы (рис. 7.27) большой длины , имею­щей на концах жесткие фланцы, при действии внутреннего давле­ния р, требуется:

1. Определить эпюры изгибающих моментов и прогибов w в ок­рестности фланцев;

2. Определить максимальные напряжения в окрестности флан­цев.

Решение

1. Определить эпюры изгибающих моментов и прогибов w в окрестности фланцев

В данном случае справедливо предположить, что осевая сила N_x равна нулю.

Так как давление р постоянно по оси х, то частное решение уравнения (7.72) принимает вид:

.

Подставляя выражение в (7.74), получим:

.

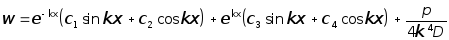При достаточно большом расстоянии от фланца x ³  перемещение w должно стремиться к постоянной величине. Этому условию противоречит наличие слагаемого , которое неограниченно возрастает с ростом х. Поэтому для устра­нения данного противоречия справедливо полагать, что с₃ = с₄ = 0. С учетом данного обстоятельства получим:

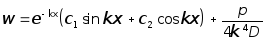. (7.75)

Для определения с₁ и с₂, учитывая, что в начале системы коор­динат при x = 0, в месте сопряжения цилиндра с жестким фланцем должно выполняться условие:

w = 0;    . (7.76)

Подставляя решение (7.75) в граничные условия (7.76) получим:

.

Рис. 7.27 Рис. 7.28

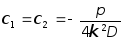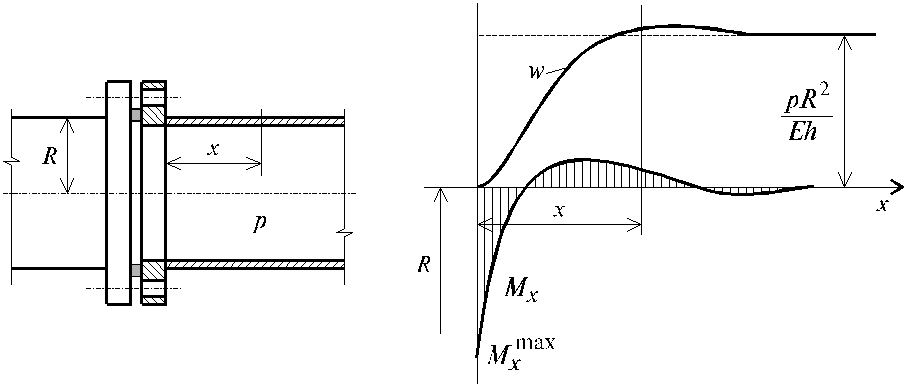
C учетом последнего выражения, решение (7.75) принимает вид:

.

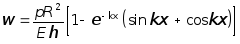При достаточно больших x ³  выражение преобразуется и приобретает вид:

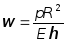. (7.77)

Подставляя (7.77) в (7.67), получим выражение для определения изгибающего момента М_х в следующем виде:

. (7.78) (7.20)

Эпюра М_х и график изменения w (x) изображен на рис. 7.28. Наибольшее значение изгибающий момент имеет в заделке, значение которого определяются из (7.78), полагая что х = 0:

.

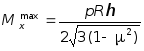2. Определить максимальные напряжения в окрестности фланцев

Поскольку N_x = 0, формула по определению меридионального напряжения s_х, из (7.73) принимает вид:

.

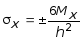Следовательно, максимальное напряжение вычисляется по фор­муле:

,

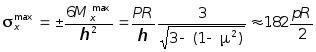т.е. изгибающие напряжения в меридиональном направлении ока­зываются в 1.82 раза больше расчетного напряжения по безмомент­ной теории, что подтверждает факт о неприменимости безмомент­ной теории в случаях когда оболочка имеет краевой эффект.

7.12. Расчет вертикально стоящего открытого цилин­дрического бака, заполненного доверху жидкостью (задача 23)

Пусть открытый цилиндрический бак, заделан нижней частью в жесткое основание и заполнен доверху жидкостью (рис. 7.29), тогда при следующих исходных данных: R = 1.0 м - радиус срединной поверхности цилиндра; h = 5×10^-3 м - толщина стенки цилиндра; H = 5 м - высота стенки бака; Е = 2×10⁸ кН/м² - модуль упругости материала конструкции; m = 0.3 - коэффициент Пуассона материа­ла; g = 10 кН/м³ - удельный вес жидкости, требуется:

1. Определить функции внутренних силовых факторов;

2. Построить эпюры М_х и N_y;

3. Определить эквивалентное напряжение по теории наиболь­ших касательных напряжений в опасных точках опасного сечения.

Pешение

1. Определить функции внутренних силовых факторов

Если координату х отсчитывать от днища цилиндра, то давле­ние от жидкости, заполняющей цилиндр, на стенки конструкции принимает значение:

р = g (H - x).

Очевидно, что при этом продольные силы по оси х, т.е. N_x = 0. Согласно (7.16) выражение перемещения w записывается в виде:

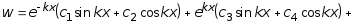
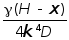+. (7.79)

256