
несобственные интегралы
.docxНесобственные интегралы I рода
Пусть ![]() определена
и непрерывна на множестве от
определена
и непрерывна на множестве от ![]() и
и  .
Тогда:
.
Тогда:
-
Если
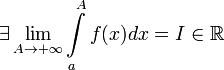 ,
то используется обозначение
,
то используется обозначение 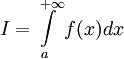 и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае 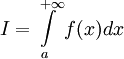 называется
сходящимся.
называется
сходящимся. -
Если не существует конечного
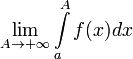 (
(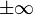 или
или 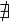 ),
то интеграл
),
то интеграл 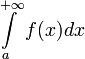 называется
расходящимся к
называется
расходящимся к 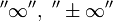 ,
или просто расходящимся.
,
или просто расходящимся.
Пусть ![]() определена
и непрерывна на множестве от
определена
и непрерывна на множестве от ![]() и
и 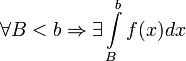 .
Тогда:
.
Тогда:
-
Если
 ,
то используется обозначение
,
то используется обозначение 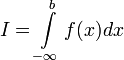 и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае 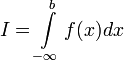 называется
сходящимся.
называется
сходящимся. -
Если не существует конечного
 (
(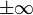 или
или  ),
то интеграл
),
то интеграл  называется
расходящимся к
называется
расходящимся к 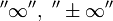 ,
или просто расходящимся.
,
или просто расходящимся.
Если
функция ![]() определена
и непрерывна на всей числовой прямой,
то может существовать несобственный
интеграл данной функции с двумя
бесконечными пределами интегрирования,
определяющийся формулой:
определена
и непрерывна на всей числовой прямой,
то может существовать несобственный
интеграл данной функции с двумя
бесконечными пределами интегрирования,
определяющийся формулой:
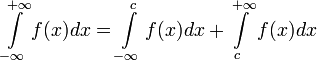 ,
где с — произвольное число.
,
где с — произвольное число.
[править]Геометрический смысл несобственного интеграла I рода
Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.
[править]Примеры

[править]Несобственные интегралы II рода
Пусть ![]() определена
на
определена
на ![]() ,
терпит бесконечный разрыв в точке x=a
и
,
терпит бесконечный разрыв в точке x=a
и 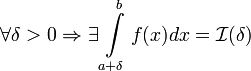 .
Тогда:
.
Тогда:
-
Если
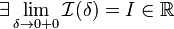 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся. -
Если
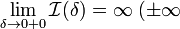 или
или 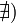 ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а 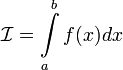 называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Пусть ![]() определена
на
определена
на ![]() ,
терпит бесконечный разрыв при x=b и
,
терпит бесконечный разрыв при x=b и 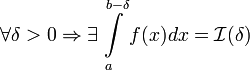 .
Тогда:
.
Тогда:
-
Если
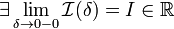 ,
то используется обозначение
,
то используется обозначение 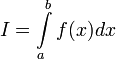 и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся. -
Если
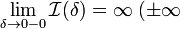 или
или 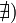 ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а 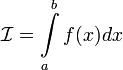 называется
расходящимся к
называется
расходящимся к 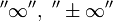 ,
или просто расходящимся.
,
или просто расходящимся.
Если
функция ![]() терпит
разрыв во внутренней точке
терпит
разрыв во внутренней точке ![]() отрезка
отрезка ![]() ,
то несобственный интеграл второго рода
определяется формулой:
,
то несобственный интеграл второго рода
определяется формулой:

[править]Геометрический смысл несобственных интегралов II рода
Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции
[править]Пример
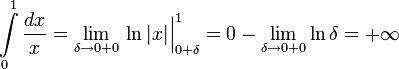
Несобственный
интеграл
с
несколькими особенностями .
Если
функция определена на интервале (a,b) и
неограниченна в точках a и b и при некотором
выборе точки с (a,b) существуют несобственные
интегралы на полуинтервалах (a,c]
и[c,b),c(a,b).
При
этом существование и значение данного
интеграла не зависит от выбора точки
с.Тогда
Y
.
f(x)
0
a k c l b X
Такие
интегралы называются несобственными
интегралами с двумя (или несколькими)
особенностями.(рисунок 2)
Вообще,если
функция f :R
имеет на промежутке конечное число
особых точек и Т: a=k1<k2< …….., что на
каждом из,i=1n,особой
точкой функции является только одна из
концевых точек. Тогда, если каждый из
интегралов (1) :
cходится,
то
c
ходится. Если хотя
бы один из (1) расходится,то и весь (2)
расходится.Действительно,расходимость
хотя бы одного из участников суммы (2)
означает,что данный интеграл (1) либо
имеет бесконечную величину ,либо не
имеет конкретного значения тем самым
обращая всю сумму (2) либо в бесконечность,либо
лишая ее конкретного
значения.
Y
f(x)
0
a=k1 k2………ki…….kn-1 kn=b(+
в данном случае).
Рис.,поясняющий
несобственный интеграл с несколькими
особенностями .
Пример1.
Несобственный
интеграл имеет две особенности : в точке
x=0 функция неограниченно возрастает
(собственная особая точка) ,при x
имеем интеграл по бесконечному
промежутку(несобственная особая точка).
Разобьём интервал интегрирования 0;+
так, чтобы на каждом промежутке
подынтегральная функция f(x) имела не
более одной особенности .Например,
(0;
1) и (1;+).
По
определению исходный интеграл
С
ходится
тогда,и только тогда , когда сходятся
оба интеграла
П
ервый из этих
интегралов расходится при p
1 , второй - при p 1
,таким образом , одновременно оба эти
интеграла не сходятся ни при каком
значении p .Итак , исходный интеграл
расходится при любом значении p .
</k2<>![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
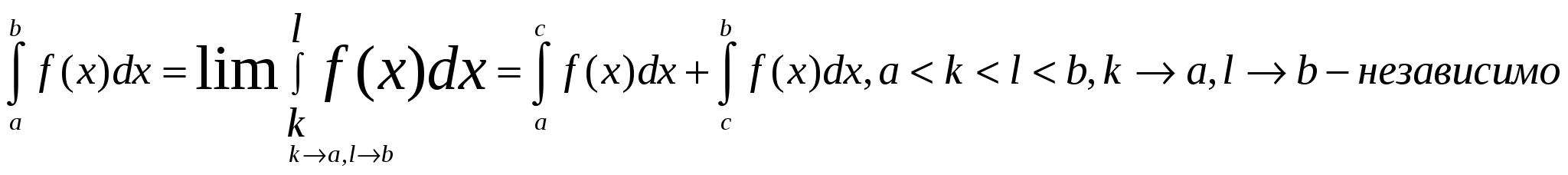
![]()
![]()

