
1396_49892_reshebnik / Задание / 2 Дифференцирование
.docПри необходимости более детального просмотра увеличьте масштаб документа!
www.otlichka.ru
§ 2.1. ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
-
Понятие производной. Производная функции
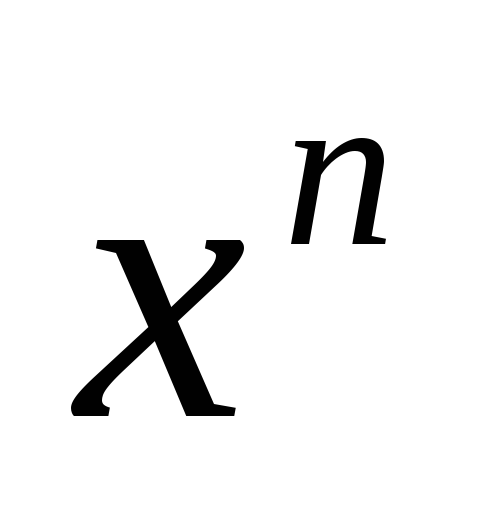 .
. -
Геометрический смысл производной. Уравнения касательной и нормали к графику функции.
-
Понятие дифференцируемости функции и дифференциала. Условие дифференцируемости. Связь дифференциала с производной.
-
Геометрический смысл дифференциала.
-
Непрерывность дифференцируемой функции.
-
Дифференцирование постоянной и суммы, произведения и частного.
-
Производная сложной функции.
-
Инвариантность формы дифференциала.
-
Производная обратной функции.
-
Производные обратных тригонометрических функций.
-
Гиперболические функции, их производные.
-
Производные высших порядков. Формула Лейбница. 13) Дифференциалы высших порядков. Неинвариантность дифференциалов порядка выше первого.
-
Дифференцирование функций, заданных параметрически.
$ 2.2. ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ
1) Исходя из определения производной, доказать, что:
а) производная периодической дифференцируемой функции есть функция периодическая;
б) производной четной дифференцируемой функции есть функция нечетная;
в) производная нечетной дифференцируемой функции есть функция четная.
-
Доказать, что если функция
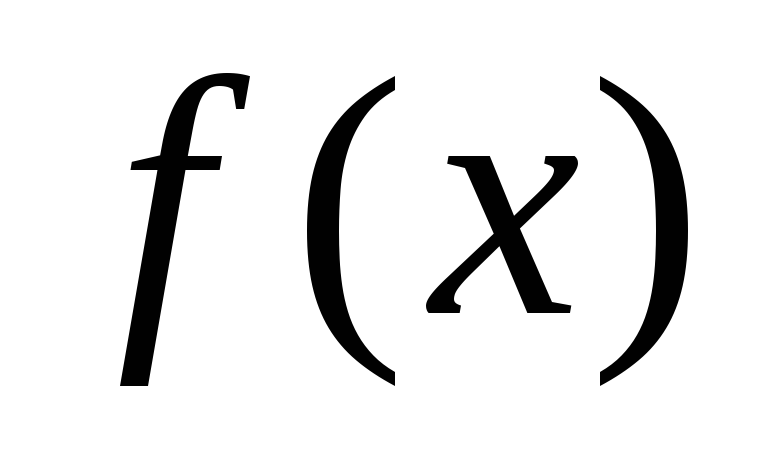 дифференцируема
в точке
х
= 0
и
дифференцируема
в точке
х
= 0
и
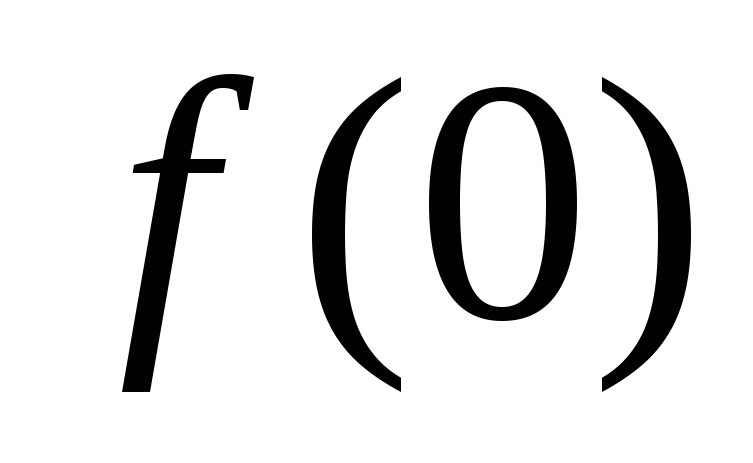 ,
то
,
то
![]()
-
Доказать, что производная
 не существует, если
не существует, если
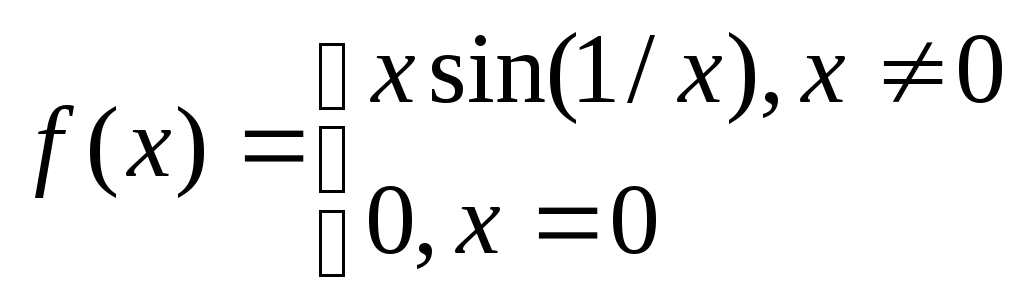
-
Доказать, что производная от функции
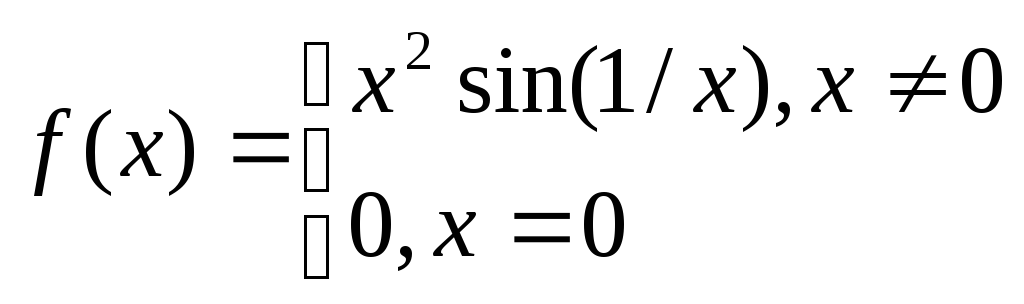
разрывна в точке х = 0.
5) Доказать приближенную формулу
![]()
6)
Что можно сказать о дифференцируемости
суммы
![]() в
точке
в
точке
![]() ,
если в этой точке:
,
если в этой точке:
а) функция
![]() дифференцируема,
а функция
дифференцируема,
а функция
![]() недифференцируема;
недифференцируема;
б) обе
функции
![]() и
и
![]() недифференцируемы.
недифференцируемы.
-
Пусть функция
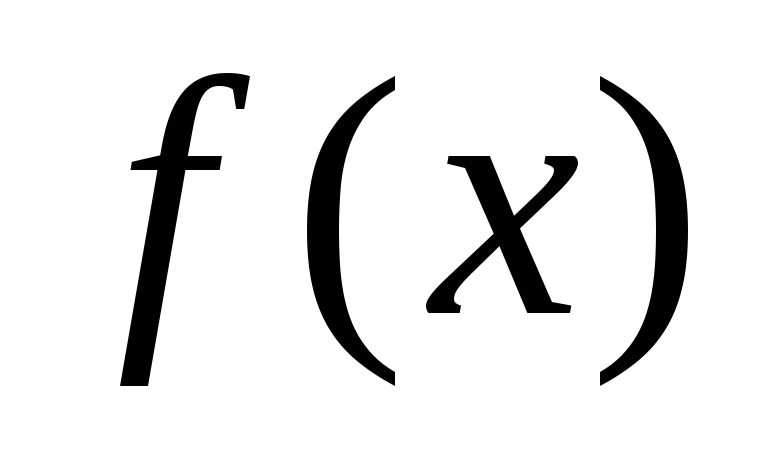 дифференцируема
в точке
дифференцируема
в точке
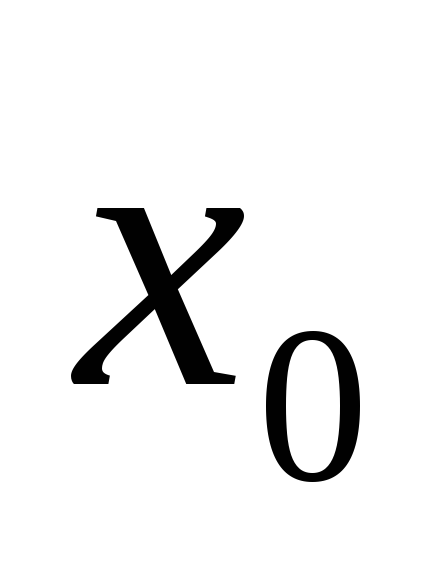 и
и
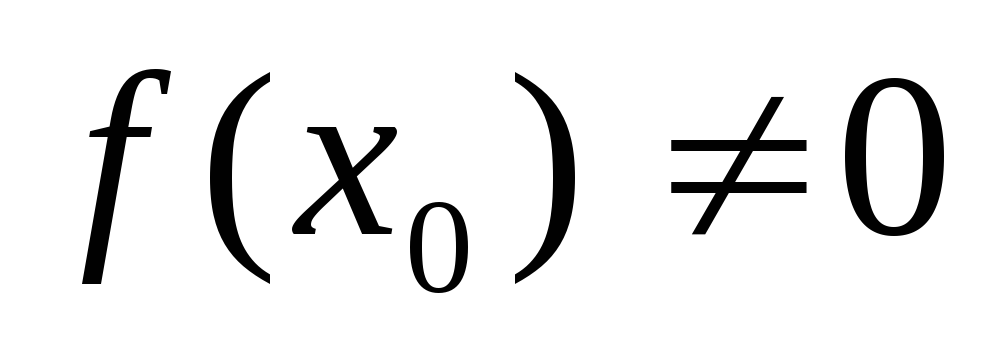 ,
а функция
,
а функция
 недифференцируема
в этой точке. Доказать,
что произведение
недифференцируема
в этой точке. Доказать,
что произведение
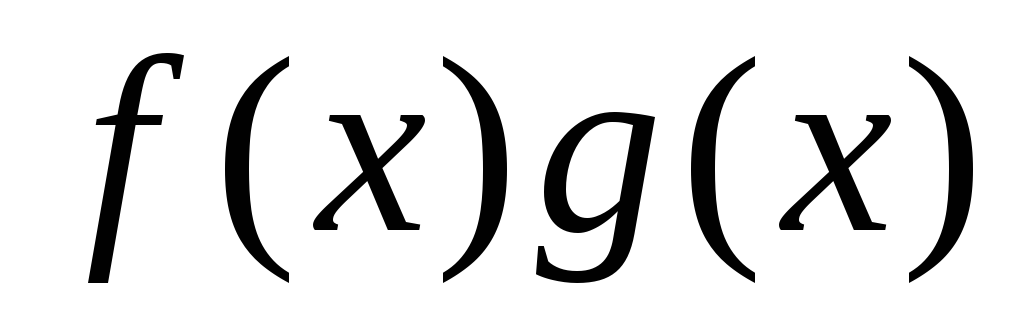 является
недифференцируемым
в точке
является
недифференцируемым
в точке
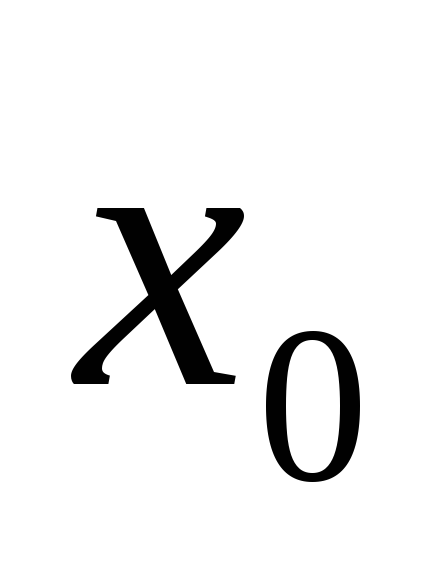
-
Что можно сказать о дифференцируемости произведения
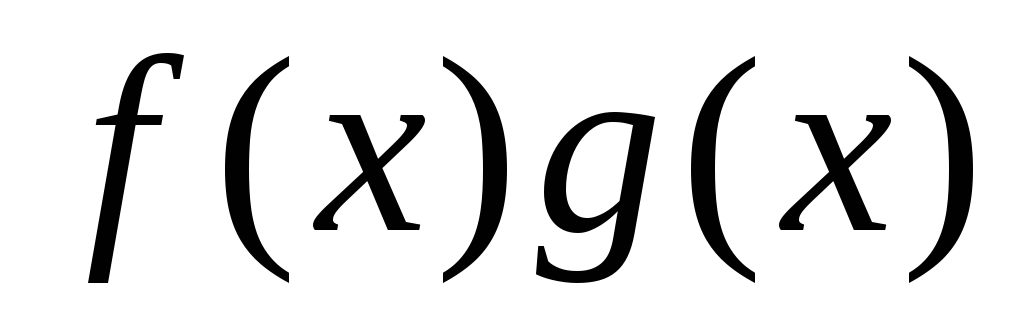 в
предположениях задачи 6?
в
предположениях задачи 6?
Рассмотреть примеры:
![]()
![]()
![]()
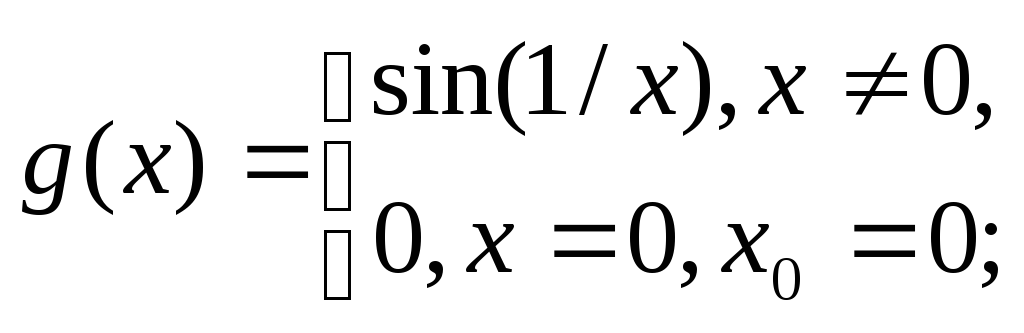
![]()
![]()
![]()
![]()
9)
Найти
![]() ,
если
,
если
![]()
10)
Выразить дифференциал
![]() от
сложной функции
от
сложной функции
![]() через
производные от функции
через
производные от функции
![]() и
дифференциалы
от функции
и
дифференциалы
от функции
![]() .
.
-
Пусть
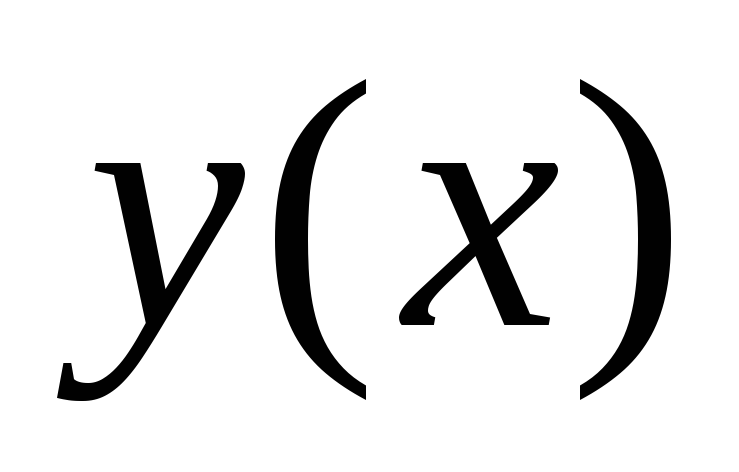 и
и
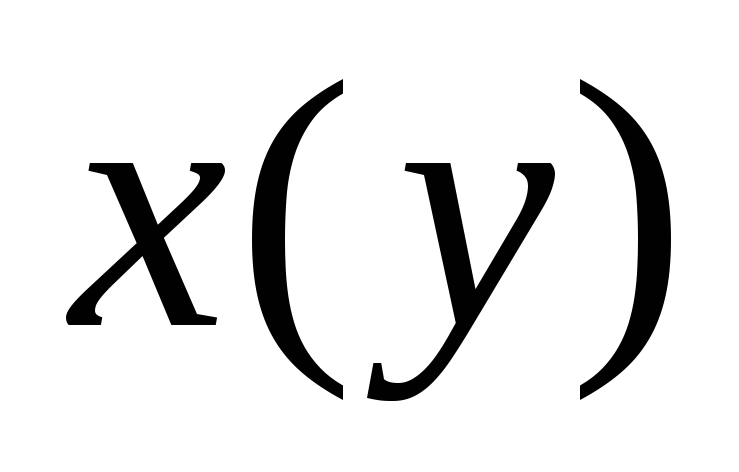 дважды
дифференцируемые взаимно обратные
функции. Выразить
дважды
дифференцируемые взаимно обратные
функции. Выразить
 через
через
 и
и
 .
.
§ 2.3. РАСЧЕТНЫЕ ЗАДАНИЯ
Задача
1. Исходя
из определения производной, найти
![]() .
.
1.
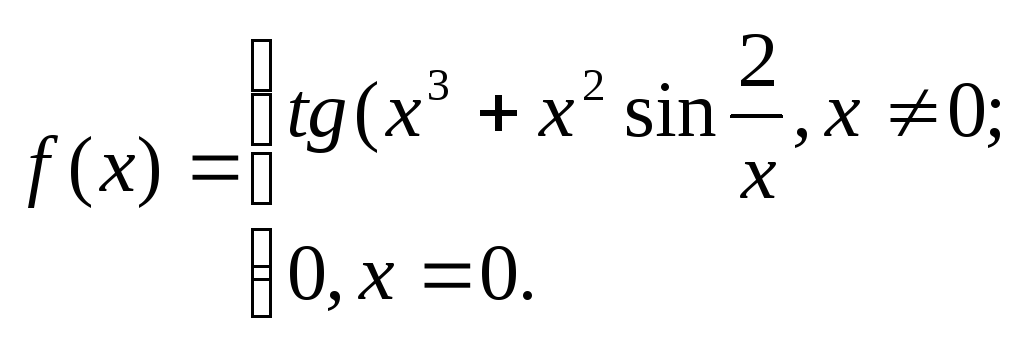 .
2.
.
2.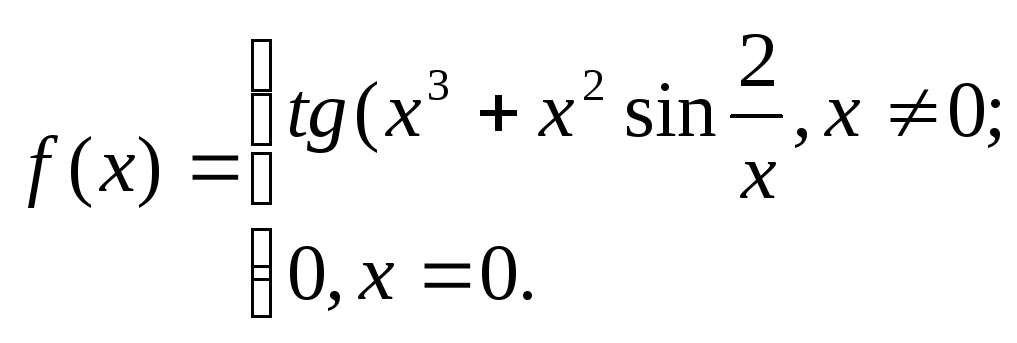 3.
3.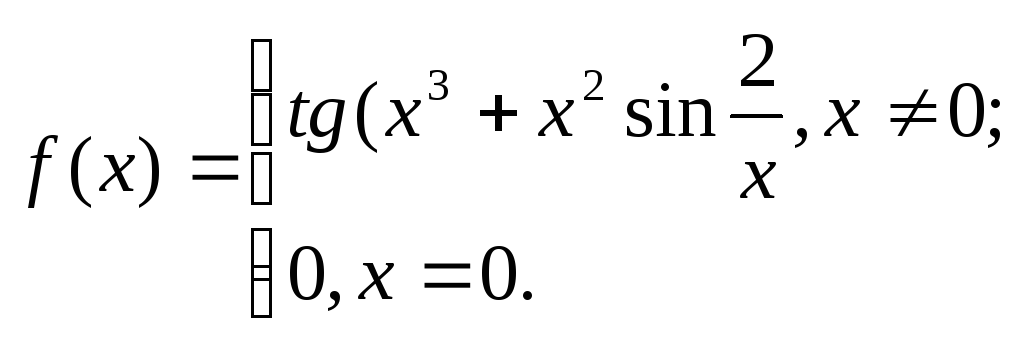 .
4.
.
4.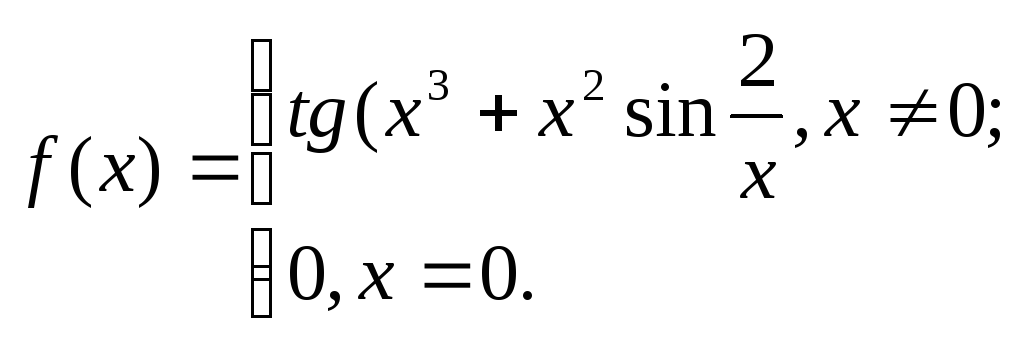 5.
5.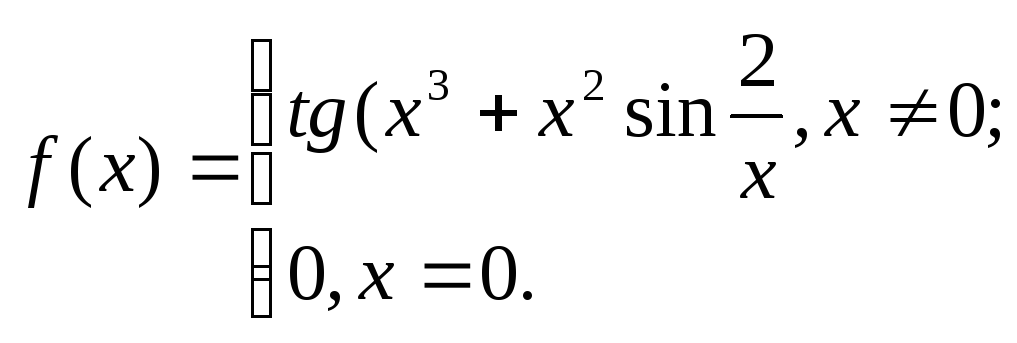
6.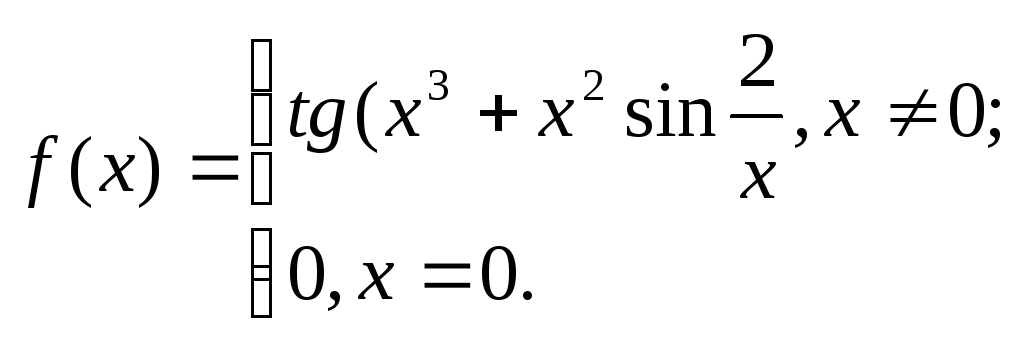 7.
7. 8.
8.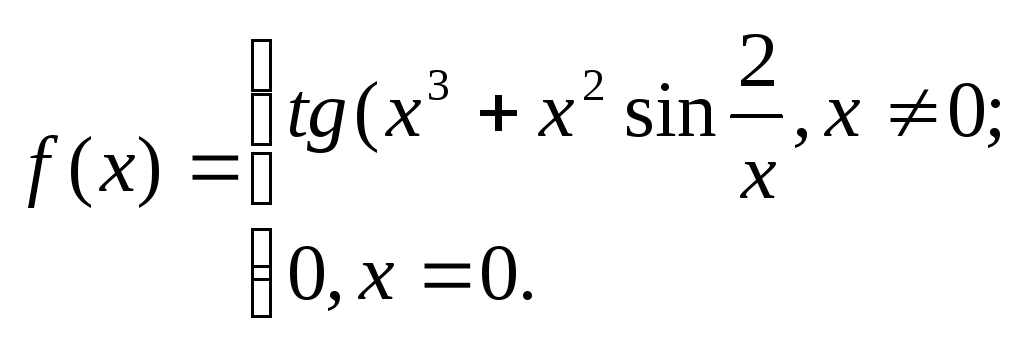 .
9.
.
9.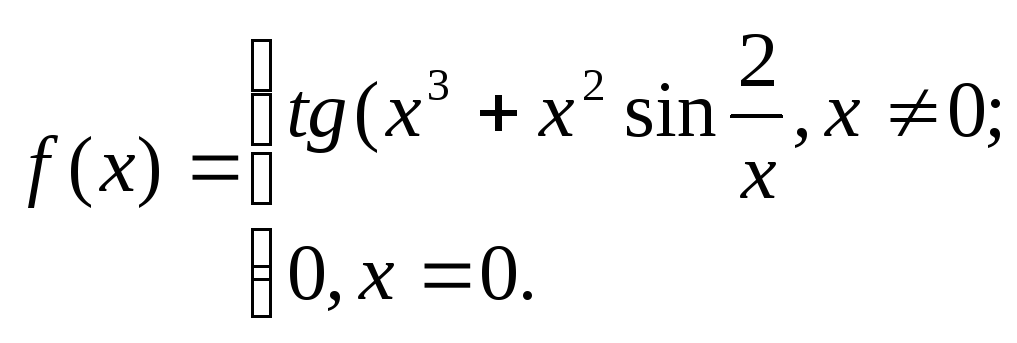 10.
10.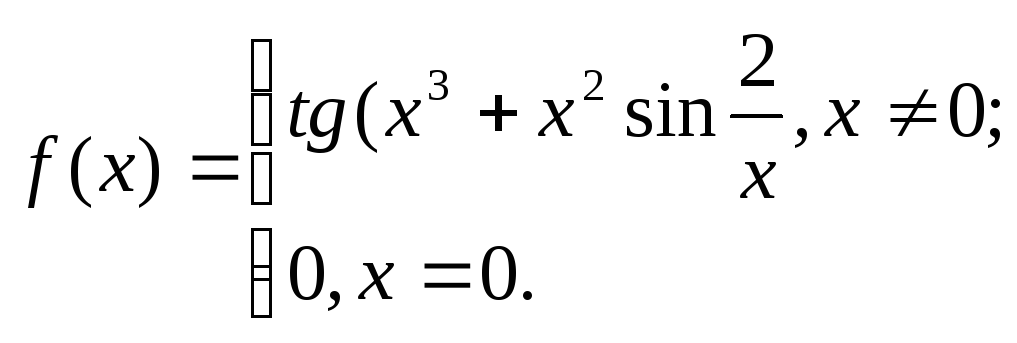
11.
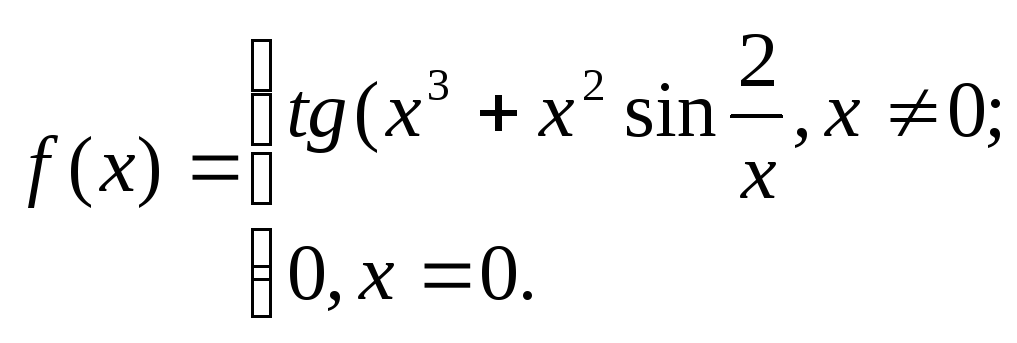 12.
12. 13.
13.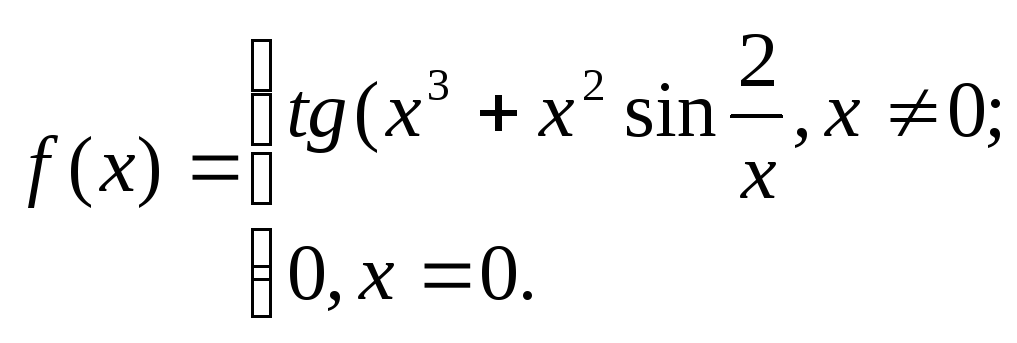 14.
14.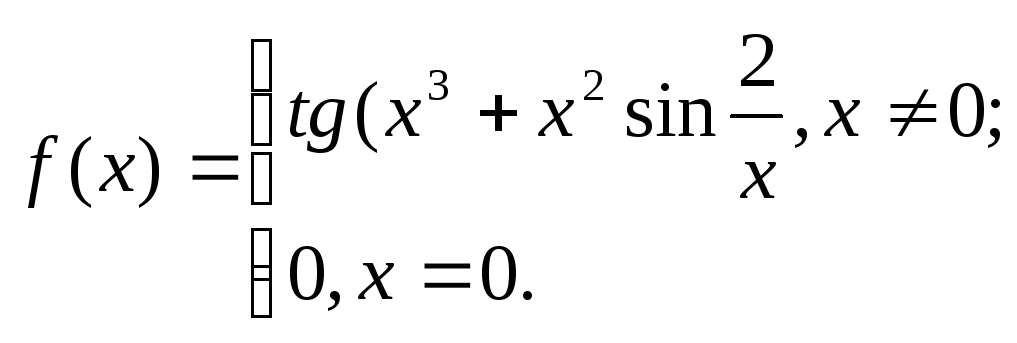 15.
15.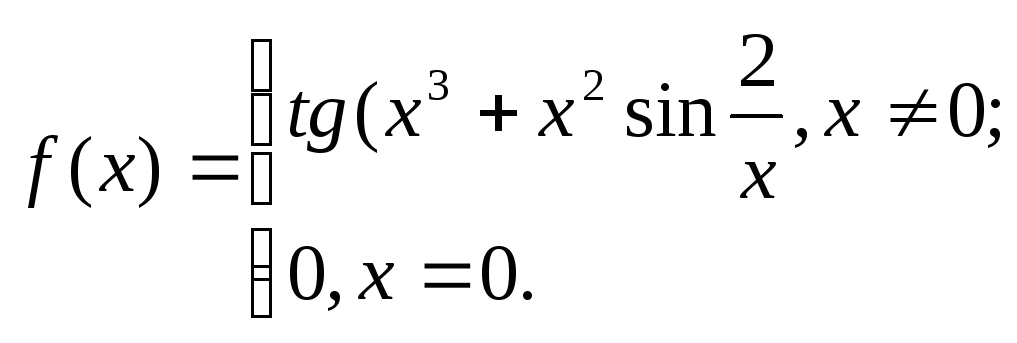 16.
16. 17.
17.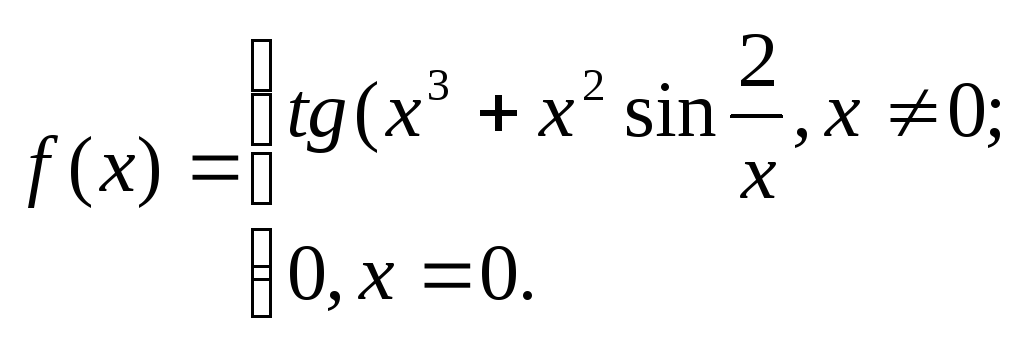 18.
18.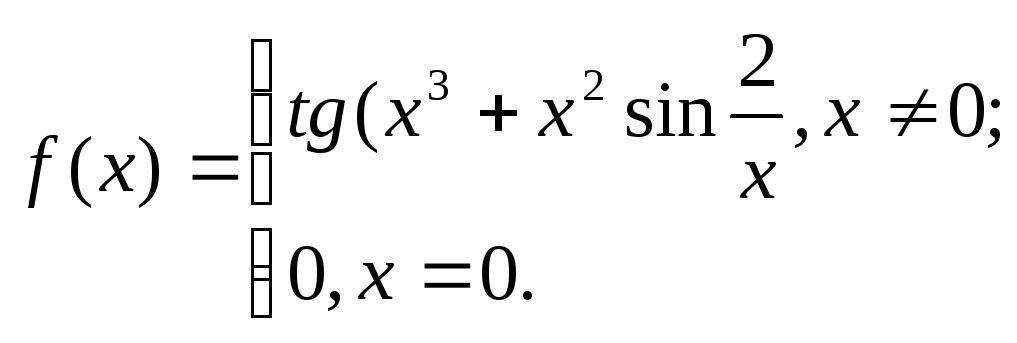 19.
19. 20.
20. 21.
21.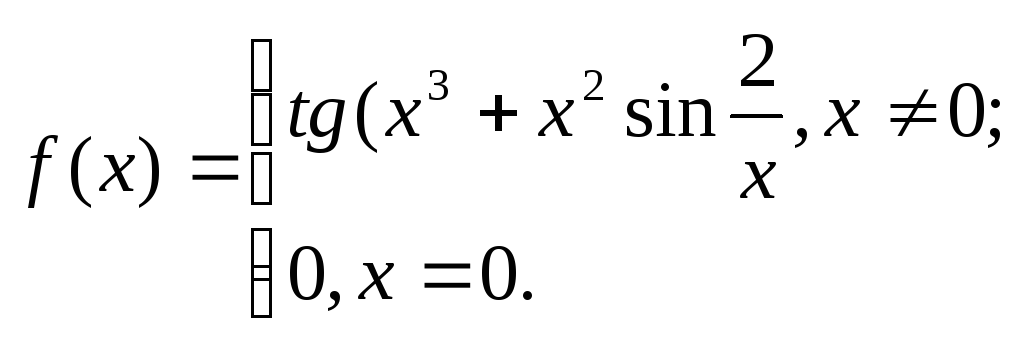
22.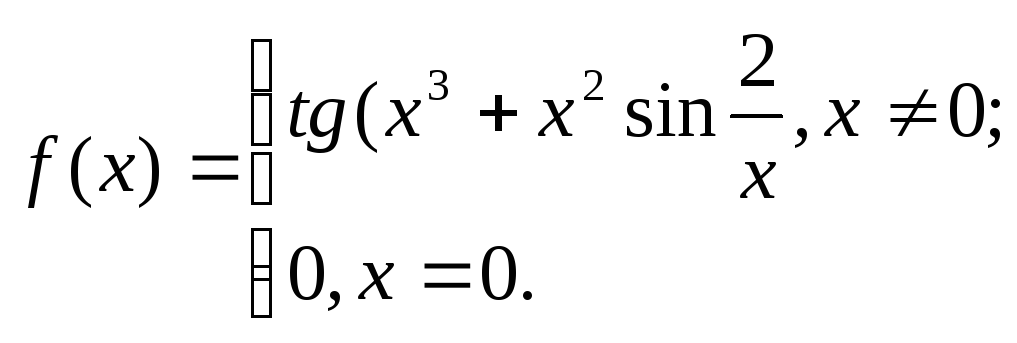 23.
23.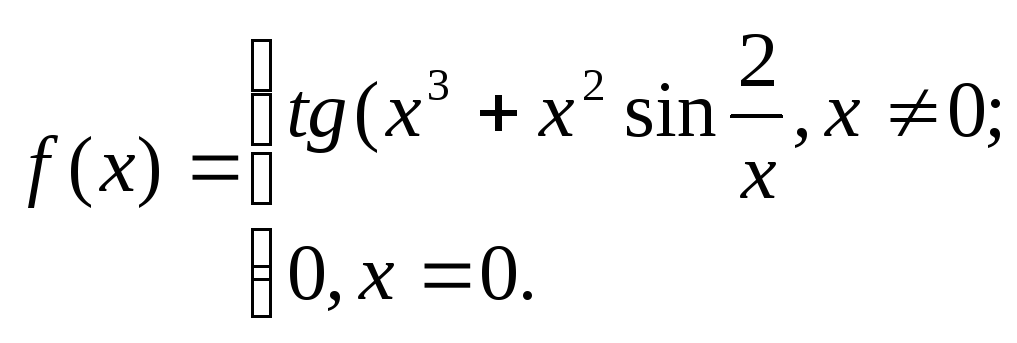 24.
24.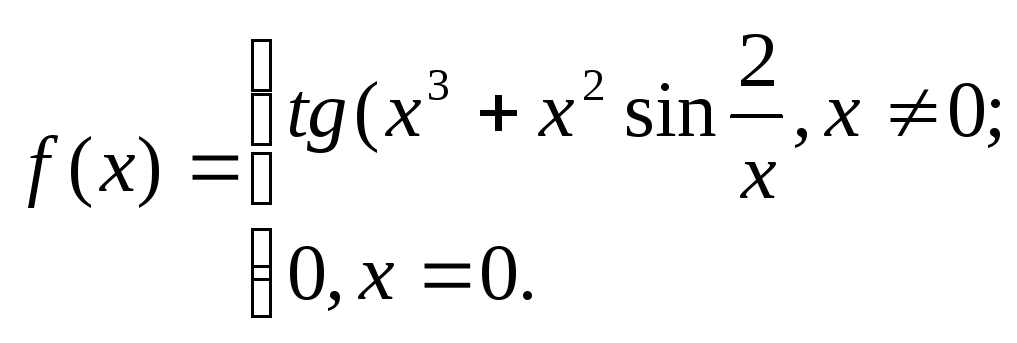 25.
25. 26.
26.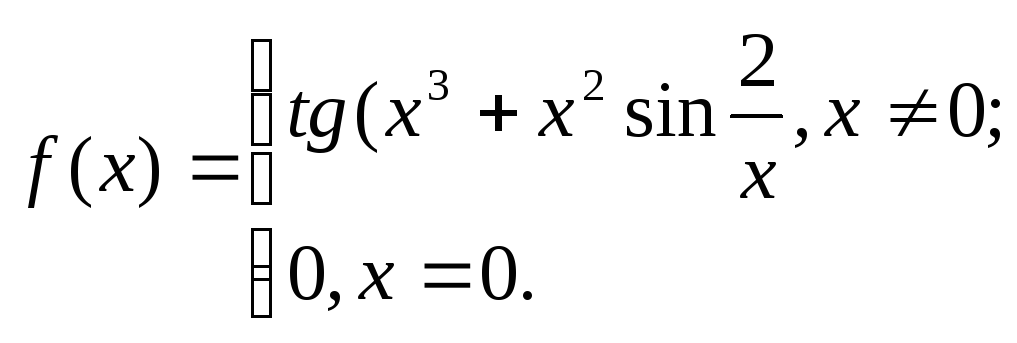 27.
27.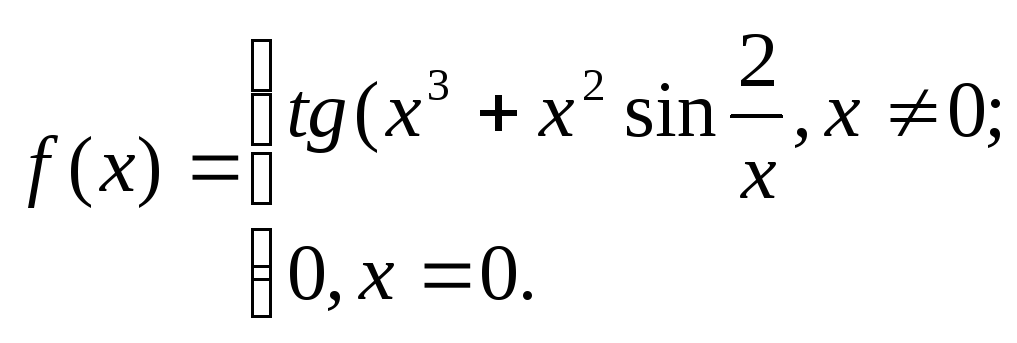 28.
28.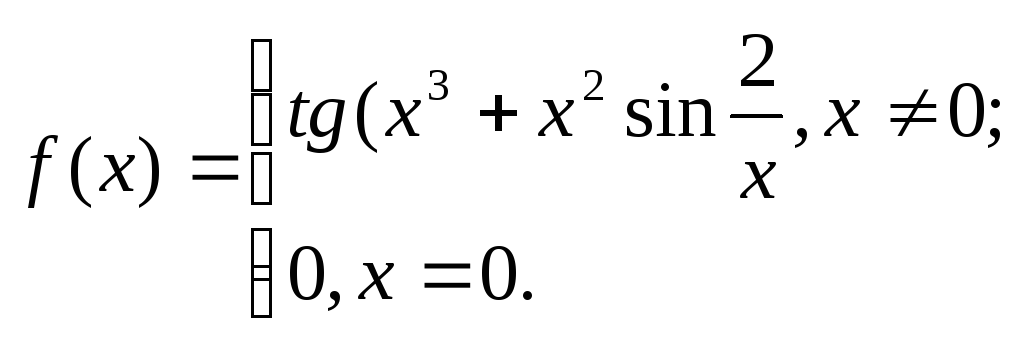 29.
29.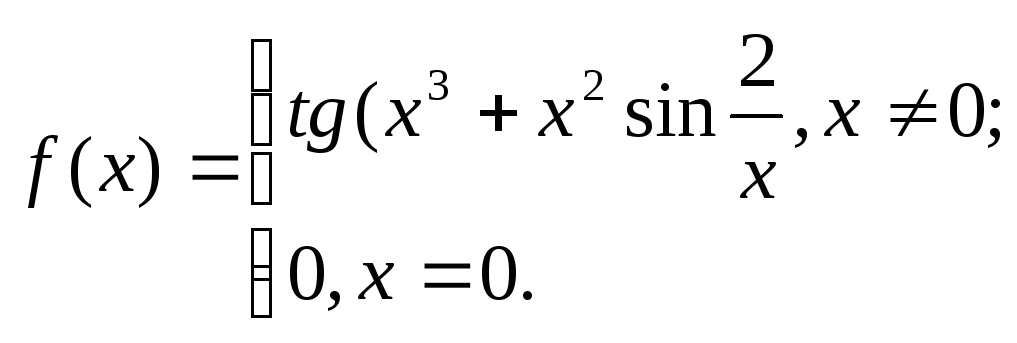 30.
30.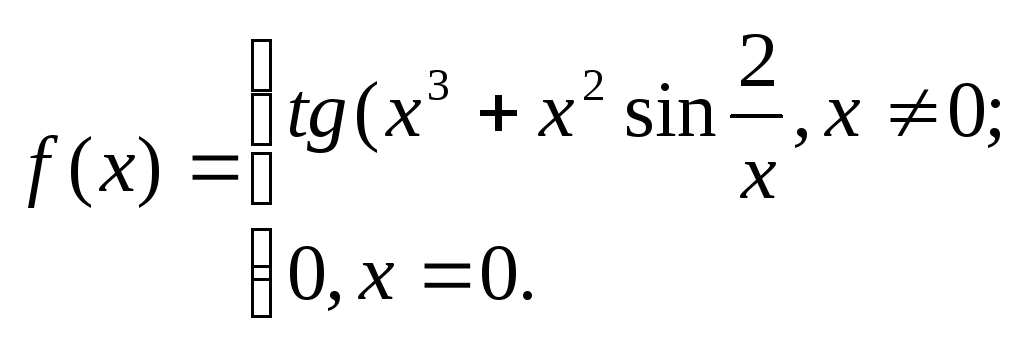 31.
31.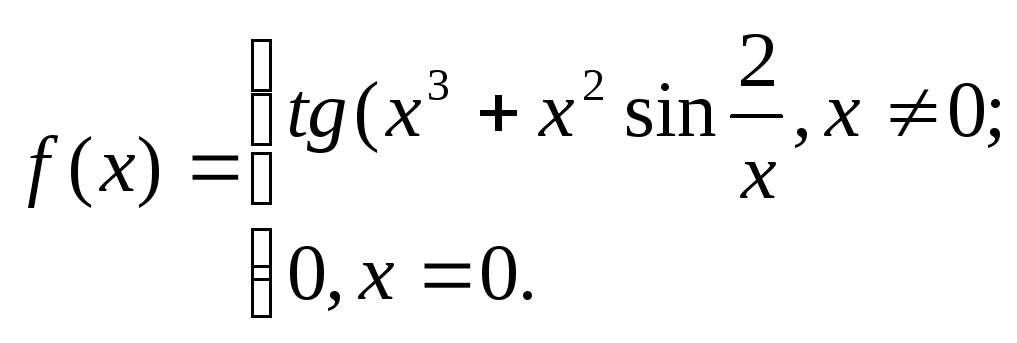
Задача
2. Составить
уравнение нормали (в вариантах 1-12) или
уравнение касательной (в вариантах
13-31) к данной кривой в точке с абсциссой
![]() .
.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
25.
![]() .
.
26.
![]() .
.
27.
![]() .
.
28.
![]() .
.
29.
![]() .
.
30.
![]() .
.
31.
![]() .
.
Задача
3. Найти
дифференциал
![]() .
.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]() 7.
7.![]() 8.
8.![]() 9.
9.![]() 10.
10.![]() 11.
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]() 17.
17.![]() 18.
18.![]() 19.
19.![]() 20.
20.![]()
21.![]() 22.
22.![]() 23.
23.![]() 24.
24.![]() 25.
25.![]() 26.
26.![]() 27.
27.![]() 28.
28.![]() 29.
29.![]() 30.
30.![]() 31.
31.![]()
Задача 4. Вычислить приближенно с помощью дифференциала.
1.![]() ,
,
![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.![]()
11.
![]()
12.
![]()
13.![]()
14.![]()
15.![]()
16.![]()
17.![]()
18.
![]()
19.![]()
20.![]()
21.![]()
22.![]()
23.![]()
24.
![]()
25.![]()
26.![]()
27.![]()
28.![]()
29.![]()
30.
![]()
31.![]()
Задача 5. Найти производную.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача 6. Найти производную.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача 7. Найти производную.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача 8. Найти производную.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача 9. Найти производную.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача 10. Найти производную.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
