
- •I. Первообразная и неопределенный интеграл
- •II. Методы интегрирования
- •2.1. Непосредственное интегрирование
- •2.2. Метод замены переменной (подстановки)
- •2.3. Метод интегрирования по частям
- •III. Интегрирование рациональных дробей
- •3.1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:
- •3.2. Правильные и неправильные рациональные дроби
- •3.3. Разложение правильной дроби
- •3.4. Нахождение коэффициентов
- •3.5. Правило интегрирования рациональных дробей
- •IV. Интегрирование некоторых иррациональностей
- •V. Интегрирование тригонометрических выражений
- •VI. Определенный и несобственный интегралы, их вычисление
- •VII. Геометрические приложения определенного интеграла
- •Из чертежа видно, что
I. Первообразная и неопределенный интеграл
Определение
1. Функция
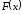 называется первообразной для
называется первообразной для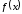 ,
если
,
если
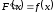 (1)
(1)
или
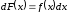 (2)
(2)
Пример
1.
 есть первообразная для
есть первообразная для ,
так как
,
так как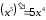 или
или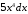 .
.
Пример
2.
 есть первообразная для
есть первообразная для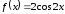 ,
так как
,
так как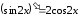 или
или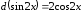 .
.
Всякая
непрерывная функция
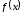 имеет бесчисленное первообразная,
которое отличаются друг друга на
постоянное число.
имеет бесчисленное первообразная,
которое отличаются друг друга на
постоянное число.
Так
в 1-м примере для
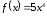 первообразный будут, кроме
первообразный будут, кроме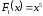 ,
,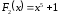 ,
,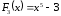 ,
,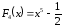 ,
и другие. Все они удовлетворяют условию
(1) и (2). Вообще в общем виде можно записать
первообразную в виде
,
и другие. Все они удовлетворяют условию
(1) и (2). Вообще в общем виде можно записать
первообразную в виде ,
где
,
где – произвольная постоянная. Действительно,
– произвольная постоянная. Действительно,
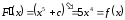
или
 .
.
Определение
2. Общее
выражение
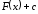 совокупности всех первообразных для
функции
совокупности всех первообразных для
функции называется неопределенным интегралом
от этой функции и обозначается
называется неопределенным интегралом
от этой функции и обозначается
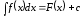 (3)
(3)
При
этом
 ,
где
,
где
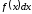 –подынтегральное
выражение,
–подынтегральное
выражение,
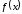 –подынтегральная
функция.
–подынтегральная
функция.
Операцию нахождения неопределенного интеграла называют интегрированием.
Итак, интегрирование представляет собой операцию, обратную дифференцированию, поэтому каждой формуле дифференцирования (1) соответствуют формула интегрирования (3).
Пример
3.
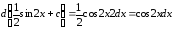
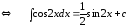 ,
,
где
 –const.
–const.
Ниже приведена таблица основных интегралов. Каждую формулу можно проверить дифференцированием.
Таблица основных интегралов
1.
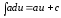 (
(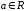 ,
, –const,
–const,
 )
)
2.
 (для
любого
(для
любого )
)
2.1.
 2.2.
2.2.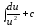
3.
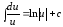
4.
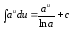 (
(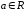 ,
,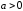 ,
, )
)
5.
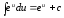
6.
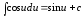
7.
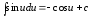
8.
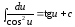
9.
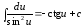
10.
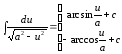 (
( )
)
11.
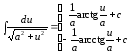 (
(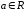 )
)
12.

13.
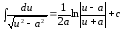
При интегрировании используются свойства интегралов.
Свойства интегралов
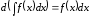
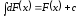 ,
в частности,
,
в частности,

 ,
, 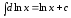
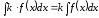 ,
где
,
где
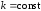
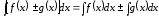
Таблицу интегралов и свойства необходимо выучить наизусть.
II. Методы интегрирования
Существуют три способа интегрирования: непосредственное, заменой переменной и по частям.
2.1. Непосредственное интегрирование
Непосредственное интегрирование состоит в том, что подынтегральную функцию путем тождественных преобразований с использованием формул алгебры и тригонометрии, а также используя свойства (3) и (4), сводят к табличным интегралам.
Рассмотрим несколько примеров.
Пример
4.
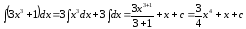 .
.
(использованы
свойства 3, 4; табличный интеграл 2,
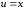 )
)
Правильность ответа проверяем дифференцированием:
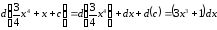 .
.
Пример
5.
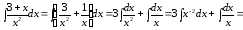
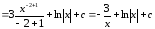 .
.
(свойства 3, 44 табличные интегралы 2.2 и 3).
Пример
6.

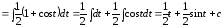
(свойства 3,4; табличные интегралы 1 и 7).
2.2. Метод замены переменной (подстановки)
Для
вычисления интеграла
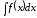 сделаем замену
сделаем замену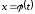 ,
где
,
где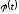 выбирается так, чтобы после преобразований
данного интеграла и новой переменной
выбирается так, чтобы после преобразований
данного интеграла и новой переменной ,
получился интеграл, который берется
непосредственно.
,
получился интеграл, который берется
непосредственно.
Предварительно
находим
 ,
тогда
,
тогда
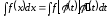 .
(4)
.
(4)
После
нахождения первообразной
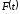 необходимо вернуться к первоначальной
переменной «
необходимо вернуться к первоначальной
переменной « ».
».
Пример
7.
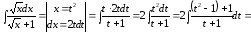
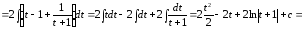
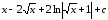 .
.
Пример
8.
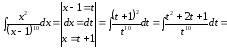

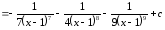 .
.
Замечание. Следующие интегралы удобно решать указанной заменой
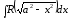 ,
,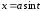 ;
;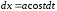 ;
;
 ,
,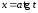 ;
;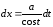 ;
;
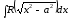 ,
,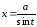 ;
; .
.
Пример
9.
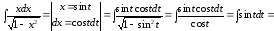
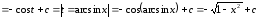 ,
,
т.
к.
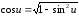 .
.
Формулой (4) часто пользуются справа налево:
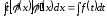 ,
,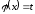 .
(5)
.
(5)
При
этой замене надо помнить, что в составе
подынтегрального выражения должен быть
дифференциал функции
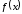 .
.
Такой метод называется под знак дифференциала
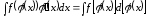 .
(5’)
.
(5’)
При использовании этого метода можно воспользоваться таблицей дифференциалов.
Таблица дифференциалов
1.
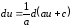 ,
, –const,
–const,
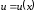 ,
,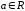
2.
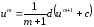

3.
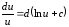
4.
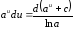 ,
,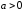 ,
,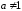 ,
,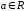
5.
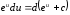
6.
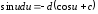
7.
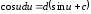
8.

9.
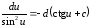
10.
 ,
,
11.
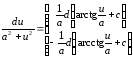 ,
,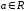
Пример
10.
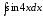
Согласно
таблице дифференциалов, 1, с. 7
 ,
положим
,
положим ,
, ,
, ,
,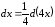 .
.
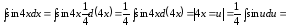
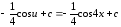 .
.
Пример
11.
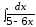
По
таблице дифференциалов, 1, с. 7
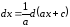 ,
положим
,
положим
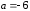 ,
,
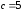 ,
,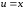 ,
,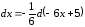 .
.
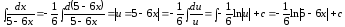 .
.
Пример
12.
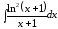 – можно найти двумя способами:
– можно найти двумя способами:
1
способ.
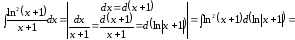
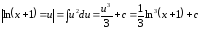 ;
;
2
способ.
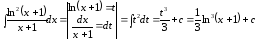 .
.
Пример
13.

1
способ.
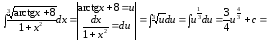
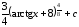 ;
;
2
способ.
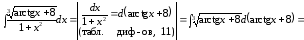
 .
.
Пример
14.
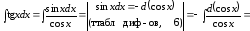
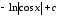 .
(табл. интегр., 3,
.
(табл. интегр., 3,
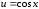 )
)
