Тема № 9. Остовые деревья минимального веса

Многие вещи нам непонятны не потому,

что наши понятия слабы; но потому,

что сии вещи не входят в круг наших понятий.

( Козьма Прудков )

9.1. Минимальные покрывающие деревья

Пусть даны n контактов на печатной плате, которые мы хотим электрически соединить. Для этого достаточно использовать n ‑1 проводов, каждый из которых соединяет два контакта. При этом мы обычно стремимся сделать суммарную длину проводов как можно меньше.

Упрощая ситуацию, можно сформулировать задачу так. Пусть имеется связный неориентированный граф G = (V, Е), в котором V — множество контактов, а E — множество их возможных попарных соединений. Для каждого ребра графа (u, v) задан вес w(u, v) (длина провода, необходимого для соединения u и v). Задача состоит в нахождении подмножества Т Е, связывающего все вершины, для которого суммарный вес

w(T) = w(u,v)

минимален. Такое подмножество Т будет деревом (поскольку не имеет циклов: в любом цикле один из проводов можно удалить, не нарушая связности). Связный подграф графа G, являющийся деревом и содержащий все его вершины, называют покрывающим деревом (spanning tree) этого графа. (Иногда используют термин "остовое дерево"; для краткости мы будем говорить просто "остов".)

Далее мы рассмотрим задачу о минимальном покрывающем дереве (minimum-spanning-tree problem). Здесь слово "минимальное" означает "имеющее минимально возможный вес.

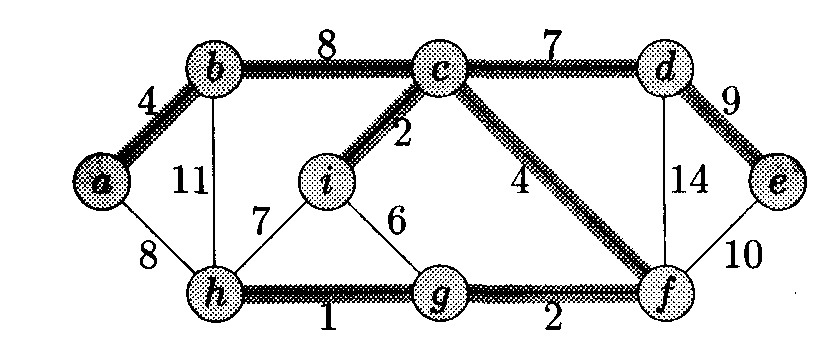
Рис 9.1. Минимальное покрывающее дерево.

На Рис 9.1 показано на примере минимальное покрывающее дерево. На каждом ребре графа указан вес. Выделены ребра минимального покрывающего дерева (суммарный вес 37). Такое дерево не единственно: заменяя ребро (b, с) ребром (а, h), получаем другое дерево того же веса 37.

Рассмотрим два способа решения задачи о минимальном покрывающем дереве: алгоритмы Крускала и Прима. Каждый их них легко реализовать со временем работы O(E log₂V), используя обычные двоичные кучи. Применив фибоначчиевы кучи, можно сократить время работы алгоритма Прима до O(E+V log₂V) (что меньше Е log₂V, если |V| много меньше |Е|).

Оба алгоритма следуют "жадной" стратегии: на каждом шаге выбирается "локально наилучший" вариант. Не для всех задач такой выбор приведёт к оптимальному решению, но для задачи о покрывающем дереве это так. Здесь будет описана общая схема алгоритма построения минимального остова (добавление рёбер одного за другим). В дальнейшем будут указаны две конкретных реализации общей схемы.

9.2. Построение минимального остова

Пусть дан связный неориентированный графа G = (V, Е) и весовая функцией w: Е .Будем искать минимальное покрывающее дерево (остов), следуя жадной стратегии.

Общая схема алгоритма будет такова. Искомый остов строится постепенно: к изначально пустому множеству А на каждом шаге добавляется одно ребро. Множество А всегда является подмножеством некоторого минимального остова. Ребро (u, v), добавляемое на очередном шаге, выбирается так, чтобы не нарушить этого свойства: А{(u, v)} тоже должно быть подмножеством минимального остова. Мы называем такое ребро безопасным ребром (safe edge) для А.

Generic-MST(G,w)

1 А

2 while A не является остовом

3 do найти безопасное ребро (u,v) для А

4 А A{(u,v)}

5 return A

Рис 9.2. Два изображения одного и того же разреза графа с Рис 9.1

(а) Вершины множества S изображены чёрными, его дополнения V\S — белым. Рёбра, пересекающие разрез, соединяют белые вершины с черными. Единственное лёгкое ребро, пересекающее разрез — ребро (d, с). Множество А состоит из серых ребер. Разрез (s, V \S) согласован с А (ни одно ребро из А не пересекает разрез).

(б) Вершины множества S изображены слева, вершины V \ S — справа. Ребро пересекает разрез, если оно пересекает вертикальную прямую.

По определению безопасного ребра свойство "А является подмножеством некоторого минимального остова" (для пустого множества это свойство, очевидно, выполнено) остаётся истинным для любого числа итераций цикла, так что в строке 5 алгоритм выдаёт минимальный остов. Конечно, главный вопрос в том, как искать безопасное ребро в строке 3. Такое ребро существует (если А является подмножеством минимального остова, то любое ребро этого остова, не входящее в А, является безопасным). Заметим, что множество А не может содержать циклов (поскольку является частью минимального остова). Поэтому добавляемое в строке 4 ребро соединяет различные компоненты графа G_a = (V,A), и с каждой итерацией цикла число компонент уменьшается на 1. Вначале каждая точка представляет собой отдельную компоненту; в конце весь остов — одна компонента, так что цикл повторяется |V| — 1 раз.

Приведем правило отыскания безопасных ребер (теорема 9.1). Начнём с определений. Разрезом (cut) (S,V \S) неориентированного графа G = (V, Е) называется разбиение множества его вершин на два подмножества (рис. 9.2). Говорят, что ребро (u, v) Е пересекает (crosses) разрез (S, V \ S), если один из его концов лежит в S, а другой — в V \S. Разрез согласован с множеством рёбер A (respects the set А), если ни одно ребро из А не пересекает этот разрез. Среди пересекающих разрез рёбер выделяют рёбра наименьшего веса (среди пересекающих этот разрез), называя их лёгкими (light edges).

Теорема 9.1. Пусть G = (V, Е) — связный неориентированный граф, на множестве вершин которого определена вещественная функция w. Пусть А — множество рёбер, являющееся подмножеством некоторого минимального остова графа G. Пусть (S, V \ S) — разрез графа G, согласованный с А, а (u, v) — лёгкое ребро для этого разреза. Тогда ребро (u, v) является безопасным для А.

Вершины S — чёрные, вершины V \S — белые. Изображены только рёбра минимального остова (назовём его Т). Рёбра множества А выделены серым цветом; (u, v) — лёгкое ребро, пересекающее разрез (S, V \ S); (х, у) — ребро единственного пути р от u к v в Т.

Доказательство:

Пусть Т — минимальный остов, содержащий А. Предположим, что Т не содержит ребра (u,v), поскольку в противном случае доказываемое утверждение очевидно. Покажем, что в этом случае существует другой минимальный остов Т’, содержащий ребро (u, v), так что это ребро является безопасным. Остов Т связный и потому содержит некоторый путь р из u в v (рис. 9.3).

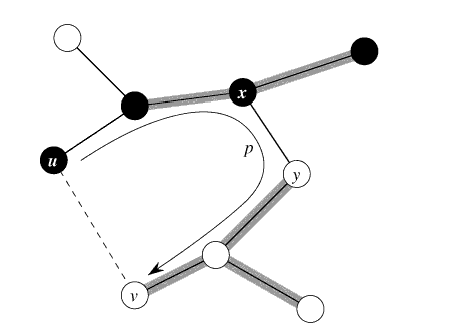
Рис 9.3. К доказательству теоремы

Поскольку вершины u и v принадлежат разным частям разреза (S, V \ S), в пути р есть по крайней мере одно ребро (x, у), пересекающее разрез. Это ребро не лежит в А, так как разрез согласован с А. Удаление из дерева Т ребра (x, у) разбивает его на две компоненты. Добавление (u,v) объединяет эти компоненты в новый остов

Т' = Т \ {(x, у)} U {(u, v)}. Покажем, что Т' — минимальный остов. Поскольку (u, v) — лёгкое ребро, пересекающее разрез (S, V \S), изъятое из Т ребро (x, у) имеет не меньший вес, чем добавленное вместо него ребро (u, v), так что вес остова мог только уменьшиться. Но остов был минимальным, значит, вес его остался прежним, и новый остов Т' будет другим минимальным остовом (того же веса). Поэтому ребро (u, v), содержащееся в Т', является безопасным.

Следующее следствие теоремы1 будет использовано далее.

Следствие. Пусть G = (V, Е) — связный неориентированный граф и на множестве Е определена вещественная функция w. Пусть А — множество рёбер графа, являющееся подмножеством некоторого минимального остова. Рассмотрим лес G_a = (V,A). Пусть дерево С — одна из связных компонент леса G_a. Рассмотрим все рёбра графа, соединяющие вершины из С с вершинами не из С, и возьмём среди них ребро наименьшего веса. Тогда это ребро безопасно для А. Очевидно: разрез (С, V \C) согласован с A, а ребро (u, v) — лёгкое ребро для этого разреза.

Доказательство. Очевидно: разрез (С,V \C) согласован сA, а ребро(u, v) — лёгкое ребро для этого разреза.