Теорема 8.4 Множество X является множеством баз матроида m тогда и только тогда, когда выполняются следующие два свойства:

1. Множество B непусто.

2. Если B₁, B₂  В, x  B₁ − B₂, тогда существует y  B₂ − B₁, такой, что (B₁ − x)  {y}  B.

Доказательство. Пусть выполняются два приведенных свойства. Необходимо доказать, что B содержит все базы. Опять проведем доказательство от противного. Пусть B₁  B. Но есть элемент l, такой что B₁  {l}  B, l = B₁ − B. Но тогда такого элемента Y  B − (B  {l}) не существует.

Пусть B — множество баз, докажем что имеют место оба свойства. Первое свойство — очевидно. Рассмотрим второе свойство. x  B₁ − B₂. Но не существует такого y  B₂ − B₁, что B₁ − x  {y}  B. Но это противоречит третьему свойству матроидов, так как |B₁ − {x}| + 1 = |B₂|, и такой y должен существовать.

Следствие. Мощность любой базы является одинаковой (по 2 свойству). Рангом матроида называется мощность его базы.

Теорема 8.5 Множество C является множеством простых циклов матроида тогда и только тогда, когда выполняются следующие три свойства:

1. Ни один из элементов C не является пустым множеством.

2. Ни один элемент C не является подмножеством другого элемента C.

3. Если C₁ и C₂  C и e  C₁ ∩ C₂, то (C₁  C₂) − e содержат какой-то элемент C.

Доказательство. Аналогично уже приведенным двум доказательствам. Читателю предлагается проделать его самостоятельно.

Матроиды имеют широкое применение в задачах, связанных с комбинаторной оптимизацией, а также с задачами, решение которых основано на жадных алгоритмах.

Рассмотрим такую задачу: у менеджера есть m однодневных работ для одного человека J₁, J₂, J₃, …, J_m. Также он располагает n рабочими, каждый из которых умеет выполнять какой-то поднабор работ. Менеджер хочет знать, какое максимальное количество работ способны выполнить его рабочие за один день. Как позже выяснится, это будет рангом некоего матроида.

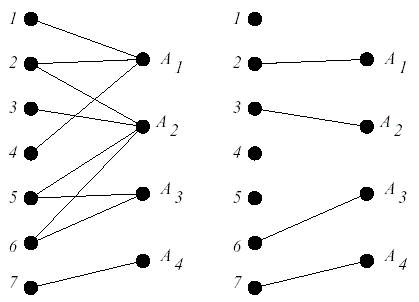
Пусть A — множество подмножеств некоего множества E. К примеру, пусть A=({1,2,4}, {2,3,5,6}, {5,6}, {7}), при множестве E={1, 2, 3, 4, 5, 6, 7}. Подмножество E — {x₁, x₂, …, x_k} называется частичным трансверсалем A, если есть взаимнооднозначное соответствие Φ между {1, 2, …, k} и {1, 2, …, m}, причем x_i  A_Φ(i) для любых i. Если m = k, то такой частичный трансверсаль называется трансверсалем. Если взять множество {2,3,6,7}, то оно будет трансверсалем для A, как это видно из рисунка слева.

Теорема 8.6 Пусть a — какое-то множество подмножеств e, а I — множество частичных трансверсалей множества a. Тогда пара e, I — матроид.

Доказательство. Каждое подмножество частичного трансверсаля — частичный трансверсаль. Пустое множество также частичный трансверсаль. Поэтому первые два свойства матроидов выполняются. Для доказательства третьего свойства матроидов построим двудольный граф. Он, а также максимальное паросочетание в нем изображены на рисунке. Пусть вершины слева будут соответствовать элементам множества E, а вершины справа — элементам множества A. Ребро из левой доли в правую есть тогда и только тогда, когда соответствующий элемент левой доли принадлежит соответствующему элементу правой доли. Частичный трансверсаль соответствует паросочетанию в графе. Пусть X и Y будут частичными трансверсалями и |X| = |Y| + 1. Раскрасим ребра из паросочетания, соответствующего X в синий цвет, а соответствующего Y — в красный. Причем ребра, соответствующие двум паросочетаниям, будут окрашены в пурпурный цвет. Таким образом, получится |X − Y| ребер синего цвета, |Y − X| ребер красного цвета, и будет выполняться соотношение |X − Y| = |Y − X| + 1. Рассмотрим подграф H, индуцированный красными и синими ребрами из исходного графа. Каждая вершина соответствует либо двум ребрам — синему и красному, либо одному — синему или красному. Понятно, что любая компонента связности представляет собой либо путь, либо цикл, состоящий из чередующихся красных и синих ребер. Так как граф двудольный, любой цикл состоит из четного числа ребер. Так как синих ребер на одно больше, чем красных, то должен существовать путь, начинающийся и оканчивающийся синим ребром. Обозначим этот путь H′. Поменяем в H′ синий и красный цвета. Получаем, что ребра, окрашенные в красный и пурпурный цвета образуют паросочетание в графе. Дальше легко показать, что подмножество E соответствующее этому новому паросочетанию имеет вид Y  {x}, где x — это некоторый элемент из X − Y.

Возвращаясь к задаче, поставленной в начале раздела. Понятно, что ранг матроида из частичных трансверсалей будет соответствовать мощности максимального паросочетания в двудольном графе, которое в свою очередь равно максимальному количеству работ, которых рабочие смогут выполнить за один день.

Взвешенный матроид — матроид, на элементах множества E задана положительная весовая функция w.

А теперь сам алгоритм: B_G = Ø. Пока существует e  B_G, такой что B_G  {e}  I и w(e) — максимально, B_G := B_G  {e}.