Кодирование информации

Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для

каждой буквы соответствующую ей кодовую комбинацию:
zl	z2	z3	z4	z5	z6	z7	z8
01	00	111	110	100	1011	10101	10100

1.5. Префиксные коды

Рассмотрев методики построения эффективных кодов, нетрудно убедиться в том, что эффект достигается благодаря присвоению более коротких кодовых комбинаций более вероятным буквам и более длинных – менее вероятным буквам. Таким образом, эффект связан с различием в числе символов кодовых комбинаций. А это приводит к трудностям при декодировании. Конечно, для различения кодовых комбинаций можно ставить специальный разделительный символ, но при этом значительно снижается желаемый эффект, так как средняя длина кодовой комбинации по существу увеличивается на символ.

Более целесообразно обеспечить однозначное декодирование без введения дополнительных символов. Для этого эффективный код необходимо строить так, чтобы ни одна комбинация кода не совпадала с началом более длинной комбинации. Коды, удовлетворяющие этому условию, называются префиксными кодами. Последовательность комбинаций префиксного кода, например, кода

	z1		z2		z3	z4
	00		01		101	100
декодируется однозначно:
100	00	01	101		101	101	00
z4	z1	z2		z3	z3	z3	z1
Последовательность комбинаций непрефиксного кода, например кода
	z1	z2			z3	z4
	00	01		101		010

(комбинация 01 является началом комбинации 010), может быть декодирована

по-разному:
00	01	01	01	010	101
z1	z2	z2	z2	z4	z3,
00	010	101		010	101
z1	z4		z3	z4	z3
или
00	01	010	101	01	01
z1	z2	z4	z3	z2	z2.

Нетрудно убедиться, что коды, получаемые в результате применения методики Шеннона – Фэно или Хаффмена, являются префиксными.

8

1.6. Упражнения и задачи

Задача 1.1

1. Построить оптимальный неравномерный код методом Хаффмана.

2. Построить оптимальный неравномерный код методом Шеннона – Фено.

Данные: Ра1=0,22, Ра2=0,58, Ра3=0,01, Ра4=0,03, Ра5=0,16.

Задача 1.2

Построить оптимальный неравномерный код методом Шеннона – Фено.

Данные: Ра1=1/8, Ра2=1/8, Ра3=1/8, Ра4=1/8, Ра5=1/4, Ра6=1/4.

Задача 1.3

Построить оптимальный код сообщения, состоящего из восьми равновероятных букв.

Задача 1.4

Построить оптимальный код передачи сообщения, в котором вероятность

	появления подчиняются закону		pi = 2−n , но ∑pi			=1.
		Варианты заданий
	Вариант		Вероятности
						Р(z3)=0,2
	1	Р(z1)=0,32	Р(z2)=0,26				Р(z4)=0,12
		Р(z5)=0,06	Р(z6)=0,02			Р(z7)=0,015	Р(z8)=0,005
						Р(z3)=0,15
	2	Р(z1)=0,38	Р(z2)=0,32				Р(z4)=0,1
		Р(z5)=0,03	Р(z6)=0,02
						Р(z3)=0,18
	3	Р(z1)=0,37	Р(z2)=0,25				Р(z4)=0,1
		Р(z5)=0,06	Р(z6)=0,04
						Р(z3)=0,18
	4	Р(z1)=0,26	Р(z2)=0,21				Р(z4)=0,11
		Р(z5)=0,1	Р(z6)=0,08			Р(z7)=0,06
						Р(z3)=0,16
	5	Р(z1)=0,24	Р(z2)=0,22				Р(z4)=0,16
		Р(z5)=0,12	Р(z6)=0,08			Р(z7)=0,02

9

РАЗДЕЛ 2. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ

2.1. Общая характеристика помехоустойчивых кодов

Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Шенноном и сформулированных им в виде основной теоремы для дискретного канала с шумом: при любой скорости передачи двоичных символов меньшей, чем пропускная способность канала, существует такой код, при котором вероятность ошибочного декодирования будет сколь угодно мала; вероятность ошибки не может быть сделана произвольно малой, если скорость передачи больше пропускной способности канала.

Как видно, в теореме не затрагивается вопрос о путях построения кода, обеспечивающего указанную идеальную передачу. Тем не менее, значение ее огромно, поскольку, обосновав принципиальную возможность такого кодирования, она мобилизовала усилия ученых на разработку конкретных кодов.

Кодирование должно осуществляться так, чтобы сигнал, соответствующий принятой последовательности символов, после воздействия на него предполагаемой в канале помехи оставался ближе к сигналу, соответствующему конкретной переданной последовательности символов, чем к сигналам, соответствующим другим возможным последовательностям (степень близости обычно определяется по числу разрядов, в которых последовательности отличаются друг от друга).

Это достигается ценой введения при кодировании избыточности, которая позволяет так выбрать передаваемые последовательности символов, чтобы они удовлетворяли дополнительным условиям, проверка которых на приемной стороне дает возможность обнаружить и исправить ошибки.

Коды, обладающие таким свойством, получили название помехоустойчивых. Они используются как для исправления ошибок (корректирующие коды), так и для их обнаружения.

У подавляющего большинства существующих в настоящее время помехоустойчивых кодов указанные выше условия являются следствием их алгебраической структуры. В связи с этим их называют алгебраическими кодами.

Алгебраические коды можно подразделить на два больших класса: блоковые и непрерывные.

В случае блоковых кодов процедура кодирования заключается в сопоставлении каждой букве сообщения (или последовательности из k символов, соответствующей этой букве) блока из n символов, причем в операциях по преобразованию принимают участие только указанные k символов и выходная последовательность не зависит от других символов в передаваемом сообщении.

Блоковый код называется равномерным, если n остается постоянным для всех букв сообщения.

10

Различают разделимые и неразделимые блоковые коды. При кодировании разделимыми кодами выходные последовательности состоят из символов, роль которых может быть отчетливо разграничена. Это информационные символы, совпадающие с символами последовательности, поступающей на вход кодера канала, и избыточные (проверочные) символы, вводимые в исходную последовательность кодером канала и служащие для обнаружения и исправления ошибок.

При кодировании неразделимыми кодами разделить символы выходной последовательности на информационные и проверочные невозможно.

Непрерывными называются такие коды, в которых введение избыточных символов в кодируемую последовательность информационных символов осуществляется непрерывно, без разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.

2.2.Кодовое расстояние

икорректирующая способность кода

При взаимно независимых ошибках наиболее вероятен переход в кодовую комбинацию, отличающуюся от данной в наименьшем числе символов.

Степень различия любых двух кодовых комбинаций характеризуется расстоянием между ними (по Хэммингу), или просто кодовым расстоянием. Оно выражается числом символов, в которых комбинации отличаются одна от другой, и обозначается через d.

Чтобы рассчитать кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2. Например заданы две кодовые комбинации А и В. Требуется определить кодовое расстояние. Складывая по модулю 2 А и В, получаем некоторую комбинацию С. Непосредственный подсчет единиц определяет вес ϖ(С) кодовой комбинации С, который равен кодовому расстоянию d.

А 1 0 0 1 1 1 1 1 0 1		ϖ(А)=7
В	1 1 0 0 0 0 1 0 1 0	ϖ(В)=4
С	0 1 0 1 1 1 0 1 1 1	ϖ(С)=7, d=7.

Минимальное расстояние, взятое по всем парам кодовых комбинаций данного кода, называется минимальным кодовым расстоянием.

Декодирование после приема может производиться таким образом, что принятая кодовая комбинация отождествляется с той разрешенной, которая отличается от полученной в наименьшем числе символов.

Такое декодирование называется декодированием по методу

максимального правдоподобия.

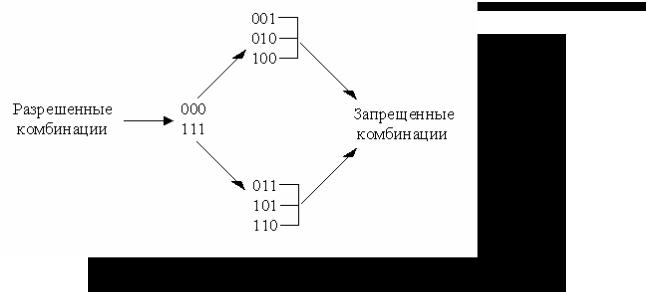
Очевидно, что при d=l все кодовые комбинации являются разрешенными. Например, при n=3 разрешенные комбинации образуют следующее множество:

000, 001, 010, 011, 100, 101, 110, 111.

11

Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Это случай равнодоступного кода, не обладающего способностью обнаруживать и исправлять ошибки.

Если d=2, то ни одна из разрешенных кодовых комбинаций при одиночной ошибке не переходит в другую разрешенную комбинацию. Например, подмножество разрешенных кодовых комбинаций может быть образовано по принципу четности в них числа единиц, как это приведено ниже для n=3:

000, 011, 101, 110

разрешенные комбинации

001, 010, 100, 111

запрещенные комбинации

Код обнаруживает все одиночные ошибки. В общем случае при необходимости обнаруживать ошибки кратности r минимальное хэммингово расстояние между разрешенными кодовыми комбинациями должно быть по крайней мере на единицу больше r, т. е,

d0min ≥r +1.

(2.1)

Действительно, в этом случае никакая r-кратная ошибка не в состоянии перевести одну разрешенную кодовую комбинацию в другую.

Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстояние между разрешенными кодовыми комбинациями должно быть не менее трех. При n=3 за разрешенные комбинации можно, например, принять 000 или 111. Тогда разрешенной комбинации 000 необходимо поставить в соответствие подмножество запрещенных кодовых комбинаций

001, 010, 100,

образующихся в результате возникновения единичной ошибки в комбинации

000.

Подобным же образом разрешенной комбинации 111 необходимо поставить в соответствие подмножество запрещенных кодовых комбинаций

110, 011, 101,

образующихся в результате возникновения единичной ошибки в комбинации

111:

12

Для возможности исправления ошибок кратности s и менее кодовое расстояние должно удовлетворять соотношению

dиmin ≥2s+1.

(2.2)

Нетрудно убедиться в том, что для исправления всех ошибок кратности s и менее и одновременного обнаружения всех ошибок кратности r (r≥s) и менее минимальное хеммингово расстояние нужно выбирать из условия

dи.о. min ≥r+s+1.

(2.3)

Каждый конкретный корректирующий код не гарантирует исправления любой комбинации ошибок. Коды предназначены для исправления комбинаций ошибок, наиболее вероятных для заданного канала.

Если характер и уровень помехи будут отличаться от предполагаемых, эффективность применения кода резко снизится. Применение корректирующего кода не может гарантировать безошибочность приема, но дает возможность повысить вероятность получения на выходе правильного результата.

2.3. Линейные групповые коды

Линейные коды всегда можно представить в систематической форме. Систематическими называют такие коды, в которых информационные и

корректирующие символы расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях. Они являются равномерными кодами, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину.

Систематические коды отличаются от сверточных тем, что в них формирование проверочных элементов происходит по nи информационным элементам кодовой комбинации. В канал связи идет n-элементная комбинация, состоящая из nи информационных и n–nи проверочных разрядов, тогда как в сверточных кодах проверочные элементы формируются путем сложения двух

13

или нескольких информационных элементов, сдвинутых друг от друга на расстояние, равное шагу сложения. Кроме того, в систематических кодах проверочные символы могут образовываться путем различных линейных комбинаций информационных символов. Декодирование систематических кодов также основано на проверке линейных соотношений между символами, стоящими на определенных проверочных позициях. В случае двоичных кодов этот процесс сводится к проверке на четность. Если число единиц четное, то линейная комбинация символов дает нуль, в противном случае – единицу.

Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.

Для двоичных кодов в качестве линейной операции используют сложение по модулю 2. Напомним его.

Правила сложения по модулю 2:

0 0 = 0; 0 1 = 1; 1 0 = 1; 1 1 = 0.

Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.

Свойство линейных кодов: сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий данному коду.

Линейные коды образуют алгебраическую группу 1 по отношению к операции сложения по модулю 2. В этом смысле они являются групповыми кодами2.

Свойство групповых кодов: минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.

Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонентов.

Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2.

Например, кодовое расстояние между двоичными векторами: 1100011 и 1001111 равно

1 1 0 0 0 1 1

1 0 0 1 1 1 1

0 1 0 1 1 0 0

d = 3.

Таким образом, Wмин = d.

2 Группа G – это некоторое множество G, где каждой паре элементов a, b сопоставлен некоторый однозначно определенный элемент c (также принадлежащий данному множеству), называемый произведением элементов a и b. При этом (ab)c = a(bc)

14

2.4. Код Хэмминга: идея построения

Код Хэмминга представляет собой один из важнейших классов линейных кодов, нашедших широкое применение на практике и имеющих простой и удобный для технической реализации алгоритм обнаружения и исправления одиночной ошибки.

Предположим, необходимо исправить одиночную ошибку бинарного кода. Такой код состоит из nи символов, несущих информацию, и nк контрольных (избыточных) символов. Всего символов в коде

n =nи +nк

(2.4)

При передаче кода может быть искажен любой информационный символ. Однако может быть и такой вариант, что ни один из символов не будет искажен, т. е. если всего n символов, то с помощью контрольных символов, входящих в это число, должно быть создано такое число комбинаций 2nк , чтобы свободно различить n+1 вариант.

Поэтому nк должно удовлетворять неравенству

2nк	≥ n+1.	(2.5)
Тогда, согласно (2.4)	= 2nк +nи = 2nк 2nи .
2n		(2.6)
Используя (2.5), запишем	≥ (n+1) 2nи ,
2n		(2.7)

где 2n – полное число комбинаций кода.

Отсюда число информационных символов кода, обнаруживающего и корректирующего одиночную ошибку,

2	n		≤	2n
		и			.	(2.8)
				(n +1)

Для вычисления основных параметров кода Хэмминга задается количество

либо информационных символов, либо информационных комбинаций N = 2nи . При помощи формул вычисляют n и nк. Соотношения между n, nи и nк для кода Хэмминга представлены в табл. 2.1.

Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие – контрольными. Практика показала, что номера контрольных символов удобно выбирать по закону 2i, где i = 0, 1, 2, 3, ... – натуральный ряд чисел. Номера контрольных символов в этом случае равны 1, 2, 4, 16, 32... Затем определяют значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом: сумма единиц на проверочных позициях должна быть четной. Если эта сумма четна – значение контрольного коэффициента нуль, в противном случае – единица.

15

Табл. 2.1 Соотношения между количеством информационных

и контрольных символов в коде Хэмминга

	n	nи	nк
	1	0	1
	2	0	2
	3	1	2
	4	1	3
	5	2	3
	6	3	3
	7	4	3
	8	4	4

	n		nи	nк
	9	5		4
	10	6		4
	11	7		4
	12	8		4
	13	9		4
	14	10		4
	15	11		4
	16	11		5

Проверочные позиции выбирают следующим образом. Составляют табличку для ряда натуральных чисел в двоичном коде. Число ее строк n =nк+nи Первой строке соответствует проверочный коэффициент a1, второй а2 и т. д.:

0001a1

0010а2

0011а3

0100а4

0101а5

0110а6

0111а7

1000a8

1001a9

1010а10

1011a11

Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые

содержат единицу в младшем разряде (а1, а3, а5, а7, а9, а11 и т. д.); во вторую – во втором разряде (а2, а3, а6, а7, a10, a11 и т. д.); в третью – в третьем разряде и т. д. Номера проверочных коэффициентов соответствуют номерам проверочных

позиций, что позволяет составить общую таблицу проверок (табл. 2.2).

16

Табл. 2.2

				Номера проверочных позиций кода Хэмминга
	№																										№ контроль-
	про-									Проверочные позиции (П)
																											ного символа
	верки
	1	1,	3,	5,	7,	9,		11,		...																	1
	2	2,	3,	6,	7,	10,		11,		14,		15,		18,		19,		22,		24, ...							2
	3	4,	5,	6,	7,	12,		13,		14,		15,		20,		21,		22,		23, ...							4
	4	8,	9,	10,	11,		12,		13,		14,		15,		24,		25,		26,		27,	28,	29,	30,	31,	40,	8
		41,	42, ...

Построение кода Хэмминга

Пример 2.1. Построить макет кода Хэмминга и определить значения корректирующих разрядов для кодовой комбинации (nи=4) 0101.

			Табл. 2.3
	Позиция	Кодовое слово
	символов	без значений	со значениями
	корректиру-	контрольных	контрольных
	ющего кода	коэффициентов	коэффициентов
	1	К1	0
	2	К2	1
	3	0	0
	4	К3	0
	5	1	1
	6	0	0
	7	1	1

Решение: Согласно табл. 2.1 минимальное число контрольных символов nк = 3, при этом n = 7. Контрольный коэффициенты будут расположены на позициях 1, 2, 4. Составим макет корректирующего кода и запишем его во вторую колонку табл. 2.3. Пользуясь табл. 2.2, определим значения

коэффициентов К1, К2 и К3.

Первая проверка: сумма П1+П3+П5+П7 должна быть четной, а сумма К1+0+1+1 будет четной при К1 = 0.

Вторая проверка: сумма П2+П3+П6+П7 должна быть четной, а сумма К2+0+0+1 будет четной при К2 = 1.

Третья проверка: сумма П4+П5+П6+П7 должна быть четной, а сумма К3+1+0+1 будет четной при К3 = 0.

Окончательное значение искомой комбинации корректирующего кода записываем в третью колонку табл. 2.3.

17