УЧЕБНИКИ 4 Экономика / Учебники по различным дисциплинам / Васильев Д.К. и др. Типовые решения в управлении проектами. 2003

Задача синтеза оптимального (e = 0) управления ОС заключа- ется в поиске допустимого управления, максимизирующего эффек- тивность для заданной ОС или ее модели (различий между ними пока мы не делаем):

(2) K(m) = sup K(u, m).

u U

То есть «классическому» принципу оптимальности K(m) соот- ветствует множество решений R0(m).

Будем считать, что U – метрическое пространство с метрикой ν, которая порождает метрику Хаусдорфа Hn(B1, B2), определяю- щую «расстояние» между подмножествами B1 и B2 множества U1.

Принцип оптимальности Rε(m) устойчив на модели m~ Î M

[32], если

(3) " a ³ 0 $ b ³ 0: " m Î M:

m(m, m~ ) £ b ® Hn(Rε( m~ ), Rε(m)) £ a.

Определение устойчивости (3) близко к определению устой- чивости по Ляпунову и качественно означает, что малые возмуще-

ния модели приводят к малым изменениям множеств оптимальных решений.

Критериальный принцип оптимальности R0(m) называется ус- тойчивым на модели m~ Î M, если функция K(m), определяемая (2), непрерывна на модели m~ . Более общие определения устойчи- вости принципов оптимальности можно найти, например, в [32].

Отметим, что когда речь идет об устойчивости принципа оп- тимальности, в (3) используется «расстояние» между множествами оптимальных решений (1). В то же время, если результаты модели- рования используются на практике, то для внедрения предлагается, как правило, единственное решение, поэтому введем определение устойчивости отдельного решения, удовлетворяющего тому или иному принципу оптимальности. Для критериального принципа оптимальности устойчивость решения u Î U на модели m~ опреде- ляется как непрерывность функции K(u, m) на модели m~ .

1 Особо следует отметить, что выбор метрик μ и ν должен в каждой конкретной задаче отражать прикладные потребности и соответство- вать содержательным интерпретациям.

11

Конкретное решение u Î U абсолютно устойчиво в области

B(e, u) Í M, если

(4) " m Î B(e, u) u Î Rε(m).

Другими словами, область абсолютной устойчивости (точнее – абсолютной ε-устойчивости) можно определить следующим обра-

зом: B(e, u) = {m Î M | u Î Rε(m)}.

Качественно абсолютная устойчивость конкретного решения u Î U в некоторой области означает, что оно ε-оптимально для любой ОС (и модели) из этой области. Понятно, что " u Î U,

" e1 ³ e2 ³ 0 B(0, u) Í B(e2, u) Í B(e1, u), то есть с ростом ε область абсолютной устойчивости конкретного решения не сужается.

Конкретные результаты анализа устойчивости решений ряда задач управления ОС приведены в [37].

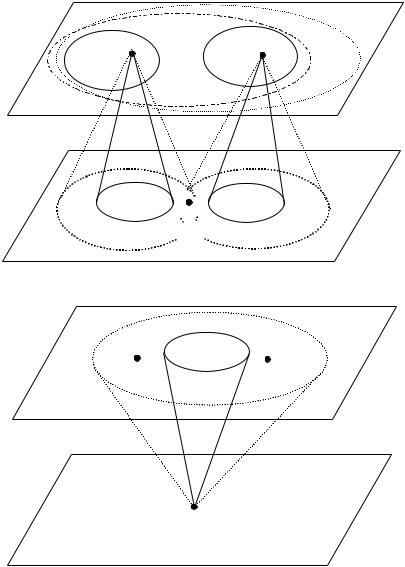
Таким образом, с одной стороны, каждой модели (и реальной ОС) принцип оптимальности Rε ставит в соответствие (см. рисунок 1а) множество стратегий, которые ε-оптимальны в данной модели (данной реальной ОС). С другой стороны, каждому управлению u Î U можно поставить в соответствие (см. рисунок 1б) множество B(e, u) моделей (реальных ОС), в которых данное управление ε- оптимально. Отметим, что в обоих случаях величина e является параметром (см. рисунок 1) и на обоих рисунках (1а и 1б) модель m~ Î M, ОС m Î M и управление u Î U одни и те же.

12

~	~				M
	Mε1 (m)		m
m		Mε2 (m)
~			M	ε1	(m)
Mε 2 (m)

U

Rε2 (m~) u Rε2 (m)

Rε1 (m~) Rε1 (m)

Рис. 1а. Множества e-оптимальных решений (e1 ³ e2 ³ 0)

M

m~ B(ε2, u) m

B(ε1, u)

U

u

Рис. 1б. Области абсолютной устойчивости решения uÎU (e1 ³ e2 ³ 0)

13

Перейдем к определению адекватности. Фиксируем некоторую модель m~ Î M и принцип оптимальности Rε. Интуитивно понятно, что при e = 0 адекватность соответствует, в отличие от устойчиво-

сти (когда требуется непрерывность sup K(t, m) по модели [32]),

t U

непрерывности по модели из малой окрестности m~ следующей функции: K(u, m), u Î Rε( m~ ). Поэтому можно считать, что модель m~ с принципом оптимальности Rε e-адекватна (в смысле задачи полного выбора [32]) множеству реальных ОС Mε( m~ ), определяе- мому следующим образом:

(5) Mε( m~ ) = {m Î M | Rε( m~ ) Ç Rε(m) ¹ Æ} Í M,

то есть тем реальным ОС, в которых хотя бы одно из решений, оптимальное в модели, также оптимально. На рисунке 1а показан случай, когда m Ï Mε2 (m~) , но m Î Mε1 (m~) .

Другими словами, модель m~ с принципом оптимальности Rε ε-адекватна множеству реальных ОС Mε( m~ ), если $ u Î U: m Î B(e, u), m~ Î B(e, u) (см. рисунок 1б). Еще один эквивалентный способ формулировки того же определения следующий: Mε( m~ ) Ç Mε(m) ¹ Æ. Следовательно, адекватность модели опреде- ляется через абсолютную устойчивость оптимальных в ней реше- ний.

Отметим, что определение (5) симметрично относительно ре-

				~
альной ОС и ее модели, поэтому можно считать, что модель m e-
адекватна реальной	ОС m,	если	~
			m Î Mε(m). Понятно, что
~	~	Í Mε 2	~	~
" m Î M, "e1 ³ e2 ³	0 M0( m )		(m) Í Mε1	(m) .

Совокупность решений (с параметром e ³ 0): {u Î U; B(e, u)} в [37] названа обобщенным решением задачи управления. Совокуп- ность {u Î Rε( m~ ); B(e, u)} является обобщенным решением задачи управления для модели m~ Î M.

Следует отметить, что приведенное определение адекватности слишком широко, так как в нем фигурирует множество всех ε- оптимальных (для модели или реальной ОС) решений.

Следовательно, для каждого решения u Î U, помимо его эф- фективности (эффективности управления, «допустимое» отклоне-

ние которого от максимального значения определяется параметром

14

ε), существует еще одна характеристика – множество тех ОС B(e, u), в которых оно ε-оптимально, то есть абсолютно устойчиво.

Областью e-адекватности модели m~ Î M назовем следующее

~	I~	B(e, u), то есть множество тех ОС,
множество ОС: M( m , e) =
	u Rε (m)

для которых любое решение, ε-оптимальное в модели, также явля- ется ε-оптимальным. Аналогичным образом можно определить область ε-адекватности реальной ОС m Î M:

M(m, e) = I B(e, u).

u Rε (m)

Итак, появляется возможность сравнения оптимальных реше- ний. Естественно считать, что из двух решений, удовлетворяющих принципу оптимальности, решение, эффективное в большей облас- ти ОС, "лучше". Введем на множестве Rε( m~ ) следующее отноше-

ние "Ð" (в общем случае не полное):

(6) " e ³ 0 " u1, u2 Î Rε( m~ ) u1 Ð u2 « B(e, u1) Í B(e, u2).

Понятно, что с точки зрения практического использования резуль-

татов математического моделирования целесообразен выбор из Rε( m~ ) элемента, максимального по отношению "Ð" (если таковой существует).

Итак, для фиксированных модели и принципа оптимальности можно указать множество реальных ОС (множество моделей ОС), в которых существует решение, гарантированно удовлетворяющее принципу оптимальности. Это множество заведомо не пусто, так как содержит саму модель (см. рисунок 2).

15

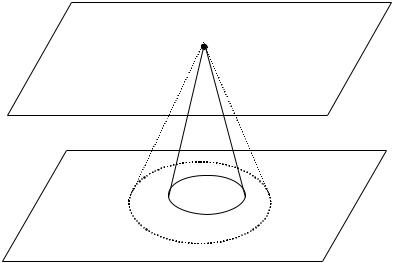
M

m~

M

M( m~ , ε2)

M( m~ , ε1)

Рис. 2. Области адекватности (e1 ³ e2 ³ 0)

Если существует решение, ε-оптимальное в модели, которое ε- оптимально и в реальной ОС, то будем считать, что модель ε- адекватна. Таким образом, критерием ε-адекватности модели является эффективность управления реальной ОС.

Знание множества B(e, u), u Î Rε( m~ ), позволяет на этапе вне- дрения результатов анализа модели m~ оценить возможные потери от практического использования решения и, быть может, при необходимости, пересмотреть модель ОС или принцип оптималь- ности.

Модификация принципа оптимальности даже при фиксиро- ванных параметрах модели представляется достаточно перспек- тивной. Например, снижая требования к эффективности управле- ния, можно для каждого из решений расширить область его устойчивости и, следовательно, расширить множество реальных ОС, в которых решения, удовлетворяющие ослабленному принци- пу оптимальности, будут гарантированно оптимальными (точнее, в классической терминологии – гарантированно ε-оптимальными).

16

Приведенные качественные рассуждения свидетельствуют,

что существует определенный дуализм между эффективностью решения задачи управления и областью его гарантированной при- менимости (областью его абсолютной устойчивости или областью адекватности). Конкретные зависимости между эффективностью и областью адекватности для ряда моделей ОС приведены в [37].

Жертвуя эффективностью управления, можно расширить множество ОС, в которых применимы результаты моделирования.

Особенно ярко этот эффект проявляется при анализе областей устойчивости решений, удовлетворяющих тем или иным критери- альным принципам оптимальности. Величина ε, фигурирующая в определении критериального принципа оптимальности, фактиче- ски, характеризует те потери эффективности, на которые мы гото- вы пойти, считая решение еще «оптимальным» (такое общее опре-

деление оптимальности несколько противоречит широко распространенному определению, в соответствии с которым опти- мальным считается допустимое решение, имеющее максимально возможную эффективность).

Качественно отмеченный выше дуализм между эффективно- стью и адекватностью (областью устойчивости) для критериальных принципов оптимальности имеет следующий формальный вид: множество ОС, адекватных фиксированной модели с критериаль- ным принципом оптимальности, не уменьшается с ростом ε; кроме того, область абсолютной устойчивости фиксированного решения, оптимального в модели, не сужается с ростом ε [37,40]. Данный факт (с ослаблением требований к эффективности некоторого решения область его абсолютной устойчивости расширяется и, следовательно, расширяется область адекватности) свидетельству- ет, что для решения проблем устойчивости и адекватности доста- точно указать конкретную зависимость между величиной ε и мно- жеством ОС, котором требуется обеспечить заданную эффективность управления, то есть, например, найти по модели минимальное значение ε, обеспечивающее выполнение требования адекватности.

Отметим, что во многих случаях [37] области абсолютной ус- тойчивости оптимальных (при ε = 0) решений задач управления очень узки и иногда состоят из одной точки. Возможность расши-

17

рения областей устойчивости "неустойчивых" решений, установ- ленная выше и в [32, 37, 40, 75], свидетельствуют, что критерий ε- оптимальности является регуляризирующим (в смысле [53]) для критерия K(u, m).

Таким образом, мы привели известные подходы к определе- нию понятий устойчивости решений задач управления ОС и адек- ватности моделей ОС реальным системам. Конструкцией, которая использовалась при этом, явилось понятие обобщенного решения, включающего в себя в явном виде зависимость между эффективно- стью управления и областью его устойчивости и адекватности.

Приведенная методология может быть использована и для анализа проблем унификации управления проектами.

В заключение настоящего раздела определим, что будет пони-

маться под эффективностью типового решения.

Пусть имеется ОС m Î M и ее модель m~ Î M. Определим ми- нимальную величину e(m, m~ ) потерь эффективности, при которой существует хотя бы одно решение, которое e(m, m~ )-оптимально и в модели, и в ОС:

(7) e(m, m~ ) = min {e ³ 0 | M( m~ , e) Ç M(m, e) ¹ Æ}.

Если задано множество ОС M1 Í M, то можно определить для заданной модели m~ Î M минимальную величину потерь в эффек- тивности e( m~ , M1), при которой любое решение, e( m~ , M1)- оптимальное в модели будет гарантированно e( m~ , M1)- оптимальным во множестве реальных ОС M1:

(8) e( m~ , M1) = min {e ³ 0 | M1 Í M( m~ , e)}.

Величина (8) может рассматриваться как критерий «качества» модели m~ Î M. Следовательно, для заданного класса ОС M1 мож- но ставить задачу поиска наилучшей модели, то есть модели, кото- рая давала бы максимальное гарантированное значение эффектив- ности управления:

(9) m~ (M1) = arg min e( m~ , M1).

~ m M

Минимальные потери эффективности, которые достигаются при использовании «оптимальной» модели (9), равны:

(10) e(M1) = min e( m~ , M1).

~ m M

18

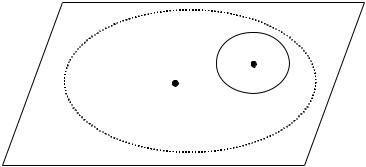
Понятно, что M2 M1 M ε(M2) ≤ ε(M1) ≤ ε(M), то есть с расширением класса ОС, для которого решается задача синтеза

управлений, гарантированная эффективность не возрастает. Так как множество реальных ОС, фигурирующее в выражении (10), отражает ту информацию о моделируемом объекте, которой обла- дает исследователь операций, то сделанный вывод можно пере- формулировать следующим образом: с ростом информированности (с уменьшением неопределенности) гарантированная эффектив- ность управления не убывает, что вполне согласовано с результа- тами, приведенными в [39].

Отметим, что эффективность управления (10) существенно за- висит от той априорной информации, которую имеет исследова- тель операций, то есть от множества M1. Если в течение времени поступает новая более точная информация M2 M1 о том классе ОС, которому принадлежит моделируемая система, то, используя эту новую информацию, можно уточнить модель, то есть перейти от модели m~ (M1) к модели m~ (M2), что даст возможность повы- сить гарантированную эффективность управления: ε(M2) ≤ ε(M1) (см. рисунок 3).

M

~	~
	m (M2)
m (M1)	M2
	M1

Рис. 3. Повышение гарантированной эффективности управления

с ростом информированности

19

4. Обобщенные решения в управлении проектами: агрегирование информации

В настоящем разделе рассматривается применение приведен-

ных выше общих результатов построения и анализа обобщенных решений к такой задаче управления проектами как агрегирование информации (см. описание задач календарно-сетевого планирова- ния и управления с агрегированием информации в [5, 6, 9, 14]).

4.1. Описание модели

Рассмотрим модель проекта – многоэлементную детерминиро- ванную двухуровневую организационную систему (ОС), состоя- щую из центра – руководителя проекта – и n исполнителей – ак- тивных элементов (АЭ). Стратегией АЭ является выбор действий, стратегией центра – выбор функции стимулирования, то есть зави- симости вознаграждения каждого АЭ от его действий и, быть может, действий других АЭ или других агрегированных показате- лей их совместной деятельности.

Обозначим yi Ai – действие i-го АЭ, i I = {1, 2, …, n} –

n
множество АЭ, y = (y1, y2, ..., yn) A' = ∏ Ai	– вектор действий
i=1
АЭ, y-i = (y1, y2, …, yi-1, yi+1, …, yn) A-i = ∏ Aj	– обстановка игры
j¹i

для i-го АЭ.

Пусть результат деятельности z A0 = Q(A’) ОС, состоящей из n АЭ, является функцией (называемой функцией агрегирования) их действий: z = Q(y). Интересы и предпочтения участников ОС – центра и АЭ – выражены их целевыми функциями. Целевая функ- ция центра является функционалом Φ(σ, z) и представляет собой разность между его доходом H(z) и суммарным вознаграждением

n

υ(z), выплачиваемым АЭ: υ(z) = åσ i (z) , где σi(z) – стимулирова-

i=1

ние i-го АЭ, σ(z) = (σ1(z), σ2(z), …, σn(z)), то есть

20