Metodichki / Векторная алгебра

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ВЕКТОРНАЯ АЛГЕБРА Практикум

Методические указания по проведению практических занятий для студентов технических специальностей

Владивосток 2012

Одобрено методическим советом университета УДК 519

Практические занятия по курсу векторной алгебры.: метод. указания / Сост. Н.Е. Дегтярева. – Владивосток: Изд-во ДВФУ, 2012 – 28с.

В краткой форме излагается основной теоретический материал, входящий в раздел векторной алгебры: понятие вектора и линейных действий над векторами, скалярного, векторного и смешанного произведения векторов основные свойства. Содержит 10 вариантов заданий для самостоятельной работы студентов. Приведены решения типовых заданий и список дополнительных задач.

Методические указания предназначены для студентов технических специальностей.

Методические указания печатаются с оригинал-макета, подготовленного автором

©Н.Е.Дегтярева

©Изд.-во ДВФУ, 20102

2

1.1

Векторы. Линейные операции над векторами.

Деление отрезка в данном отношении.

Вектором называется направленный отрезок у которого известны

A и

B. Обозначается АВ,

Через

точка начала

точка конца

AB

.

BA

обозначают вектор, направленный противоположно вектору

AB

.

Если заданы

координаты

точек

начала

A1(x1,

y1, z1)

и конца

A2(x2, y2, z2) вектора

, то

координаты

вектора

определяются по

AB

формуле:

(x2 x1,

y2 y1, z2 z1)

AB

(1.1)

Модулем или длинной вектора называют расстояние между его началом

. Если

ax; ay; az , то

AB

и концом и обозначают

AB

ax2

a2y

az2

AB

(1.2)

Векторы, параллельные некоторой прямой, называются коллинеарными. Векторы, параллельные одной плоскости, называются компланарными.

Два вектора называются равными, если они: 1)коллинеарны, 2) соноправленны, 3) равны по длине.

Произведением вектора

ax; ay; az на вещественное число

а

называется

вектор

a

длина которого

равна

b

a

,

а

b

направление

совпадает с направлением вектора

a

,

если 0,

и

противоположно ему, если 0. Координаты вектора определяются по формуле:

b

a

( ax; ay; az )

(1.3)

Т.е. при умножении вектора на число, каждая его координата умножается на это число.

Суммой векторов a1, a2,..., an называется вектор, обозначаемый a1 a2 ... an, начало которого находится в начале первого вектора a1, а

конец в конце последнего вектора an ломанной линии (правило замыкания ломанной). (Рис. 1.1).

a2

a3 a4 a5

a1

a1 a2 ... a5

Рис. 1.1

3

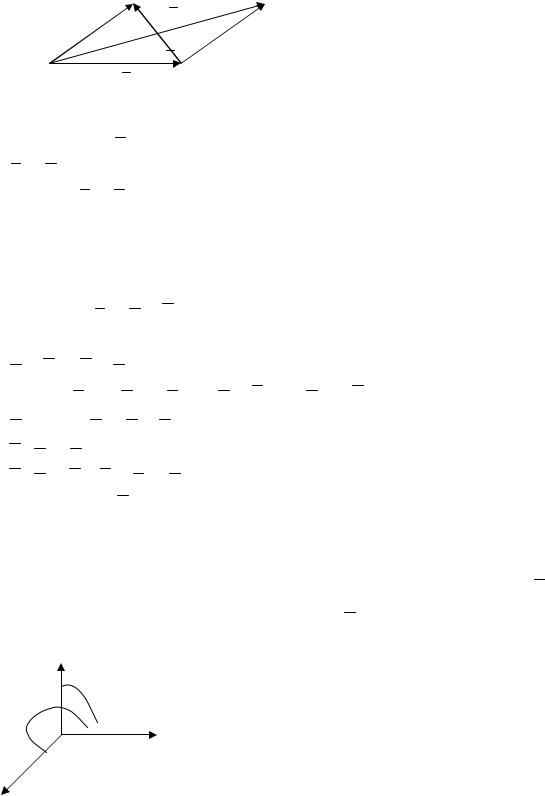
В случае суммы двух векторов оно равносильно

правилу

параллелограмма (Рис. 1.2).

a

b

b

a

b

a

Рис. 1.2

Если векторы

a

и

заданы своими координатами, то координаты

b

вектора

c

a

b

определяются по формуле :

c

a

b

(ax bx; ay by; az bz )

(1.4)

т.е. при сложении векторов их соответствующие координаты складываются.

Аналогично определяется разность векторов, как разность соответствующих координат:

c

a

b (ax bx; ay by; az bz )

(1.5)

Линейные операции над векторами удовлетворяют свойствам:

1. a b b a - коммутативность;

2. a a a, a b a b - дистрибутивность;

3.a 1 a a a 0;

4.1 a a ;

5.0 a 0 , 0 a a.

Всякий вектор a образует с координатными осями Ox, Oy, Oz углы

, , -соответственно. Углы связаны соотношением:
cos2 cos2 cos2 1	(1.6)

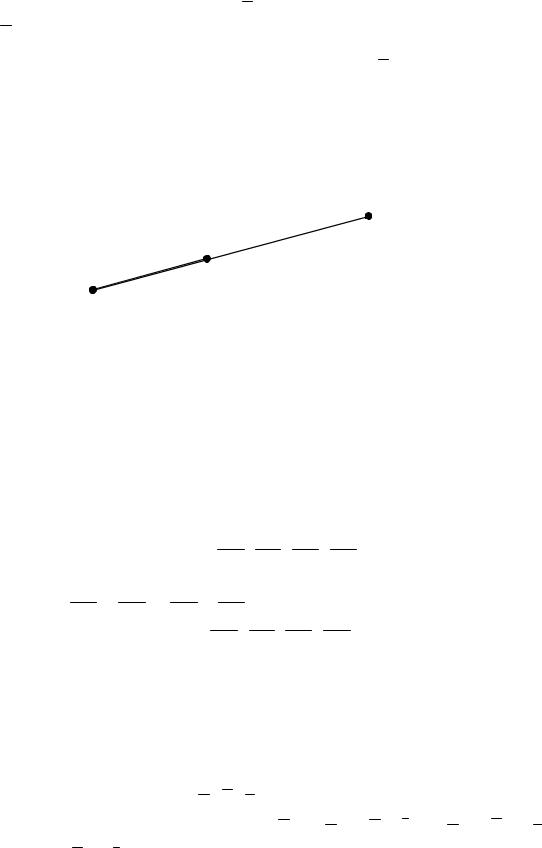
cos , cos , cos - называются направляющими косинусами вектора a и

являются координатами нормированного вектора a0.(Рис. 1.3)

z

y

x

Рис. 1.3

4

a

x

ay

a

z

a0 (cos ; cos ; cos )

;

;

(1.7).

a

a

a

Произвольный вектор

a

можно

записать

в

координатной

форме

a

ax; ay; az

или

линейной комбинацией

базисных векторов

i

(1; 0; 0),

j

(0;1; 0), k (0; 0;1):

a

axi

ay

j

azk

M x,

y, z

M1M2

Отношение

, в котором

точка

делит отрезок

(Рис. 1.4) удовлетворяет равенству

M1M

MM2

(рис.1.4).

M2 x2;y2;z2

M x;y;z

M1 x1;y1;z1

Рис. 1.4

которое задается соотношением:

x

x1

x2

,

y

y1

y2

, z

z1 z2

(1.8).

§1.2 Практикум.

1.1.Даны координаты точек A и B. Вычислить:

1)координаты векторов AB, BA, OA, OB, где точка O– точка начала координат;

2)найти OA OB и OB OA сравнить результаты с п.1;

3)найти модули векторов AB, BA, OA, OB.

1)	A(3; 2),	B(2; -1);	2)	A(-3; 1), B(-2; 5);
3)	A(4; -1), B(3; -2);		4)	A(-1; 2), B(3; 8);
5)	A(5; 4),	B(-3; 1);	6)	A(9; -3), B(7; 4);
7)	A(2; 7),	B(-1; 5);	8)	A(-1; 4), B(5; 3);
9)	A(-3; 5), B(4; -2);		10) A(7; -2); B(5; -3).

1.2.Даны векторы a, b, c . Вычислить:

1)координаты и модуль векторов d 2a 4b , f a 3b 3c записать векторы d и f линейной комбинацией базисных векторов;

5

2)векторы a и b являются сторонами параллелограмма. Найти длину его диагоналей (использовать действия сложения и вычитания векторов

(рис 1.2));

3)найти направляющие косинусы вектора c.

1)	a				(1; 1; 0),					b (0; 7; 4),															c			( 1; 2; 6);
2)			a		( 3; 5;1),						b									(4; 2; 1),								c			(6;5; 3);
3)			a		(3,1, 2),										b						(5, 3,8)					,			c		(1, 4, 6);
4)			a		(1, 1, 0),							b							(2, 7, 4)					,		c			(5, 3, 1);
5)			a		(0, 2, 1),																b		(3, 7,	5)						,		c	(4, 2, 1);
6)			a		(7,8, 0),				b						( 4, 3, 5)									,		c			(1, 2, 3);
7)			a		(5,1, 0),			b							(7, 2,1)									,		c			(3, 4, 5);
8)			a		( 5, 2, 0),										b					(6, 3, 1),									c	(7, 4, 2);
9)			a		(1, 3,8),									b					(2, 4,1),										c	( 1, 0, 3);
10)				a		(4, 9,1),													b			(5, 3, 2),											c	( 4, 0, 5);

1.3.Вектор AB составляет с координатными осями Ox,Oy,Oz углы

, , соответственно. Вычислить координаты вектора AB, если:

1)

300,

1200,

AB

2;

2)

600,

300,

AB

3;

3)

300, 1200,

4;

4)

300,

600,

2;

AB

AB

5)

1200, 600,

4;

6)

600, 300,

2;

AB

AB

300, 1200,

3;

1200,

300,

4;

7)

AB

8)

AB

1200, 300,

2;

30 0 , 600,

4;

9)

AB

10)

AB

1.4. Даны две вершины A и B параллелограмма ABCD и точка

пересечения его диагоналей E. Найти:

1) координаты остальных вершин;

A

B

2)

отрезок

ограниченный

точками

и

разделен точками

M1, M2, M3, M4

на пять равных

частей.

Найти координаты точек

Mi, M j.

1)

A(7, 8, 0),

B( 4, 3, 5),

E(1, 2, 3),

i 3,

j 4;

2)

A(3, 5, 7),

B(4,1, 2),

E( 2, 0, 1),

i 2,

j 3;

3)

A( 3, 5,1),

B(6, 5, 3),

E(4, 1, 2),

i 1,

j 4;

4)

A(5, 3, 1),

B(2, 4, 7),

E(0, 1,1),

i 1,

j 3;

5)

A(5,8, 3),

B(4,1, 6),

E(1, 2, 3),

i 2,

j 4;

6)

A(7, 0, 4),

B(2, 5, 3),

E( 2, 6, 1),

i 2,

j 3;

6

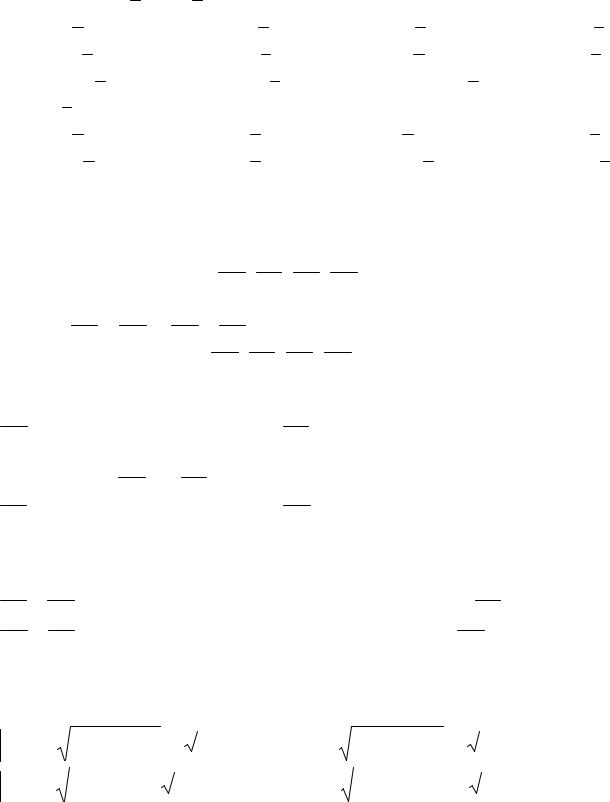
7)	A(5, 3, 2),		B(1, 9, 4),		E( 4, 0, 5),		i 1,	j 4;
8)	A( 3,1,8),	B(1, 2, 4),		E(0, 3, 1),		i 3,		j 4;
9)	A(6, 1, 3),		B(2, 0, 5),		E(7, 2, 4),		i 1,	j 2;

10) A(7, 2, 1),

B(3, 5, 4),

E(5,1, 0), i 1,

j 3.

1.5. Векторы

,

служат сторонами треугольника ABC.

AB

,

BС

СA

Выразить через

a

,

и

c

векторы, совпадающие с медианами треугольника:

b

a

,

2

,

СA

3

c

;

AB

a

,

BС

2

,

СA

c

;

1)

AB

BС

b

2)

b

AB

3

a

BС

2

c

AB

2

a

BС

3

,

c

;

3)

,

b

,

СA

;

4)

,

b

СA

AB

2

a

BС

3

,

2

c

;

AB

3

a

,

BС

2

,

5)

,

b

СA

6)

b

СA

c

;

7)

AB

a

,

BС

,

СA

2

c

;

8)

AB

a

,

BС

2

,

СA

2

c

;

b

b

9)

AB

4

a

,

BС

,

СA

c

;

10)

AB

2

a

,

BС

,

СA

3

c

.

b

b

§1.3 Решение типового задания.

1.1.Даны координаты точек A(4, 2) и B( 1, 3). Вычислить:

1)координаты векторов AB, BA, OA, OB, где точка O– точка начала координат;

2)найти OA OB и OB OA сравнить результаты с п.1;

3)найти модули векторов AB, BA, OA, OB.

Решение:

1) Вычислим координаты векторов используя формулу (1.1)

AB ( 1 4;3 2) ( 5;1),

BA (4 ( 1); 2 3) (5; 1).

Вывод: противоположно направленные векторы отличаются знаком своих

координат т.е. AB BA
OA (4 0; 2 0) (4; 2),	OB ( 1 0; 3 0) ( 1, 3).

Вывод: координаты радиус-вектора точки совпадают с координатами самой точки.

2) Найдем разность векторов, используя формулу (1.5)

OA OB (4; 2) ( 1, 3) (4 ( 1); 2 3) (5; 1) BA;

OB OA ( 1; 3) (4; 2) ( 1 4;3 2) ( 5;1) AB.

Вывод: разность радиус-векторов точек дает координаты вектора противоположно направленного вектору построенному на этих точках.

3) Вычислим модули векторов по формуле (1.2):

AB				( 5)2 12				26	,		BA		52 ( 1)2			26			;
																		.
				42 22										( 1)2 32
ОА						20	,				ОВ						10

7

Вывод: модули противоположных векторов равны.

1.2. Даны векторы a (1; 1; 0), b (3; 2; 1), c (4; 5;1).

Вычислить:

1) координаты и модуль векторов d 2a 4b , f a 3b 2c записать

векторы d и f линейной комбинацией базисных векторов;

2)векторы a и b являются сторонами параллелограмма. Найти длину его диагоналей (использовать действия сложения и вычитания векторов (Рис

1.2));

3)найти направляющие косинусы вектора c.

Решение:

1) Вектора d и f заданы линейной комбинацией векторов a и b , которые в свою очередь заданы координатами. Подставим в линейные комбинации заданные координаты:

d 2a 4b 2 (1; 1; 0) 4 (3; 2; 1) (2; 2; 0) (12;8; 4)(2 12; 2 8; 0 ( 4)) (14; 6; 4).

Мы нашли координаты вектора d , запишем его линейной комбинацией базисных векторов декартовой системы координат:

d (14; 6; 4) 14i 6j 4k .

Найдем его модуль: d 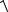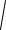142 62 ( 4)2 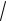248.

Аналогично вычисляем координаты и модуль вектора f

f a 3b 2c (1; 1; 0) 3 (3; 2; 1) 2 (4; 5;1)

( 1;1; 0) (9; 6; 3) (8;10; 2)

( 1 9 8;1 6 10; 0 ( 3) 2) (0; 3; 5);

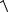
f a 3b 2c (0; 3; 5) 3j 5k ; f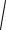( 3)2 ( 5)2 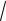34.

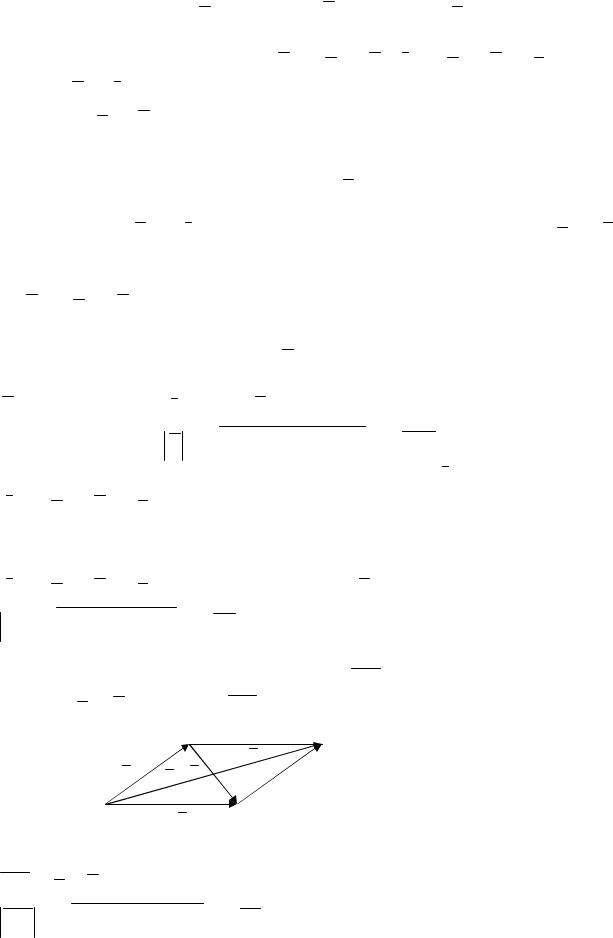
2) Для определения длины диагоналей, найдем координаты векторов,

их представляющих (рис. 1.5). Диагональ AC представляет из себя сумму

векторов a и b . Диагональ BD - разность этих векторов.

B C

a b

b

a

b

A D a

Рис. 1.5

AC a b (1 3; 1 2; 0 ( 1)) (4;1; 1);

AC 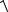42 12 ( 1)2 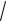18;

8

BD a b (1 3; 1 2; 0 ( 1)) ( 2; 3;1);

BD 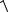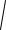( 2)2 ( 3)2 12 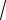14.

3) Для определения направляющих косинусов вектора c используем формулу (1.7)

cos	cx				,		cos				cy								,				cos								cz					.
		c											c																				c
								c				с										42		52					12													.
Вычислим модуль вектора									:																														42
Тогда, cos					4		, cos				5									, cos									1				.
					42						42																42
Проверка: cos2 cos2 cos2																							4							2								5 2
																									42													42

		1				2
						1.
		42

1.3. Вектор AB составляет с координатными осями Ox,Oy,Oz углы

, , соответственно. Вычислить координаты вектора AB, если: 600,

300, AB 5.

Решение:

(x,

y, z), используя направляющие

Найдем

координаты

вектора

AB

косинусы. Нам известно, что:

cos

x

cos

y

cos60

0

1

,

,

2

AB

AB

cos												z					cos300								3		;
																									2
											AB
Определим																значение cos :
																															1		1				3
cos													1 cos2 cos2																												0;
																															4			4								1		5
x								cos 5 0 0,																								y									cos 5
				AB																																AB									;
																								5						.											2		2
z							cos 5													3							3
				AB
																			2												A(2,1, 3)										и B( 1, 0,1)
																									2
				1.4.
													Даны две						вершины																								параллелограмма

ABCD и точка пересечения его диагоналей E(1, 1, 2). Найти: 1) координаты остальных вершин;

9

2) отрезок,	ограниченный			точками	A и	B,	разделен точками
M1, M2, M3, M4		на	пять	равных	частей.	Найти	координаты точек
Mi, M j, если	i 1,	j	4.
Решение:
1) Точка	пересечения диагоналей, делит					последнюю пополам (см.

рис.1.5). Используем формулу деления отрезка пополам. Тогда для диагонали

AC имеем x	E		xA xC	, откуда	x	2x	E	x	A	. Для диагонали
		2			C

BD: xE xB xD , откуда xD 2xE xB.
2
Аналогичные формулы получаем для координат yи z точек Cи D.
xC 2 1 2 0,	yC 2 ( 1) 1 3,	zC 2 2 3 1;
xD 2 1 ( 1) 1,	yD 2 ( 1) 0 2,	zD 2 2 1 3.

Таким образом, вершины C и D имеют координаты: C (0, 3,1) и

D(1, 2, 3).

2)Точка M1 делит отрезок AB в отношении один к четырем (рис. 1.6), т.е.

AM1		1	,		1,		4. Точка M		делит отрезок AB в отношении
M1B 4				1		1		4

четыре к одному т.е. AM4 4, 2 4, 2 1.

M4B 1

M3 M4

B

M2

M1

A

Рис. 1.6

Используя формулу деления отрезка в данном отношении (1.8), получим координаты искомых точек:

x	M1			1xA 1xB			4 2 1 ( 1)						7	;
				1 1				4 1	5
y	M1			1yA 1yB				4 1 1 0		4		;
				1 1				4 1	5

10