ГСХ 2013лекции / ГСХ 2013 / ГСХ студент / Три задания / 2.РВПСГ / Теор.вероятн

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ

1.Определение случайной величины. Случайная величина – это такая величина, точное значение которой в каждый конкретный момент можно определить с некоторой долей уверенности (с некоторой вероятностью). Такое положение возникает из-за воздействия случайным образом разнообразных факторов на изучаемый процесс. Случайное воздействие этих факторов в конечном итоге порождает неопределенность, т.е. невозможность однозначно и точно определить развитие событий и состояние исследуемого параметра – случайной величины.

2.Частота возникновения или вероятность.

Изучается строительство однотипных объектов. Количество объектов N. Изучается время выполнения однотипных по составу и объему работ. В результате действия случайных факторов продолжительность выполнения t изучаемой работы на различных объектах может быть различной.

Продолжительность работы (событие)	t1	t2	t3	t4	……
Количество выявленных случаев	n1	n2	n3	n4	……

Понятно, что сумма выявленных случаев равна количеству объектов N, т.е.

Σn_i = N

В приведенную таблицу вместо количества выявленных случаев введем частоту их появления или вероятность b.

Тогда таблица преобразуется к виду:

Продолжительность работы (событие)	t1	t2	t3	t4	……
Частота появления (вероятность)	b1	b2	b3	b4	……

Понятно, что сумма вероятностей равна 1, т.е.

Σ b_i = 1

Значение вероятности находится в пределах 1 ≥ b ≥ 0

Величину У, равную У = 1- b определим как уровень риска.

Тогда имеем:

Событие	Вероятность b	Уровень риска У
Достоверное	1	0
Неосуществимое	0	1

3.Нормальный закон (закон Гаусса) распределения случайной величины .

Теоретически доказано и практически подтверждено, что продолжительность работы и продолжительность строительства как случайные величины подчиняются нормальному закону распределения (закону Гаусса). Это наиболее часто встречающийся на практике закон распределения. Главная его особенность состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Кривая распределения по нормальному закону имеет симметричный холмообразный вид.

График кривой распределения показывает, что имеется некоторое значение средней величины с наибольшей вероятностью появления, чем другие. Остальные значения случайной величины подвержены некоторому разбросу относительно ее среднего значения. Понятно, что, чем меньше величина этого разброса, тем более определенным будет изучаемый процесс (выполнение конкретной работы).

-3σ t_р +3σ Продолжительность

Этот рисунок в графической форме отражает зависимости, описываемые таблицами в п.2.

4.С практической точки зрения при изучении случайных процессов необходимо прежде всего определить три параметра:

4.1.Значение средней величины;

4.2.Мера разброса случайной величины относительно ее среднего значения;

4.3.Вероятность того, что случайная величина по своему значению не выйдет за определенный предел (будет находится в интересующем нас интервале).

4.1.Значение средней (расчетной) величины

Средняя величина называется математическим ожиданием случайной величины. Это сумма произведений всех возможных значений случайной величины на вероятности этих значений.

t_р = t_ср = Σ (t_i * b_i)

4.2.Мера разброса случайной величины относительно ее среднего значения

Для характеристики меры разброса значений случайной величины вводится параметр – среднее квадратическое отклонение σ (сигма).

Для того, чтобы уяснить смысл этого понятия рассмотрим возможные способы оценки величин разброса значений случайной величины. Рассмотрим для этого два примера, характеризующие разброс случайной величины. В примерах рассматриваются по 6 значений случайной величины.

1. -15 -10 -5 0 +5 +10 +15

2. -20 -15 -10 0 +10 +15 +20

Понятно, что во втором примере степень разброса выше, следовательно, должно быть больше значение среднего отклонения.

Вариант1. Суммируем с учетом знака все значения отклонений и делим на 6 (число значений). В обоих случаях получаем 0. Такой вариант не подходит.

Вариант2. Суммируем без учета знака все значения величин и делим на 6 (число значений.) В первом примере получаем 10, а во втором 15. Этот вариант плох тем, что математическая обработка полученных величин трудно реализуется.

Вариант3. Среднее квадратическое отклонение. В этом случае используется эффективный математический аппарат для последующей обработки полученных данных.

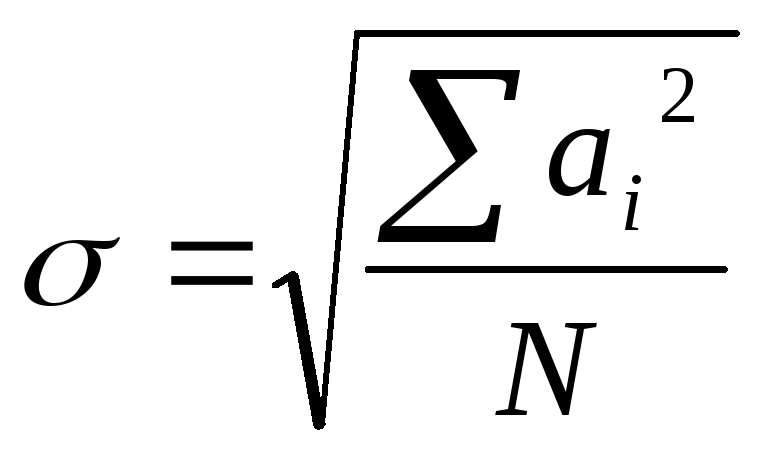
σ (сигма) – среднее квадратическое отклонение

a_i – отклонение случайной величины от среднего значения

N – число изучаемых случайных величин.

Квадратный корень вводится для того, чтобы случайные величины и среднее квадратическое отклонение имели бы одинаковую размерность. Например, если отклонения случайной величины измеряются в метрах (м), то, если удалить квадратный корень, то в этом случае величина среднего квадратического отклонения будет измеряться в квадратных метрах (м²).

Среднее квадратическое отклонение для первого примера равно:

Среднее квадратическое отклонение для второго примера равно:

ПРАВИЛО ТРЕХ СИГМ

При нормальном законе распределения можно утверждать, что практически любое значение случайной величины будет находится в интервале: t_ср ± 3σ (см. график).

4.3.Вероятность того, что случайная величина по своему значению не выйдет за определенный предел (будет находится в интересующем нас интервале).

Интересующая нас вероятность определяется при анализе функции распределения нормального закона (закона Гаусса).

Нормальный закон связывает между собой значение случайной величины с ее вероятностью. Чаще всего рассматривается не сама случайная величина, а ее отношение к среднему квадратическому отклонению. Численные значения нормального закона распределения рассчитаны и сведены в специальные таблицы. Графически закон представляется приведенной ниже кривой.

Эта кривая позволяет ответить на вопрос: какова вероятность того, что исследуемая случайная величина окажется в интересующем нас диапазоне? Или этот вопрос может быть сформулирован несколько иначе: какова вероятность того, что случайная величина не превысит интересующего нас значения. Можно говорить не о вероятности, а о уровне риска (У). Потому что эти величины связаны зависимостью:

b = 1- У

Используя расчеты, строим график вероятности выполнения срока строительства. Расчеты выполняются в задании № 3, расчетная таблица 1. Исходными данными являются расчетные данные, полученные в задании № 2.

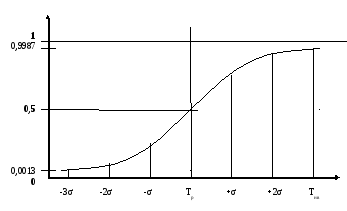
Из графика видно, что если установить срок выполнения равным Т_р - 3хσ(Т_кр), то вероятность его фактического выполнения будет близка к нулю, а при наиболее вероятном сроке Т_нв = Т_р + 3хσ(Т_кр) вероятность выполнения близка к единице.