Определение потерь напора при турболентном режиме движения. График Никурадзе
Основной расчетной формулой для потерь напора при турбулентном течении в круглых трубах является формула Дарси-Вейсбаха (7.2), которую мы с Вами уже получили на этой лекции.
Эта формула применима, как при турбулентном режиме течения, так и при ламинарном, различие заключается лишь в значениях коэффициента λ.
В турбулентном потоке при Re > Reкр потери напора на трение по длине значительно больше, чем при ламинарном. Если при ламинарном течении потеря напора на трение возрастает пропорционально скорости в первой степени, то при турбулентном заметен скачек сопротивления по закону, близкому к параболе второй степени (рис.7.3).
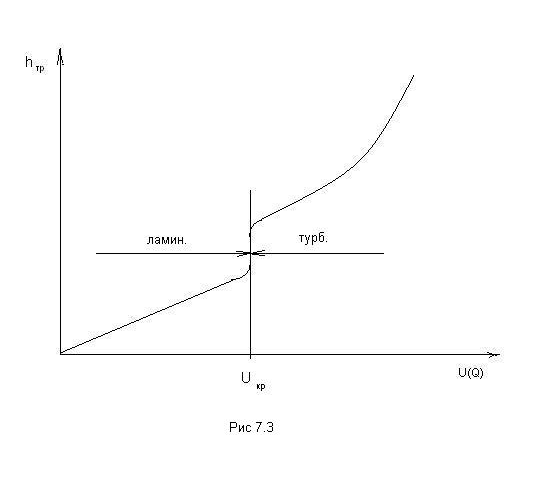
Как мы уже отметили, при турбулентном режиме течения наибольшие градиенты скоростей характерны для пристенного течения, то есть там наибольшие касательные напряжения и, следовательно, наибольшие потери энергии. Величина этих потерь и характер течения зависят от структуры потока в пристенном слое определяемой соотношением толщины этого слоя и средней высоты выступов шероховатости стенки. Если толщина вязкого подслоя δв.п. больше средней высоты выступов шероховатости Δ ,то такие поверхности называются гидравлически гладкими и в этом случае выступы покрываются вязким подслоем и потери энергии по длине практически не зависят от шероховатости (рис.7.4.а).
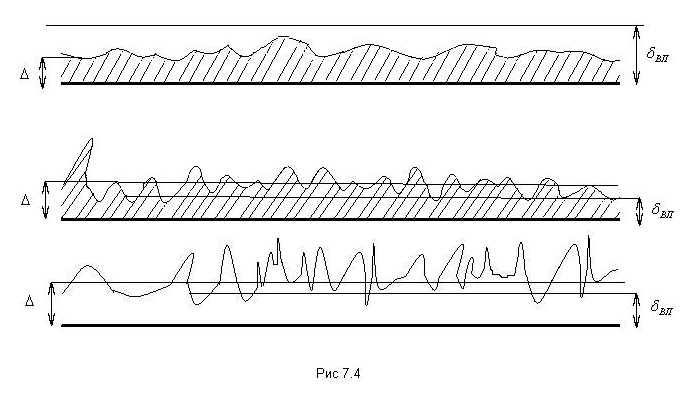
Если толщина δв.п. меньше высоты Δ, то поверхности называются гидравлически шероховатыми (рис.7.4.в) и потери зависят от шероховатости.
К сожалению, для определения коэффициента λ при турбулентном режиме движения нет теоретических решений и поэтому , он находится по эмпирическим формулам в зависимости от структуры турбулентного потока и от шероховатости стенок, которые характеризуются относительной шероховатостью Δ/ro, где ro – радиус трубы. Характер влияния этих двух параметров экспериментально исследовал И.Никурадзе в Германии в 1920 года. Никурадзе испытал на сопротивление ряд труб с различной шероховатостью при различных значениях чисел Re. Результаты этих испытаний представлены в виде графика (рис.7.5),который называется
Графиком Никурадзе.
Наклонными сплошными линиями показаны законами сопротивления для гладких труб при ламинарном “А” и турбулентном режимах течения. Коэффициент сопротивления λ для гидравлических гладких труб при турбулентном течении определяется по многим эмпирическим зависимостям, по самой распространяемой является формула Блазиуса.
λ=0.3164/Re^(+0.25)
Из рассмотрения графика Никурадзе можно сделать следующие выводы:
-
При ламинарном режиме течения шероховатость на сопротивление не влияет: штриховые линии совпадают с прямой “А.”
-
Критическое число Re от шероховатости практически не зависит: штриховые линии отклоняются от прямой “А” приблизительно при одном и том же Reк.р.
-
В области турбулентного течения, но при небольших Re и ∆/ro шероховатость на сопротивление не влияет: штриховые линии на некоторых участках совпадает с прямой “В”. Однако при увеличении Re это влияние начинает сказываться, и кривые для шероховатых труб начинают отклоняться от прямой “В”.
-
При больших Re и больших относительных шероховатостях коэффициент λ перестает зависеть от Re и становится постоянным для данной относительной шероховатости. То есть можно выделить три области значений Re и ∆/ro при турбулентном режиме течения:
а) Область малых Re и ∆⁄ro , где коэффициент λ не зависит от шероховатости, а определяется лишь числом Re . Это область гидравлически гладких труб.
б) Во второй области коэффициент λ зависит одновременно от двух параметров: Re и ∆⁄ro .
в) Область больших Re и ∆⁄ro , где коэффициент λ не зависит от Re, а определяется лишь относительной шероховатостью. Эту область называют областью автомодельности или областью квадратичного сопротивления, так как потеря напора пропорциональна скорости во второй степени.
Для практических расчетов по определению сопротивления реальных шероховатых труб можно пользоваться универсальной формулой Альтшуля:
∆т.=0.11*(∆экв.⁄α+68⁄Re)^¼,
где ∆экв. − эквивалентная областная шероховатость, α − диаметр трубы.
Тема 7. Вывод формулы Дарси-Вейсбаха.
Турбулентный режим течения.
Пульсация скорости. Определение потерь напора при турбулентном режиме движения. График Никурадзе
Вывод формулы Дарси-Вейсбаха
Преобразуем полученное нами на прошлой лекции выражение закона
Гагена-Пуазейля (6.7), выразив расход Q через произведение средней
скорости и площади поперечного сечения
(7.1)
для удобства использования зависимости (7.1) при решении практических
задач преобразуем ее следующим образом: коэффициент трения на единицу
длины (коэффициент Дарси), получим окончательно потери по длине
учитывая, что
, получим
.
Обозначая через
гидравлический
коэффициент трения на единицу длины
(коэффициент Дарси), получим окончательно,
что потери по длине
(7.2)
Зависимость (7.2) называется формулой Дарси-Вейсбаха и следует отметить,
что для ламинарного режима течения гидравлический коэффициент трения
получен теоретическим путем.
Турбулентный режим течения. Пульсация скорости
Турбулентный режим течения является более сложным для исследования, чем
ламинарный, вследствие интенсивного перемешивания жидкости, пульсации
скоростей и давлений. В настоящее время модель турбулентного потока
представляют состоящей из трех зон (рис.7.1):
Вязкого подслоя 1, переходной области 2 и области развитого течения или
ядра потока 3.
Вязкий подслой 1 располагается в непосредственной близости от стенок, в
нем наблюдаются турбулентные пульсации, но они заглушаются силами
вязкости. Поэтому в весьма тонком вязком подслое характер течения
обусловливается в основном вязким трением. Средняя толщина вязкого
подслоя может быть больше или меньше средней высоты выступов
шероховатости стенок.
В переходной области силы вязкости соизмеримы с силами инерции и здесь
наблюдается неустойчивый режим течения.
В ядре потока течение имеет четко выраженный турбулентный характер с
интенсивным перемешиванием жидкости.
Скорость и давление в любой точке турбулентного потока изменяются во
времени, причем беспорядочно, непериодически отклоняясь от некоторого
устойчивого среднего положения (рис.7.2). Поэтому мгновенную скорость
можно предусматривать
в виде двух составляющих:
-осредненная
по времени
и
-скорость пульсации, которая может быть
как со знаком «+», так и со
знаком «-». Тогда в общем случае можно записать
=
+
Введение понятия осредненной скорости позволило предложить осредненную
модель турбулентного потока, которая нашла широкое применение в
инженерной гидравлике. Для такой модели справедливы все результаты и
зависимости, полученные раньше. Это относится к уравнениям Бернулли,
неразрывности и т.д.
Распределение скоростей по сечению турбулентного потока носит более
сложный характер, чем при ламинарном. Эпюра скоростей носит
логарифмический характер и описывается выражением:
,
n зависит от Re для гидравлически гладких труб.
- осредненная во
времени локальная скорость;
-динамическая
скорость,
определяемая
выражением
,
где -
напряжение
турбулентного трения;
-плотность;
ǽ-постоянная Кармана, ǽ= 0,4; с - константа,
определяемая из условия, что максимальная осредненная скорость
находится в центре
потока, т.е. при
.
Тогда можно записать
(7.3)
Эпюра осредненных скоростей при турбулентном режиме течения
характеризуется следующими особенностями:
- скорости на поверхности стенки равны нулю;
- в пристенном слое на весьма малом расстоянии от стенки скорость
изменяется от нуля до значений, мало отличающихся от значений скорости в
центре потока;
- в ядре потока скорости изменяются относительно мало, а поэтому
мал и градиент скорости.
В связи с вышеупомянутым, коэффициент кинетической энергии или
коэффициент Кориолиса в уравнении Бернулли при турбулентном движении
принимаем равным
,
т.е. распределение скоростей более
равномерное.