Лекция 1. Математическое программирование. Понятие об оптимизационных задачах. Задача линейного программирования (злп). Графический метод решения злп. Симплекс-метод решения злп.

Вопросы:

1. Предмет – математическое программирование, краткая классификация методов.

2. Основные понятия теории оптимизации.

3. Постановка ЗЛП, различные формы записи. Примеры экономических задач.

4. Графический метод решения ЗЛП. Основные свойства ЗЛП.

5. Стандартная форма ЗЛП, правила построения.

6. Канонический вид ЗЛП, начальное допустимое базисное решение (НДБР),

метод искусственного базиса.

7. Симплекс-метод.

1. Предмет – математическое программирование.

Среди многочисленных проблем, возникновение которых связано с бурно развивающейся научно-технической революцией, пожалуй, наиболее важной является проблема совершенствования управления во всех звеньях хозяйства.

Современные промышленные предприятия, предприятия бытового обслуживания, транспортные агентства, научно-технические организации представляют собой сложные системы «человек-машина». Эффективность работы таких систем зависит от качества организационного управления. Чтобы добиться качества современному руководителю не всегда бывает достаточно личного опыта, интуиции и организаторских способностей в их традиционном понимании. При формировании стратегических и тактических решений руководитель должен учитывать множество подчас противоречивых соображений, опираться на сложные критерии эффективности путей достижения конечных целей. В связи с этим возникла необходимость применять для анализа и синтеза экономических ситуаций и систем математические методы и современную вычислительную технику. Такие методы объединяются под общим названием – математическое программирование.

Математическое программирование – область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т.е. задач на экстремум функций многих переменных с ограничениями на область изменения этих переменных.

Для того, чтобы успешно руководить крупным предприятием в условиях конкуренции руководителю, возможно, и не надо быть самому классным специалистом в области математического программирования, но чтобы понимать суть и смысл решаемой задачи, получаемых результатов и не «упустить руль», он должен понимать способ решения, быстро реагировать на возникающие изменения, чтобы эффективно использовать возможности математического программирования. Математическое программирование в настоящее время используется практически во всех областях жизни и производства:

• в экономике – для решения больших макроэкономических моделей (типа модели Леонтьева и др.), микроэкономических моделей или моделей предпринимательства, для оптимизации технико-экономических систем (планирование, эконометрика), транспортные задачи, в теории принятия решений, теории игр и т.п.;

• в технике – управление размерами и оптимизация структур, оптимальное планирование сложных технических систем, как информационные системы, сети компьютеров, транспортные и телекоммуникационные сети и др.;

• в автоматике – распознавание систем и объектов, оптимальное управление системами, фильтрация, роботы, автоматизированные линии и т.п.;

• в медицине, политике, социологии и т.п., и т.д.

Дадим ряд определений.

• Функцию, экстремальное значение которой нужно найти в условиях экономических возможностей, называют целевой, показателем эффективности или критерием оптимальности.

• Экономические возможности формализуются в виде системы ограничений.

Все это составляет математическую модель. Математическая модель – это отражение оригинала в виде функций, уравнений, неравенств, цифр и т.д.Модель задачи математического программирования включает:

• совокупность неизвестных величин х = (х₁, х₂, …, х_n), действуя на которые систему можно совершенствовать. Их называют планом задачи (вектором управления, решением, стратегией, поведением и т.п.);

• целевую функцию, которая позволяет выбрать наилучший вариант из множества возможных. Целевая функция обозначается F(x). Это может быть прибыль, объем выпуска или реализации, затраты производства, издержки обращения, уровень обслуживания или дефицитности и т.д.;

• условия (система ограничений), налагаемые на неизвестные величины. Эти условия следуют из ограниченности ресурсов, которыми располагает общество, из необходимости удовлетворения насущных потребностей, из условий производственных и технологических процессов. Математически ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений.

Т.о., модель задачи математического программирования примет вид:

Найти план х = (х₁, х₂, …, х_n), доставляющий экстремальное значение целевой функции F(x) →max(min), при ограничениях g_i(x) ≤ (=, ≥) b_i, i=.

Из экономических или физических соображений на план задачи или некоторые его компоненты, как правило, налагаются условия неотрицательности, х_j≥ 0, иногда – целочисленности.

План х, удовлетворяющий системе ограничений задачи, называют допустимым. Допустимый план, доставляющий целевой функции экстремальное значение, называют оптимальным. Оптимальный план обозначают х*, экстремальное значение функцииF(x*) =F*.

В зависимости от особенностей целевой функции F(x) и функций ограниченийg_i(x), задачи математического программирования делятся на ряд типов.

1. Задача линейного программирования (ЗЛП) – задача оптимизации линейной функции при линейных ограничениях.

2. Задача нелинейного программирования (ЗНП) – задача оптимизации нелинейной функции при ограничениях или без них (когда или F(x) и/илиg_i(x) нелинейны).

3. Задача дискретного (в частности целочисленного) программирования – Задача оптимизации, в которой на переменные наложено дополнительное требование принимать лишь дискретные (в частности целочисленные) значения.

4. Задача динамического программирования – задача оптимизации динамических систем (т.е. развивающихся с течением времени).

5. Задача вероятностного или стохастического программирования – задача оптимизации, содержащая случайные величины.

2. Основные понятия теории оптимизации.

Говорят, что функция F(x) имеет в т. х*(х₁,х₂, … , х_n) локальный максимум (минимум), если существует такая окрестность т. х*, в которой для любого х выполняется неравенствоF(x) ≤F(x*) (F(x) ≥F(x*)).

F(x) 1 – точки локального максимума;

1 F_max2 – точки локального минимума.

1

2

2 Точки локального максимума и

локального минимума называют

F_minточками экстремума.

Необходимое условие экстремума: чтобыF(x) имела в т. х* экстремум необходимо, чтобы ∂F(x*)/∂x_j = 0,.

Достаточное условие экстремума:еслиF(x) в т. х* имеет ∂F(x*)/∂x_j = 0,, то чтобы в этой точкеF(x) имела экстремум достаточно, чтобы квадратичная форма

была положительно (минимум) или отрицательно (максимум) определена.

Очевидно, что точки локального экстремума могут не давать наибольшего или наименьшего значений функции в некоторой области, кроме того, их может быть несколько. Большое значение в этой связи приобретает понятие выпуклости множества допустимых значений и выпуклости (вогнутости) функции.

Множество S называется выпуклым, если для любых двух точек этого множества оно содержит и отрезок, соединяющий эти точки:

Функция F(x), определенная на выпуклом множестве S, выпукла, если ее график целиком лежит ниже (не выше) отрезка, соединяющего любые две точки графика:

Функция F(x), определенная на выпуклом множестве S, вогнута, если ее график целиком лежит выше (не ниже) отрезка, соединяющего любые две точки графика:

Теорема 1: пересечение выпуклых множеств является выпуклым множеством.

Теорема 2:сумма выпуклых функций является выпуклой функцией,

сумма вогнутых функций – вогнутой функцией.

Теорема 3 (основное свойство выпуклых задач):

Всякий локальный оптимум является глобальным.

Теорема Вейерштрасса:

Непрерывная функция, определенная на непустом замкнутом

ограниченном множестве, достигает максимума (минимума) по

крайней мере в одной точке этого множества.

Из сказанного можно определить общий принцип решения задач оптимизации: максимум (минимум) F(x) при х, принадлежащих замкнутому допустимому множеству, если оно существует, является либо точкой экстремума, либо граничной точкой допустимого множества, либо и тем и другим одновременно.

При численных расчетах часто необходимо использовать еще два важных понятия.

Вектор, указывающий направление наискорейшего возрастания функции, называется градиентом функции grad F(x) = (∂F/∂x₁, … ,∂F/∂x_n). Противоположный ему вектор называют антиградиентом, он указывает направление наискорейшего убывания функции.

Линией уровня (или линией равного значения) функции F(x) называют геометрическое место точек, координаты которых удовлетворяют уравнению F(x) = Const. Линия уровня и вектор градиент в каждой точке взаимно перпендикулярны.

3. Постановка ЗЛП, различные формы записи. Примеры экономических задач.

Линейное программирование – раздел математического программирования, рассматривающий задачи оптимизации линейных функций многих переменных при линейных ограничениях на область изменения переменных.

Особенностью ЗЛП является то, что линейная целевая функция не имеет экстремума и достигает наибольшего или наименьшего значения на границе допустимой области.

Рассмотрим постановку ЗЛП на примере задачи и наилучшем использовании ресурсов.Имеетсяmвидов ресурсов в ограниченном количествеb= (b₁,b₂, … ,b_m). Ресурсы используются предприятием для выпускаnвидов продукции. Известна экономическая выгода производства каждого вида продукции, исчисляемая, например, ценой реализации С = (С₁, С₂, … , С_n). Известны технологические коэффициенты а_ij, соответствующие количествуi-го вида ресурса, необходимого для производства единицыj–го вида продукции – А = ( а_ij). Необходимо составить план производства х = (х₁,х₂, … , х_n), приносящий предприятию максимальную прибыль.

В общем виде математическую модель задачи (ЗЛП) можно записать следующим образом:

F(x) = C₁x₁ + C₂x₂ + … + C_nx_n → max

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n ≤ b₁, x_j ≥ 0, j=

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n ≤ b₂,

… … … …

a_m1x₁ + a_m2x₂ + … + a_mnx_n ≤ b_m.

Рассмотрим задачу о диете.Необходимо составить диету (рацион), содержащую определенные питательные вещества. Имеемnвидов продуктов, каждый из которых сожержит необходимыеmвидов питательных веществ. Единицаj-го продукта содержит а_ijединицi-го питательного вещества. Для нормальной жизнедеятельности необходимо не менееb_iединицi-го вещества. Известна стоимость единицы каждого вида продукта С = (С₁, С₂, … , С_n). Необходимо составить диету минимальной стоимости.

Математическая модель задачи примет вид:

F(x) = C₁x₁ + C₂x₂ + … + C_nx_n → min

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n ≥ b₁, x_j ≥ 0, j=

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n ≥ b₂,

… … … …

a_m1x₁ + a_m2x₂ + … + a_mnx_n ≥ b_m.

Здесь х_j– количествоj– го продукта в рационе.

В матричной форме общая ЗЛП выглядит так:

F(x) = C^Tx → max (min)

Ax≤ (=,≥)B;x≥ 0.

Кроме того, для записи ЗЛП можно использовать знак суммы:

F(x) = →max(min)

,.

Рассмотрим задачу о размещении заказа.Имеетсяmоднородных групп оборудования, на котором нужно выполнить заказ на выпускnвидов продукции в объемах х*_j,. Мощность оборудования ограничена, например, временем Т_i. Производительность оборудования задана коэффициентами а_ij. Известны коэффициенты затрат С_ij– затратыi– го оборудования на производствоj– го продукта. Построить план х_ijразмещения заказа (загрузки оборудования). Составим математическую модель задачи.

F(x) = →min,x_ij≥ 0,j= ,,

- по мощности - ,,

- по видам продукции, план по которой может быть перевыполнен

,j= ,

- по видам продукции, план по которой должен соответствовать заказу

,j= ,

- по видам продукции, заказ на которую принимается для более полной загрузки

оборудования

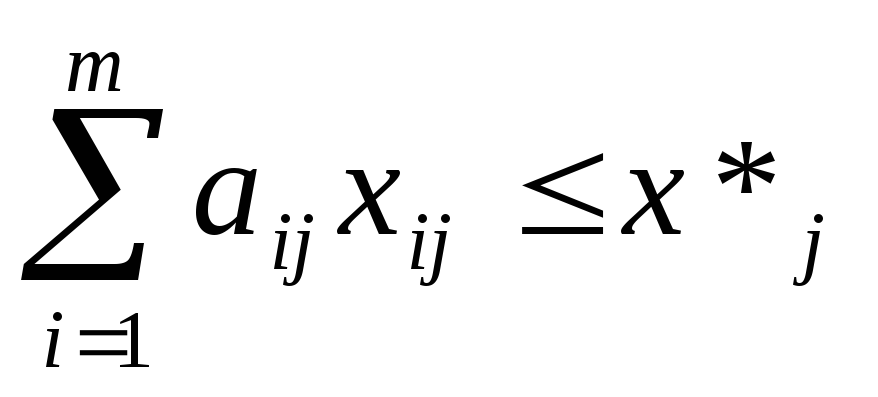,j= .