
Matematika / Модуль 2 / Лекция 6 (Градиентные методы)
.docЛекция 6.
Градиентные методы решения задач нелинейного программирования.
Вопросы: 1. Общая характеристика методов.
2. Метод градиента.
3. Метод наискорейшего спуска.
4. Метод Франка-Фулфа.
5. Метод штрафных функций.
1. Общая характеристика методов.
Градиентные методы представляют собой приближенные (итерационные) методы решения задачи нелинейного программирования и позволяют решить практически любую задачу. Однако при этом определяется локальный экстремум. Поэтому целесообразно применять эти методы для решения задач выпуклого программирования, в которых каждый локальный экстремум является и глобальным. Процесс решения задачи состоит в том, что, начиная с некоторой точки х (начальной), осуществляется последовательный переход в направлении gradF(x), если определяется точка максимума, и –gradF(x) (антиградиента), если определяется точка минимума, до точки, являющейся решением задачи. При этом эта точка может оказаться как внутри области допустимых значений, так и на ее границе.
Градиентные методы можно разделить на два класса (группы). К первой группе относятся методы, в которых все исследуемые точки принадлежат допустимой области. К таким методам относятся: метод градиента, наискорейшего спуска, Франка-Вулфа и др. Ко второй группе относятся методы, в которых исследуемые точки могут и не принадлежать допустимой области. Общим из таких методов является метод штрафных функций. Все методы штрафных функций отличаются друг от друга способом определения «штрафа».
Основным понятием, используемым во всех градиентных методах, является понятие градиента функции, как направления наискорейшего возрастания функции.
При определении решения градиентными методами итерационный процесс продолжается до тех пор, пока:
- либо grad F(x*) = 0, (точное решение);
- либо
![]() (1)
(1)
где
![]() - две последовательные точки,
- две последовательные точки,
![]() -
малое число, характеризующее точность
решения.
-
малое число, характеризующее точность
решения.
2. Метод градиента.
Представим человека, стоящего на склоне оврага, которому необходимо спуститься вниз (на дно). Наиболее естественным, кажется, направление в сторону наибольшей крутизны спуска, т.е. направление (-grad F(x)). Получаемая при этом стратегия, называемая градиентным методом, представляет собой последовательность шагов, каждый из которых содержит две операции:
а) определение направления наибольшей крутизны спуска (подъема);
б) перемещение в выбранном направлении на некоторый шаг.
Правильный выбор шага имеет существенное значение. Чем шаг меньше, тем точнее результат, но больше вычислений. Различные модификации градиентного метода и состоят в использовании различных способов определения шага. Если на каком-либо шаге значение F(x) не уменьшилось, это означает, что точку минимума «проскочили», в этом случае необходимо вернуться к предыдущей точке и уменьшить шаг, например, вдвое.
Схема решения.
1. Определение х0 = (х1,x2,…,xn),
принадлежащей допустимой области
и F(x0).
2. Определение grad F(x0) или –grad F(x0).
3. Выбор шага h.
4. Определение следующей точки по формуле
x(k+1)
= x(k)
![]() h grad F(x(k)),
«+» - если max,
h grad F(x(k)),
«+» - если max,
«-» - если min.
5. Определение F(x(k+1)) и :
- если
![]() ,
решение найдено;
,
решение найдено;
- если нет, то переход к п. 2.
Замечание. Если grad F(x(k)) = 0, то решение будет точным.
Пример. F(x) = -6x1
+ 2x12
– 2x1x2
+ 2x22
![]() min,
min,
x1 + x2
![]() 2, x1
2, x1
![]() 0, x2
0, x2
![]() 0,
0,
![]() = 0,1.
= 0,1.
3. Метод наискорейшего спуска.
В отличие от метода градиента, в котором градиент определяют на каждом шаге, в методе наискорейшего спуска градиент находят в начальной точке и движение в найденном направлении продолжают одинаковыми шагами до тех пор, пока значение функции уменьшается (увеличивается). Если на каком-либо шаге F(x) возросло (уменьшилось), то движение в данном направлении прекращается, последний шаг снимается полностью или наполовину и вычисляется новое значение градиента и новое направление.
Схема решения.
1. Определение х0 = (х1,x2,…,xn),
принадлежащей допустимой области,
и F(x0), k = 0.
2. Определение grad F(x0) или –grad F(x0).
3. Выбор шага h.
4. Определение следующей точки по формуле
x(k+1)
= x(k)
![]() h grad F(x(k)),
«+» - если max,
h grad F(x(k)),
«+» - если max,
«-» - если min.
5. Определение F(x(k+1)) и :
- если
![]() ,
решение найдено;
,
решение найдено;
- если нет:
а) при поиске min: - если F(x(k+1)) < F(x(k)) – переход к п. 4,
- если F(x(k+1)) > F(x(k)) – переход к п. 2;
б) при поиске max: - если F(x(k+1)) > F(x(k)) – переход к п. 4;
- если F(x(k+1)) < F(x(k)) – переход к п. 2.
Замечания: 1. Если grad F(x(k)) = 0, то решение будет точным.
2. Преимуществом метода наискорейшего спуска является его простота и
сокращение расчетов, так как grad F(x) вычисляется не во всех точках, что
важно для задач большой размерности.
3. Недостатком является то, что шаги должны быть малыми, чтобы не
пропустить точку оптимума.
Пример. F(x) = 3x1
– 0,2x12
+ x2 -
0,2x22
![]() max,
max,
x1
+ x2
![]() 7, x1
7, x1
![]() 0,
0,
x1
+ 2x2
![]() 10, x2
10, x2
![]() 0.
0.
4. Метод Франка-Вулфа.
Метод используется для оптимизации нелинейной целевой функции при линейных ограничениях. В окрестности исследуемой точки нелинейная целевая функция заменяется линейной функцией и задача сводится к последовательному решению задач линейного программирования.
Схема решения.
1. Определение х0 = (х1,x2,…,xn), принадлежащей допустимой области, и F(x0), k = 0.
2. Определение grad F(x(k)).
3. Строят функцию
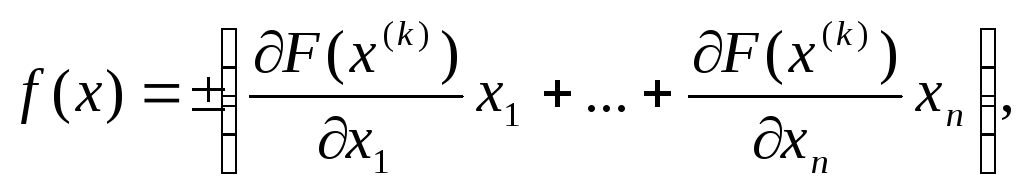 (min – «-»; max – «+»).
(min – «-»; max – «+»).
4. Определение max(min) f(x) при исходных ограничениях. Пусть это будет точка z(k).
5. Определение шага вычислений x(k+1)
= x(k)
+
![]() (k)(z(k)
– x(k)),
где
(k)(z(k)
– x(k)),
где
![]() (k)
– шаг, коэффициент, 0
(k)
– шаг, коэффициент, 0
![]()
![]()
![]() 1.
1.
![]() (k)
выбирается так, чтобы значение функции
F(x) было max (min) в точке х(k+1).
Для этого решают уравнение
(k)
выбирается так, чтобы значение функции
F(x) было max (min) в точке х(k+1).
Для этого решают уравнение
![]() и
выбирают наименьший (наибольший) из
корней, но 0
и
выбирают наименьший (наибольший) из
корней, но 0
![]()
![]()
![]() 1.
1.
6. Определение F(x(k+1)) и проверяют необходимость дальнейших вычислений:
- если
![]() или grad F(x(k+1))
= 0, то решение найдено;
или grad F(x(k+1))
= 0, то решение найдено;
- если нет, то переход к п. 2.
Пример. F(x) = 4x1
+ 10x2
–x12
–x22
![]() max,
max,
x1
+x2
![]() 4, x1
4, x1
![]() 0,
0,
x2
![]() 2, x2
2, x2
![]() 0.
0.
5. Метод штрафных функций.
Пусть необходимо найти F(x1,
x2,…,xn)
![]() max(min),
max(min),
gi
(x1,
x2,…,xn)
![]() bi, i
=
bi, i
=
![]() , xj
, xj
![]() 0, j =
0, j =
![]() .
.
Функции F и gi – выпуклые или вогнутые.
Идея метода штрафных функций заключается в поиске оптимального значения новой целевой функции Q(x) = F(x) + H(x), которая является суммой исходной целевой функции и некоторой функции H(x), определяемой системой ограничений и называемой штрафной функцией. Штрафные функции строят таким образом, чтобы обеспечить либо быстрое возвращение в допустимую область, либо невозможность выходы из нее. Метод штрафных функций сводит задачу на условный экстремум к решению последовательности задач на безусловный экстремум, что проще. Существует множество способов построения штрафной функции. Наиболее часто она имеет вид:
H(x) =
![]() ,
,
где
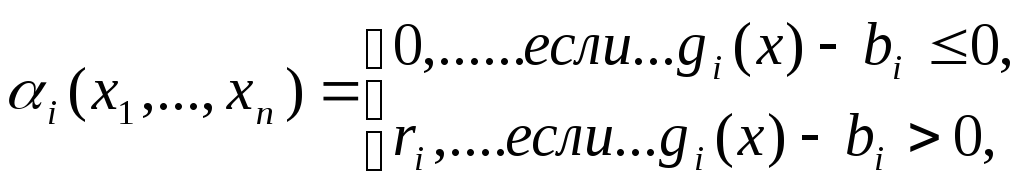
![]() -
некоторые положительные Const.
-
некоторые положительные Const.
Примечание:
- чем меньше
![]() ,
тем быстрее находится решение, однако,
точность снижается;
,
тем быстрее находится решение, однако,
точность снижается;
- начинают решение с малых
![]() и увеличивают их на последующих шагах.
и увеличивают их на последующих шагах.
Используя штрафную функцию, последовательно переходят от одной точки к другой до тех пор, пока не получат приемлемое решение.
Схема решения.
1. Определение начальную точку х0 = (х1,x2,…,xn), F(x0) и k = 0.
2. Выбирают шаг вычислений h.
3. Определяют частные производные
![]() и
и
![]() .
.
4. Определяют координаты следующей точки по формуле:
xj(k+1)
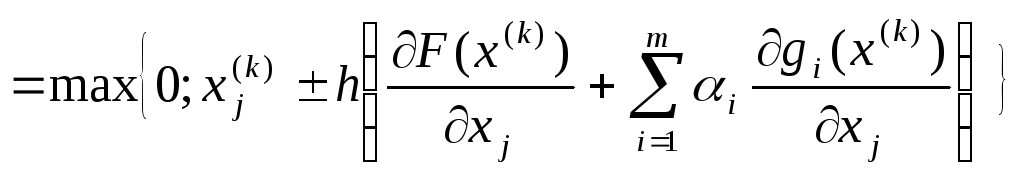 .
.
5. Если x(k+1)
![]() Допустимой
области, проверяют:
Допустимой
области, проверяют:
а) если
![]() -
решение найдено, если нет – переход к
п. 2.
-
решение найдено, если нет – переход к
п. 2.
б) если grad F(x(k+1)) = 0, то найдено точное решение.
Если x(k+1)
![]() Допустимой области, задают новое значение
Допустимой области, задают новое значение
![]() и
переходят к п. 4.
и
переходят к п. 4.
Пример. F(x) = – x12
– x22
![]() max,
max,
(x1
-5)2 + (x2
-5)2
![]() 8, x1
8, x1
![]() 0, x2
0, x2
![]() 0.
0.
