7

1990-2013. Лекция01. Анализ решения фотограмметрической задачи

Цели: выявление промахов, обеспечение точности, оценка точности определяемых величин, топология.

Вопросы лекции

1 Содержание решения

2 Суть анализа решения

3 Норма матрицы

4 Число обусловленности

5 Внешние признаки обусловленности

6 Геометрический смысл числа обусловленности

7 Разное

Лабраб: конкретно оценка всех этапов решения и узора точек сети на стереопаре.

===================================================================

Решение любой фотограмметрической задачи (внутрен., взаимн., внешнее ориент., определение координат точки) идет так:

1. Измеряют. Измерения должны отвечать

(а) общим требованиям:

быть правильными, достаточными, следовать симметричному закону распределения (обычно нормальному);

(б) требованиям частной задачи. (Подробнее рассмотрим эти требования на следующих лекциях.) Сейчас просто запомните, что точность результата, соответствующая точности Ваших прямых измерений, может быть достигнута только тогда, когда Вы выполнили измерения по предписанной технологии. Иначе – точность результата ВСЕГДА будет ниже, хотя вычисленные по этим измерениям значения оценок его точности (СКО) и будут малы.

2. Составляют уравнения связи (1.1) измеренных и искомых величин. К искомым величинам Х относят как непосредственно измеренные величины, так и определяемые (вычисляемые), а также вспомогательные величины Т. Например, геодезические координаты опорной точки измерены, а определяемой – вычислены. Элементы внешнего ориентирования снимка (параметры Т) – вспомогательные величины, как правило, вычисляются.

3. Решают систему уравнений. В фотограмметрии уравнения связи обычно сложные, нелинейные.

Их решают методом приближений Ньютона. Для этого, пользуясь начальными значениями Х и Т, переходят от строгих исходных зависимостей (1.1) к приближенным линейным (1.2)

(здесь: A- матрица частных производных;T – вектор поправок к начальным значениям параметров; - вектор свободных членов, невязок, вызванных неточным знанием значений параметров и погрешностями прямых измерений; а V –вектор расхождений вычисленных и измеренных значений, который называют вектором невязок или вектором поправок к измеренным значениям. Необходимо помнить, что эти «поправки» не уточняют результаты прямых измерений, а только приводят к выполнению условия . (Например, это поправки к реальным показаниям температуры каждого студента, такие, чтобы средняя температура в группе была 36.5 градуса. Причем, если у Ивановой – 37.3, то поправка Петрову -0.8 градуса.) Эти линейные уравнения называют уравнениями поправок.

Необходимое число уравнений k системы равно числу определяемых величин (косвенных измерений). Найденные из решения этой системы значения определяемых величин будут единственными, бесконтрольно определенными, следовательно, недостоверными.

Чтобы решение приобрело какую-то достоверность, необходимо сделать дополнительные измерения. Каждое дополнительное, т.е. избыточное сверх необходимых измерение, дает одно избыточное уравнение . Поэтому при наличии избыточных измерений количество n уравнений в системе (1.2) превышает число k искомых величин на число избыточных измерений r= n - k. Система переопределена. Вследствие погрешностей измерений каждый набор из k уравнений даст свое решение по методу Ньютона. Оно не совпадет с решением из другого набора.

Для того, чтобы использовать все множество решений применяют какое-либо правило нахождения среднего из них. Существует несколько таких правил. Наиболее широко применяют изученное Вами правило м.н.к., ввиду его крайней простоты. По этому правилу получают псевдорешение, т.е. не истинное решение, а такое, которое обеспечивает выполнение правила. Корни этого решения в оптимальном случае лежат в области корней множества решений, полученных изо всех наборов уравнений (но могут оказаться и весьма далеко за пределами этой области).

С точки зрения теории вероятностей это псевдорешение обладает наибольшей плотностью вероятности. Суть правила м.н.к. в том, что ФункцПлотнВер имеет максимум при , ибо показатель степени экспоненты отрицательный. Минимум степени суммы квадратов [pv² ] будет при . Отсюда название: м.н.к.

4. Правило м.н.к. преобразует уравнения поправок в нормальные уравнения . Или короче . В этой преобразованной системе число уравнений равно числу (n-r)=k искомых величин Т. Система нормальных уравнений может иметь единственное решение или не иметь никакого. Поэтому нужно проверить, существует ли решение. Если решение существует, то надо выяснить, какова точность этого решения, и какие причины вызывают падение точности. Именно в этом суть работы инженера: не определять положение точек объекта (это дела техника-оператора), но оценить точность этого определения и выявить причины потери точности.

Формально матрицу нормальных уравнений можно составить по одному только уравнению поправок. Если , то градиент , a для одного измерения есть . Эта система для одной точки вырождена: определитель матрицы тождественно равен нулю. Решения нет. Чтобы получилось решение, надо получить такие матрицы – слайды для ряда точек и сложить их. Таких слайдов д.б. не менее числа искомых величин. Если число уравнений поправок равно числу неизвестных, и уравнения линейно независимы, то решение системы единственное. Однако, любая ошибка измерений (сбой, промах) войдет в это решение бесследно. Заметить ошибку по решению, без дополнительных данных, нельзя.

Если у нас будет одно – два измерения сверх необходимых, то мы составим по ним еще одно - два уравнения. Включив их в систему уравнений и решая ее, иногда можем заметить, что не все в решении ладно. Однако найти ошибку и даже порядок ошибки затруднительно. Поэтому лучше следовать правилу: минимум ТРИ прямых измерения на каждое неизвестное. Как располагать измеряемые точки в плоскости измерений (на снимке) Вы определите из анализа решения в ЛабРаб1.

Теперь перейдем к сути анализа решения.

Решение системы (если оно существует) есть . Для анализа продифференцируем это равенство: . Итак, ошибка решения dT слагается из двух частей.

Первое слагаемое показывает погрешность, вносимую в решение ошибками dL* свободного члена нормальных уравнений . dL* складывается из ошибок измерений и ошибок начальных значений параметров: L=qизм - qвычисл. При решении вектор шибок dL* умножается на N^-1 . Эта матрица по сути есть масштабный коэффициент, который увеличивает исходные ошибки . Нужно оценить, что может сделать эта матрица в худшем случае. (т.е. тогда, когда наибольшие компоненты вектора dL* умножаются на наибольшие члены в N^-1). Для оценки используем понятие “нормы матрицы”. По сути, норма - это максимальный масштаб. При данном векторе ошибок dL*, чем меньше норма, тем меньше увеличиваются ошибки определения неизвестных.

(Сингулярность и пр для А⁺: . удобно: непосредственно зависит от св.чл. делают в ЛабРаб1)

Второе слагаемое показывает погрешность, вносимую в искомое решение ошибками определения коэффициентов матрицы N и ошибками ее обращения для получения N^-1. Оценивают влияние второго слагаемого по значению характеристики “число обусловленности” (condition - условие). При данном L*, чем меньше число обусловленности (кондиция), тем меньше ошибки определения неизвестных, вносимые ошибками коэффициентов.

Рассмотреть

Вспомним понятия нормы и кондиции.

Норма матрицы A . При умножении векторов Х одной и той же длины, но различного направления, на матрицу А длина вектора будет разной.

Характеристика «норма матрицы» показывает максимально возможное увеличение вектора X после умножения его на эту матрицу A: . Длина вектора Y(его модуль, евклидова норма) есть , а вектора X - . Отсюда получают одну из норм матрицы: . Эта норма называется спектральной.

Примечание. Применяют и другие нормы. Например, (1) евклидову норму матрицы, она же - норма Фробениуса (F-норма), она же норма Шура, коя аналогична евклидовой норме вектора; (2) первую, равную модулю максимальной координаты, или (3) бесконечную, равную сумме модулей его координат

Пример 1. Топографическая карта масштаба 1:50000. Геодезические координаты точки х_g, у_g (точнее их приращения относительно некоторой известной точки), как вы знаете, находим так: норма матрицы здесь ||A||=50000. Если карта сделана так, что по одной оси масштаб 1:50000, а по другой - 1:10000, то норма А по определению остается та же ||A||=50000, так как из векторов равной длины мы можем взять такой, что [x=|X| y=0]^Т.

Свойства нормы

Различные виды норм применяют, исходя из простоты их вычисления или особенностей решаемой задачи. Однако любая неотрицательная величина, выбираемая в качестве нормы, должна отвечать условиям суммирования и умножения:.

Рассмотрим одну из важных для нас норм (правда, трудно реализуемую для больших матриц) спектральную норму. Согласно теореме Лагранжа симметричную матрицу N ортогональным преобразованием A (преобразованием поворота, не меняющим длину вектора Y=AX), можно привести к диагональному виду: 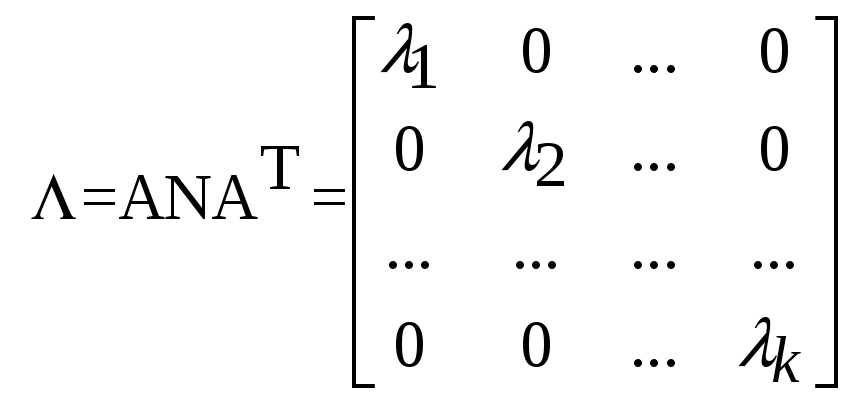. Матрица  будет подобна матрице N, так как выполняется соотношение подобия . Это следует из того, что ортогональная (ортонормированная) А неособенная, так как ее определитель |A|=1(дать пояснения: при обычных скоростях поворот Вашего конспекта не изменяет его размера). Значит для нее существует обратная матрица А^-1 . Так как определитель равен единице, то согласно формуле обращения матриц, эта обратная равна ее транспонированной А^т . Поэтому преобразование есть преобразование подобия (при коэффициенте =1, т.е. тождественно)

Если матрица приведена к диагональному виду, то ее спектральная норма будет: (сферическая= корень квдратный из суммы квадр всех лямбда) так как из множества векторов одной и той же длины можно взять такой, что его х_макс есть сомножитель _max , а другие его компоненты равны нулю.

Вывод: спектральная норма матрицы есть максимальный элемент  на главной диагонали диагональной матрицы .

Коэффициенты _i находят, решая так называемое вековое уравнение . Набор _i называют спектром матрицы. Отсюда и название этой нормы.

Если матрица прямоугольная, то несколько _i будут равны нулю. Это видно из того, что квадратную (прямоугольную) можно превратить в прямоугольную (квадратную), дописав одну или несколько нулевых строк или столбцов;  (μ) называют числами сингулярности, ибо А сингулярная (особая), если |A|=0).

В алгебраической форме вековое уравнение выглядит так: .

Все коэффициенты этого уравнения (суммы главных миноров) являются инвариантами поворота. Следовательно, коэффициент при ⁰ - определитель |N| - инвариант. Поэтому |N|= || , т.е. произведение всех _i есть определитель |N|. Следовательно, если хотя бы одно _j равно нулю, то определитель |N| равен нулю.

Сумму всех _i (главный минор первого порядка) называют след матрицы, Sp(N), Trace(N). Так как след есть коэффициент при ^k-1, т.е. инвариант, то .

Следствие 1. Для положительно определенной матрицы (такова N) норма _max не может превзойти значения следа матрицы. Если же норма равна следу, то все остальные _i суть нули, т.е. матрица особенная.

Следствие 2. След характеризует верхний предел нормы матрицы N.

Следствие 3. Для неособенной матрицы число _min не может быть равно нулю. Для положительно определенной матрицы _min более нуля.

НОРМУ матрицы M, квадратной несимметричной, или прямоугольной (например, вертикальной) находят так. Сначала из M получают симметричную положительно определенную N=M^т M. Для этой N находят _i и норму ||N||. В качестве спектральной нормы для M принимают .

Вывод: Спектральная норма матрицы уравнений поправок в sqrt меньше нормы матрицы нормальных уравнений.

Примечание, если сложно найти , то можно приближенно оценить их пределы на основе принципа Релея

|, .

Примеры других норм. Первая норма - максимальная сумма модулей элементов столбцов (по аналогии с первой нормой вектора = сумме модулей координат)

Вывод: погрешность решения в неблагоприятном случае не превзойдет

Обусловленность

Вторая характеристика называется “Число обусловленности”(Condition –кондиция, condicio – лат. условие) системы линейных уравнений. Она показывает, во сколько раз ошибка определения неизвестных может оказаться больше ошибки определения коэффициентов системы уравнений.

Применяют различные числа обусловленности. Различаются они тем, что их вычисляют по различным нормам матриц. В частности число обусловленности, определенное по спектралной норме (число Тодта?), показывает, во сколько раз относительное СКО искомых величин может быть больше относительного СКО определения коэффициентов. (т.е. с какой относительной точностью надо знать коэффициенты)

Относительное . (уточнить n I Dx=|X|

Найдем число обусловленности . Для этого в избавимся от L* (влияние ошибок которого мы уже рассмотрели). Из исходного равенства следует . Отсюда. И мы видим, что вектор погрешностей параметров зависит от погрешностей обращения матрицы , от матрицы N и от значений параметров T.

Чтобы численно оценить, что мы можем ожидать при наиболее неблагоприятном направлении вектора T при данной N, (чтобы работать с числами), перейдем от матриц и векторов к их нормам: , где , т.е. это СКО t , умноженное на корень квадратный из числа компонент вектора.

Теперь можем получить относительное СКО искомого вектора Т, разделив обе части этого равенства на неравный нулю модуль |T|. (Если |T|=0, то и |dT_N |=0.)

Учитывая свойство нормы произведения, получаем, что относительное СКО (умноженное на sqrt(k)) определения вектора Т не превосходит .

Перейдем к относительным СКО определения коэффициентов матрицы N^-1. Для этого умножим справа это выражение на. Получаем относительное СКО коэффициентов (без деления на sqrt(k) , можно и разделить на sqrt(k), но нет нужды), умноженное на коэффициент:

.

Вот этот коэффициент и называют числом обусловленности .

Выразим через спектральные нормы.

Норма || N|| = _maxN, а норма ||N^-1||= _maxN -₁. Так как, а , то _maxN-₁ =_minN . Отсюда число обусловленности _.

При все  одинаковы, т.е ,  скалярна. Поэтому можно представить  как произведение коэффициента  на единичную матрицу Е. Умножение на такую матрицу  есть приведение к новому масштабу, умножение на скаляр. Относительная точность результата, обусловленная решением, будет та же, что и относительная точность коэффициентов матрицы N, т.е. точность задания масштаба. Так обусловленность любой топографической карты равна единице. Полагают, что масштаб точно соответствует указанному на карте. Поэтому точность определения координат определяется точностью измерения координат на карте.

При относительная точность результата может оказаться в наиболее неблагоприятном случае в это же число раз хуже относительной точности коэффициентов. Такая система считается хорошо обусловленной, так как достаточно двух - четырех верных цифр в коэффициенте (число нулей), чтобы получить одну верную цифру в решении.

При порядка миллионов систему считают плохо обусловленной. При решении такой системы крайне незначительные изменения коэффициентов (например, один из коэффициентов изменится на 0.0000000001) приведут к совершенно другим корням уравнения, т.е. к неправдоподобному решению.

Примечание. В качестве числа обусловленности можно было бы взять величину, обратную , т.е. . Такая характеристика наглядно показывала бы, что при плохой обусловленности выполняется деление на число, близкое к нулю.