10

Ревизия .2003,04,06,15_10_0715_09_09.

Лекция02 О решении систем нормальных уравнений

Содержание

1. Обращение блочной матрицы

2. Решение системы рекурсивным разделением на блоки

3. Решение систем рекуррентным способом

4. Решение слабо обусловленных систем

ПРИЛОЖЕНИЕ 1. Один снимок

ПРИЛОЖЕНИЕ 2. Пара снимков

Основные способы решения систем нормальных уравнений (СНУ) вы изучили (Гаусса, кв. корней, приближения и т.д.). Вы помните, что нормальные уравнения - это частный случай системы линейных уравнений (СЛУ) с симметрической матрицей коэффициентов.

Мы коснемся только больших СЛУ (систем линейных уравнений).

Рисунок Портрет матрицы нормальных уравнений маршрута фототриангуляции. Матрица содержит 4 блока: два квадратных диагональных симметрических: ЭВОС (синие) и XYZ точек (красные) и два блока связи этих диагональных: первый и второй =транспонированный первый блок. Незакрашенные подблоки содержат нули

	ЭВОС1	ЭВОС2	…	ЭВОСм	XYZ1	XYZ2	XYZ3	XYZ4	…	XYZ7	XYZn
1	6x6				6х3
2		6x6
///			6x6
m				6x6
XYZ1	3х6				3x3
XYZ2						3x3
XYZ3							3x3
XYZ4								3x3
…									,,,,,
XYZ7										3x3
XYZn											3x3

Использование различных дополнительных данных и условий приводит к заполнению некоторых из этих нулевых подблоков в диагональных квадратных блоках (ЭВОС и ХУZ), что усложняет решение.

Система НУ в фотограмметрии резко возрастает, когда наряду с параметрами вычисляют еще и поправки к измеренным величинам. Прямое решение такой НУ затруднительно: занимает много памяти ЭВМ, требует множества обращений к ВЗУ, множество операций с нулями, необходимость хранения нулей и чисел с большим числом разрядов во избежание потери точности при округлении и др..

Если требуется полная характеристика точности всех определяемых величин, то решение получается еще более сложным, ибо необходимо обращать матрицу N. Такая полная характеристика, а именно ковариационные матрицы параметров и вектора измеренных величин, необходима тогда, когда нужно оценить точность функций параметров и измеренных величин. Так как все наши фотограмметрические определения: элементы ориентирования снимков, координаты точек местности суть такие функции, то нахождение таких матриц обязательно. Чтобы облегчить решение, применяют разные подходы к обращению матрицы. Покажем из них три подхода.

1. Обращение блочной матрицы. Суть в том, что большую матрицу разбивают на 4 блока (подматрицы), с которыми действуют почти так же как с числами.

Рассмотрим решение на примере разбития матрицы на ЧЕТЫРЕ блока. При необходимости каждый блок главной диагонали в свою очередь можно разбить на четыре подблока и применить то же решение и т.д.

При разбиении руководствуются следующим:

вдоль главной диагонали выделяют квадратные блоки; делают так потому, что для неособенной матрицы (определитель не равен нулю) любые блоки, главная диагональ которых совпадает с гл. диагональю этой матрицы также неособенны, т.е. имеют обратную матрицу;

вне главной диагонали стараются выделить нулевые блоки; эти блоки могут быть прямоугольными, а ненулевые квадратные - не иметь обратной матрицы: . Приведем решение для общего случая несимметричной матрицы. Пусть N имеет обратную матрицу .

По определению обратной матрицы NM = MN = E, где Е единичная матрица. Сделав блочное умножение и приравняв матрицы, получаем . Откуда - четыре уравнения с 4 неизвестными блоками М_ii .

При нахождении неизвестных матриц М_iij должны помнить, что обратную имеют только блоки на главной диагонали (N₁₁, N₂₂)

1 Из (3), умножая слева на , находим .

2 Найдем. Для этого подставим в уравнение (1):

и, умножая слева на обратную , получаем .

3 Из равенства (2) находим: . Подставляем его в (4) и получаем :

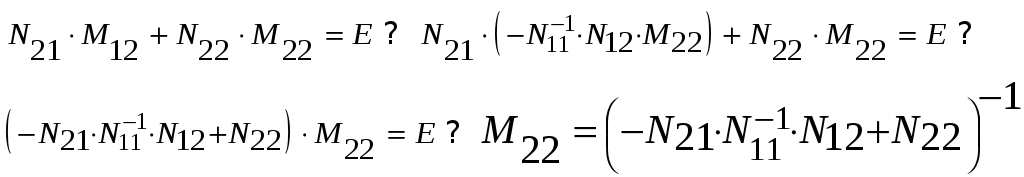
4 Возвращаясь к пункту 3, подставляем , плучаем .

Примечания

1 Матрица системы нормальных уравнений симметрическая. Поэтому , и п.4 не нужен, а находим непосредственно из (4) : .

2 Если вне диагональный блок , то решение распадается на два независимых:

3 Если блоки большие, то к ним при нулевых внедиагональных блоках можно применить тот же подход. Но! С ненулевыми внедиагональными блоками в общем случае (а решение в алгоритмах всегда разрабатывается для общего случая) этого делать нельзя

4 Если расположение точек при взаимном и др. ориентировании нестандартно, то не будет нулевых блоков, блоки будут заполнены. Это приводит к усложнению решения, к ухудшению обусловленности системы и к усложнению определения собственных чисел матрицы.

5 Рассмотренную процедуру в свою очередь можно применить еще много раз для обращения каждого из квадратных блоков главной псевдодиагонали, т.е делим на четыре и делим на четыре . Новые диагональные в свою очередь также можем делить. В нашем случае подблоки 3х3 и 6х6 невелики, но, когда существуют дополнительные связи, и блоки имеют ненулевые боковые блоки, то подобное разбиение эффективно.

Пример. (См. ПРИЛОЖЕНИЕ 1.Сеть из одного снимка). Система нормальных уравнений фотограмметрической сети это квадратная система, которая очевидно из портрета матрицы разделяется на четыре блока. На главной псевдодиагонали один блок N₁₁ содержит псевдодиагональ квадратных подблоков размера 6х6 определяющих ЭВОС снимков сети (вектор T). Второй блок N₂₂ содержит псевдодиагональ квадратных подблоков размера 3х3, определяющих геодезические координаты опорных и связующих точек (вектор R) Все эти подблоки – положительно определенные матрицы. Третий N₁₂ и симметричный ему четвертый N₂₁ блоки содержат псевдодиагонали связи ЭВОС с точками (вставить табличку из Excel).

Пусть система уравнений поправок фотограмметрической сети, где Т-вектор параметров, R– вектор координат L вектор невязок, а V вектор поправок. Обратная ковариационная матрица K^-1 (или матрица весов P=E). Переходя к псевдорешению по м.н.к., получаем систему нормальных уравнений .

Симметрическая матрица N содержит четыре очевидных блока.Эта БОЛЬШАЯ система в блоках выглядит так

. Приняв обозначения , перепишем систему в виде двух равенств .

Из второго равенства найдем вектор

и подставим его в первое: .

Отсюда получаем ..

Чтобы дважды не вычислять одно и тоже, преобразуем

(так как ) и .

Обозначив общую часть , получим параметры .

Обращение присутствующей во всех этих равенствах псевдодиагональной матрицы N₂₂, состоящей из n блоков 3х3 (где n число точек), не вызывает затруднений. Матрица (WA) коэффициентов редуцированной системы нормальных уравнений (размером k*k) намного меньше N₂₂ ((k+n)*(k+n)). Поэтому решение намного упрощается. Выполнив по этой редуцированной системе ряд приближений (согласно методу Ньютона), находим параметры T. По ним уточняем коэффициенты в A и B. Из второй системы получим поправки к координатам , дисперсию единицы веса и ковариационные матрицы, если они нужны.