12

Лекция МО7 fnc Оценки функции измеренных величин (из главы 9)

Содержание

Оценка функции случайного вектора Линейная функция Нелинейная функция

Техника нахождения оценки

Вектор-функция случайного вектора

Вычисление значения оценки

9.3. Вес функции измеренных величин

9.3.А Измеренные величины некоррелированы

9.3.Б Измеренные величины коррелированны

9.4. Определение доверительного интервала для математического ожидания, дисперсии и стандарта функции случайного вектора

Доверительный интервал математического ожидания функции

Доверительный интервал дисперсии (стандарта) функции

9.5. Допуски для функций

Допуски для явных функций

Допуски для невязок

Оценка результатов наблюдений

9.5. А. Обработка равноточных измерений

Нахождение результата. Оценка точности результата. Дисперсия и СКО (стандарт) среднего

Нахождение оценок других характеристик точности результата измерений

9. 5. Б Обработка прямых неравноточных измерений

Нахождение результата х неравноточных некоррелированных измерений. Функция правдоподобия для нормального распределения

Оценка точности результата неравноточных некоррелированных измерений

9.5.В Обработка неравноточных коррелированных измерений

Нахождение результата х неравноточных некоррелированных измерений.

Оценка точности результата неравноточных коррелированных измерений

=======текст=====

Оценка функции случайного вектора

В производственных работах мы выполняем постоянно две процедуры: находим значения функций случайного вектора прямых измерений (ЭВОС, координаты точек, горизонталь и т.д.) и оцениваем точность определения найденных значений этих функций. При отработке технологии дополнительно оцениваем их правильность (нормальность).

Случайный вектор характеризуется математическим ожиданием вектора и ковариационной матрицей. Случайные величиныXi следуют неким распределениям.

Зная ковариационную матрицу вектора случайных, в частности измеренных, величин Kx и его МО{X}, можем оценить функцию этого вектора в точке. Так длянормальных распределений достаточно найти следующую групповую оценку функции : математическое ожидание МО{Y} и дисперсию ²_y.

(При других распределениях набор оценок функции может быть другим.)

Еслина оцениваем интервале нелинейна, то по методу моментов можно найти математическое ожидание (МО) функции на этом интервале

и дисперсию функции на этом интервале , Но это возможно только тогда, когда распределения (X), да и сама функция f(X) на оцениваем интервале, таковы, что интеграл Стилтьеса берется!

Дать рисунок.

Линейная функция. Нахождение оценок упрощается, если функция линейна, т.е., векторX нормален , и известны вектор математических ожиданий X_ср и ковариационная матрица этого вектора Kx. Оценка среднего функции: и дисперсии .(здесь и ниже М или МО – знак математического ожидания).

Первая формула очевидна. Выведем формулу оценки :

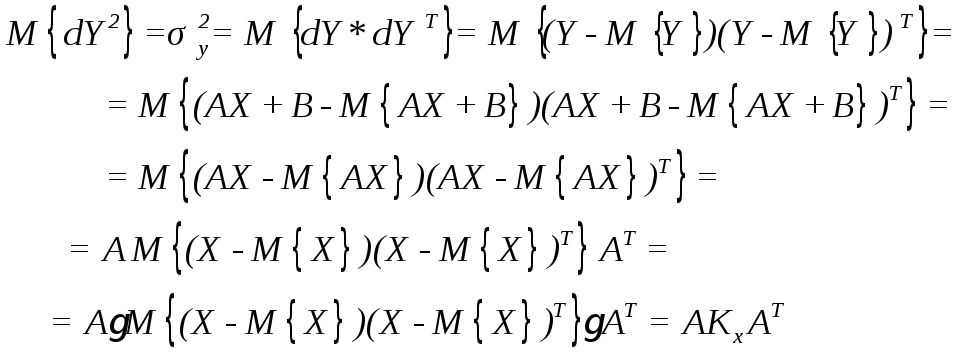(9.1)

Эти оценки будут правдоподобны, если все компоненты вектора не противоречат нормальным распределениям.

Нелинейная функция. Этот подход применим и к нелинейной функции в тех условиях, когда эту функцию на оцениваемом интервале допустимо рассматривать как линейную. Поступаем так. Находим вектор-строку значений частных производных в точке :. Далее для краткости вектор-строку частных производных будем называть без особой натяжки градиентом, так как мы подразумеваем, что дифференциалы аргументов, а равно и производные умножены на соответствующие орты (i,j,k,…).

Мы получили функцию, линейную в точке . Значит все, что сделали выше, будет верно и здесь при условии, что на интервале функция линейна. Поэтому достаточно заменить в (9.1) строку коэффициентовA строкой F значений частных производных в точке : .(Коэффициент B =0 в линеаризованной функции , как производная от постоянной величины).

Вынося градиент F за знак математического ожидания , (ибо F =[f/x₁,... f/x_n]_Xср. это вектор-строка значений производных в точке Хср, т.е. вектор постоянных величин} приходим к выражению, аналогичному (9.1),

(9.2)

где x диагональная матрица, на главной диагонали которой стоят оценки S_i стандартов X_i (СКО), 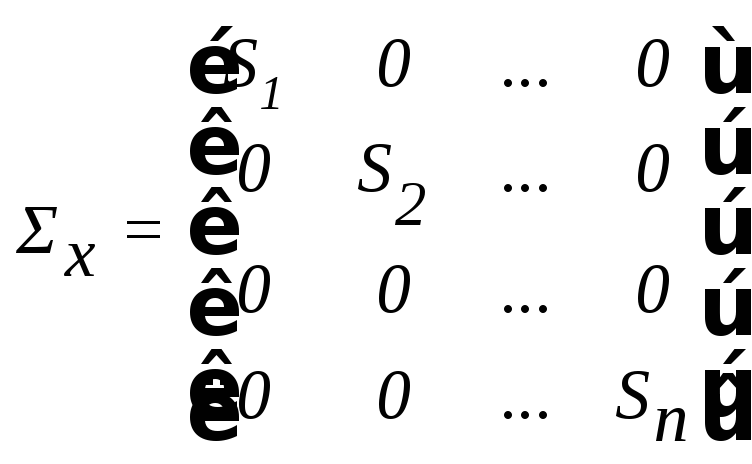, а R_X – корреляционная матрица вектора X. (9.3)

Существенное отличие (9.2) от (9.1) в том, что по(9.2) правильные оценки найдем лишь тогда, когда функция на оцениваемом участке линейна. Если в пределах значения производных изменяются настолько, что они приведут к изменению ²_y более, чем на 10 -20%, то оценка S²_y, зачастую будет смещенной.

Эти оценки будут правдоподобны лишь тогда, когда распределения всех компонент вектора X не противоречат нормальным распределениям.