Лекции / Теория электромагнитного поля_каз / Лекция 11

Дәріс 11.

Тақырыбы: Релятивистік механикадағы гравитациялық өріс.

Дәріс жоспары:

1. Галилейдің координаттар жүйесі.

2. Гравитациялық өрістегі бөлшектің қозғалысы.

Дәріс мәтіні:

Гравитациялық өрістердің негізгі қасиеті (оларда барлық денелер бірдей қозғалады) релятивистік механикада да орын алады. Бұнда да гравитациялық өрістер мен санақтың инерциалды емес жүйелері арасында аналогия орынды. Сондықтан релятивистік механикада гравитациялық өрістердің қасиеттерін зерттеген кезде бұл аналогияны қолдануға болады.

Санақтың инерциалды емес жүйесіндегі координаталардың декарттық жүйесінде интервалы болады. Санақтың кез-келген басқа инерциалды жүйесіне өткен кезде (яғни Лоренцтің түрлендіруі кезінде) интервал өз түрін сақтап қалады. Бірақ біз санақтың басқа инерциалды емес жүйесіне көшсек, онда интервалы төрт координаталар дифференциалдарының квадраттарының қосындысы бола алмайды. Сол сияқты бірқалыпты айналатын координаталар жүйесіне көшкен кезде.

(Ω –z осі бойымен айналудың бұрыштық жылдамдығы), интервал келесі түрге ие

.

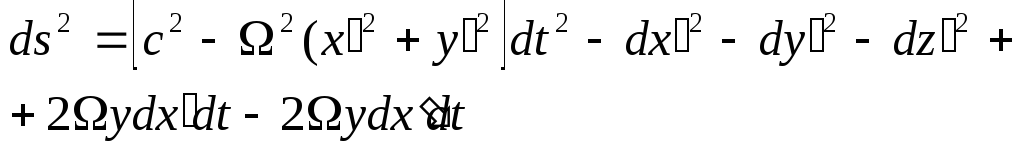Сонымен санақтың инерциалды емес жүйесінде интервал квадраты координаттар дифференциалдарынан шыққан жалпы түрдің кейбір квадраттық формасы, яғни келесі түрге ие

, (124)

мұндағы . Төртөлшемді координаталар жүйесі санақтың инерциалды емес жүйелерін қолданғанда қисық сызықты болып табылады. Координаталардың әрбір берілген қисық сызықты жүйесінде геометрияның барлық қасиеттерін анықтайтын шамалары кеңістік-уақыт метрикасын орнықтырады. шамалары i мен индекстері бойынша симметриялы деп санауға болады. Жалпы жағдайда -ның 10 алуан түрлі шамалары бар. Төртеуінің индекстері бірдей, қалған алтауынікі әр түрлі. Санақтың инерциалды жүйесінде мен декарттық кеңістіктік координаларын пайдалану кезінде шамалары мынаған тең:

, егер . (125)

Бұндай координаталар жүйесі Галилейдік деп аталады.

Санақтың инерциалды емес жүйелері кейбір күштік өрістерге эквивалентті. Релятивистік механикада бұл өрістер шамаларымен анықталады_.. Кез-келген гравитациялық өріс кеңістік-уақыт метрикасының өзгерісі болып табылады, осыған сәйкес шамаларымен анықталады. Бұл кеңістік-уақыттың геометриялық қасиеттері (оынң метрикасы) физикалық құбылыстармен емес, ал кеңістік пен уақыттың өзгермейтін қасиеттерімен анықталатындығын көрсетеді. Реалды кеңістікте анықтауышы әрқашанда g<0.

Салыстырмалы теориясының негізінде құрылған гравитациалық өрістердің теориясы салыстырмалылықтың жалпы теориясы деген атқа ие. Ол Эйнштейнмен құрылған болатын (1915г).

Гравитациялық өрістегі бөлшек қозғалысы

АСТ-тағы еркін материалдық бөлшектің қозғалысы аз әсер ету принципімен анықталады.

. (126)

Бұл принципке сәйкес бөлшек оның әлемдік сызығы екі берілген әлемдік нүктелері арасында эстремальді болатындай етіп қозғалады.

Берілген жағдай үшін ол түзу.

Гравитациялық өрістегі бөлшектің қозғалысы (126) формадағы аз әсер ету принципімен де анықталуы тиіс. Себебі гравитациялық өріс тек -тың арқылы өткендегі өзгерістерде байқалатын кеңістік-уақыт метрикасының өзгерісі болып табылады. Сонымен гравитациялық өрістерде бөлшек оның әлемдік нүктесі 4 өлшемді , , , кеңістікте экстремаль немесе геодезиялық сызығы бойынша орын ауыстыратындай етіп қозғалады. Кеңістік–уақыттың гравитациялық өрісі галилейдік емес болғандықтан, онда бұл сызық түзу емес, ал бөлшектің реалды кеңістіктік қозғалысы- бірқалыпсыз және де түзусызықсыз.

Аз ету принципін пайдаланудың орнына, салыстырмалылықтың арнайы теориясындағы бөлшектің еркін қозғалыстың дифференциалдық теңдеулерін сәйкесті жалпылау жолымен гравитациялық өрістегі бөлшек қозғалысының теңдеулерін жазу ыңғайлырақ, яғни координалардың галилейлік 4-жүйесінде. Бұл теңдеулер , немесе , мұндағы 4-жылдамдық. Қисықсызықсыз координаталарда бұл теңдеу

. (127)

Вектордың ковариантты дифференциалы үшін бұл өрнектен келесіні аламыз:

.

Бұл теңдеулерді ds-ке бөлсек, аламыз:

. (128)

Бұл теңдеулер қозғалыстың теңдеулері. Гравитациялық өрістердегі бөлшектің қозғалысы шамаларымен анықталады. туындысы бөлшектің 4-удеуі. Сондықтан біз шамасын – гравитациялық өрістегі бөлшекке әсер ететін 4-күш деп санауымызға болады. тензоры гравитациялық өрістің потенциалдардың ролін атқарады – оның туындылары өрістің кернеулігін анықтайды. шамаларын байланыстырушы коэффициенттері немесе Кристоффелдің символдары деп атайды.

керісінше

.

Алдыңғы параграфта координаталар жүйесін сәйкесті таңдау арқылы барлық -рды кеңістік-уақыттың кез-келген нүктесінде нольге айналдыруға болады. Санақтың бұндай локальді-инерциалды жүйесін таңдау кеңістік-уақыттың берілген шексіз кіші элементінде гравитациялық өрістің жоқ болуын білдіреді.

Гравитациялық өрістегі бөлшектің 4-импульсі келесідей анықталады:

, (129)

Ал оның квадраты

. (130)

орнына қойсақ, гравитациялық өрістегі бөлшек үшін Гамильтон-Якоби теңдеулерін аламыз.

. (131)

Жарық дабылы таралу үшін (128) формадағы геодезиялық сызық теңдеуін қоладануға болмайды, себебі жарық сәулесі таралудың әлемдік сызығы бойында интервалы мен (128) теңдеудегі барлық мүшелер шексіздіккке айналады. Бұл жағдайда қозғалыс теңдеулерін жазу үшін толқындық векторды пайдаланайық. Оны бізге келесі түрде жазуға болады: k ⁱ = , – сәуле параметрі. АСТ-та бостықта жарықтың таралуы кезінде толқындық вектор сәуле бойында өзгермейді, , яғни . Гравитациялық өрісте бұл теңдеу келесі түрге өтеді: , немесе

(132)

(бұл теңдеулерден λ анықталады).

Толқындық 4- вектордың квадраты нольге тең

. (133)

орнына -ны қойсақ (ψ – эйконал), гравитациялық өрістегі эйконалдың теңдеуін аламыз

. (134)

Кіші жылдамдықтардың шекті жағдайында бөлшек қозғалысының релятивистік теңдеулері сәйкесті релятивистік емес теңдеулерге өту керек. Кіші жылдамдықтар шартынан гравитациялық өрістің әлсіз болатындығын ескеру қажет. Кері жағдайда онда бөлшек үлкен жылдамдықтарға ие болатын еді. Бұндай шекті жағдайда метрикалық тензоры гравитациялық өрістің релятивистік емес потенциалымен тығыз байланысты. Релятивистік емес механикада гравитациялық өрістегі бөлшектің қозғалысы Лагранж формуласымен анықталады. Біз оны келесі түрде жазамыз:

, (135)

-mc² қоссақ, онда гравитациялық өрістегі бөлшек үшін S релятивистік емес әсер келесі түрге ие.

.

Бұл өрнекті келесімен салыстырсақ

,

Біз қарастырылатын шекті жағдайында

.

екендігін көреміз.

Мүшелерді квадраттап, кезінде мүшелердің нольге айналатынын ескерсек,

, (136)

мұнда екені ескерілген. Сонымен, шекті жағдайда метрикалық тензордың компонентасы

. (137)

(136) –дан шығады , . Шынында да оларға қойылатын түзетулер түзетудің реттілігімен бірдей.

Әдебиеттер:

1. Джексон Дж. Классическая электродинамика. М.: Физматгиз, 1962.

2. Новожилов Ю.В., Яппа Ю.А. Электродинамика. М.: Физматгиз, 1978. .

3. Смайт В. Электростатика и электродинамика. М.: ИЛ, 1954.

4. Фейнман Р., Лейторн Р., Сэндс М. Фейнмановские лекции по физике. М.: Мир, 1967. Т. 4,5.