Mtduksi8

Федеральное агентство по образованию Восточно-Сибирский государственный технологический государственный университет

ВВЕДЕНИЕ В ТЕОРИЮ НЕЧЕТКИХ МНОЖЕСТВ

Учебное пособие

Часть I

Издательство ВСГТУ

Улан-Удэ 2004

УДК 519.5 510.22 ББК 22.12

Ха199

Хаптахаева Н.Б., Дамбаева С.В., Аюшеева Н.Н. Введение в теорию нечетких множеств: Учебное пособие. – Часть I. – Улан-Удэ: Изд-во ВСГТУ, 2004. - 68 с.: ил.

Ха199

ISBN 5-89230-199-0

Рецензенты:

Д.Ш. Ширапов, д.ф-м.н., профессор, заведующий кафедрой «Электронновычислительные системы» ВСГТУ Б.М. Степанов, к.т.н., доцент, заведующий кафедрой «Информационные технологии) БГУ

Учебное пособие предназначено для студентов специальностей 220400 «Программное обеспечение вычислительной техники и автоматизированных систем» и 351500 «Математическое обеспечение и администрирование информационных систем». Пособие состоит из двух частей и содержит теоретические основы и приложения по дисциплине «Нечеткая логика». В части I рассмотрены основы теории нечетких множеств: понятие нечетких множеств, нечетких отношений, а также понятие нечеткой и лингвистической переменных. Материал снабжен контрольными вопросами и упражнениями для самостоятельного выполнения.

Ключевые слова: нечёткое множество, нечеткое отношение, нечеткая переменная, лингвистическая переменная, нечеткий логический вывод.

Печатается по решению редакционно-издательского совета Восточно-Сибирского государственного технологического университета.

ISBN 5-89230-199-0	ББК 22.12
	Хаптахаева Н.Б. с соавт., 2004 г.
	ВСГТУ, 2004 г.

2

Оглавление
Введение .............................................................................................................................................	4
1. Нечеткие множества......................................................................................................................	6
1.1. Основные характеристики нечетких множеств...................................................................	6
1.2. Методы построения функции принадлежности.................................................................	10
1.3. Операции над нечеткими множествами .............................................................................	13
1.3.1. Логические операции над нечеткими множествами..................................................	13
1.3.2. Алгебраические операции над нечеткими множествами...........................................	17
Контрольные вопросы.................................................................................................................	21
Упражнения..................................................................................................................................	22
2. Нечеткие отношения и операции над ними...............................................................................	24
2.1. Нечеткие отношения.............................................................................................................	25
2.2. Операции над нечеткими отношениями.............................................................................	28
2.3. Свойства нечетких отношений............................................................................................	33
2.4. Транзитивное замыкание нечеткого бинарного отношения.............................................	37
2.5. Специальные типы нечетких отношений...........................................................................	39
2.5.1. Нечеткие отношения предпорядка...............................................................................	39
2.5.2. Нечеткие отношения порядка.......................................................................................	40
2.5.3. Отношение подобия.......................................................................................................	41
2.5.4. Отношения различия. ....................................................................................................	43
2.5.5. Отношения сходства и несходства...............................................................................	44
Контрольные вопросы.................................................................................................................	46
Упражнения..................................................................................................................................	47
3. Нечеткая и лингвистическая переменные.................................................................................	50
3.1. Понятие нечеткой и лингвистической переменных..........................................................	50
3.1.1. Характеристики простых отношений между нечеткими переменными ..................	52
3.2. Нечеткие числа......................................................................................................................	54
3.2.1. Операции над нечеткими числами...............................................................................	54
3.2.2. Сравнение нечетких чисел............................................................................................	56
3.3. Лингвистические неопределенности...................................................................................	59
3.3.1. Вычисление значений лингвистических переменных................................................	61
Контрольные вопросы.................................................................................................................	64
Упражнения..................................................................................................................................	65
Заключение.......................................................................................................................................	66
Список рекомендуемой литературы ..............................................................................................	67

3

Введение

Наиболее поразительным свойством человеческого интеллекта является способность принимать правильные решения в обстановке неполной и нечеткой информации. Традиционные компьютерные вычисления «слишком точны» для реального мира. Человечество столкнулось с проблемами, для решения которых невозможно получить полную информацию или определение которых недостаточно полно. Казалось бы ситуация безвыходная, но благодаря развитию и совершенствованию так называемых нечетких и гибридных систем в настоящее время уже довольно обыденно воспринимаются «сверхинтеллектуальные» стиральные машины и бытовые автоматы, гиперзвуковые самолеты и самонаводящиеся ракеты и многое другое.

Математическую основу нечетких и гибридных систем составляют противоположные традиционным компьютерным вычислениям (hard computing), так называемые мягкие вычисления (soft computing), одной из составляющих которых является нечеткая логика.

Математическая теория нечетких множеств, предложенная в 1965 в работах Лотфи А. Задэ (Lotfi A. Zadeh), профессора технических наук Калифорнийского университета в Беркли, позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы. Основанные на этой теории методы построения компьютерных нечетких систем существенно расширяют области применения компьютеров. В последнее время нечеткое управление является одной из самых активных и результативных областей исследований применения теории нечетких множеств. Нечеткое управление оказывается особенно полезным, когда технологические процессы являются слишком сложными для анализа с помощью общепринятых количественных методов, или когда доступные источники информации интерпретируются качественно, неточно или неопределенно. Экспериментально показано, что нечеткое управление дает лучшие результаты, по сравнению с получаемыми при общепринятых

4

алгоритмах управления. Нечеткие методы помогают управлять домной и прокатным станом, автомобилем и поездом, распознавать речь и изображения, проектировать роботов, обладающих осязанием и зрением. Нечеткая логика, на которой основано нечеткое управление, ближе по духу к человеческому мышлению и естественным языкам, чем традиционные логические системы. Нечеткая логика, в основном, обеспечивает эффективные средства отображения неопределенностей и неточностей реального мира. Наличие математических средств отражения нечеткости исходной информации позволяет построить модель, адекватную реальности.

Учебное пособие состоит из двух частей и содержит теоретические основы нечеткой логики. Первая часть пособия посвящена математической теории нечетких множеств и состоит из трех разделов.

Впервом разделе рассмотрены основные определения и понятия теории нечетких множеств: характеристики нечетких множеств, методы построения функций принадлежности элемента нечеткому множеству, операции над нечеткими множествами, свойства операций.

Второй раздел содержит основные определения и понятия нечетких отношений и операций над ними, свойств нечетких отношений. Рассмотрены специальные типы бинарных нечетких отношений: нечеткое отношение предпорядка, нечеткое отношение порядка, нечеткое отношение подобия, нечеткое отношение сходства, нечеткое отношение различия.

Втретьем разделе вводятся понятия нечеткой и лингвистической переменных, в качестве значений которых выступают нечеткие множества, а также рассматриваются понятия нечетких чисел и лингвистических неопределенностей.

Каждый раздел сопровождается контрольными вопросами и упражнениями для самостоятельного выполнения.

5

1. Нечеткие множества

1.1. Основные характеристики нечетких множеств

Опр.1.1. Нечетким множеством А во множестве U называется совокупность пар вида (u, µА(u)), где u U, а µА(u)) – это функция принадлежности нечеткого множества А, µА: U → [0,1]. Здесь U – некоторое обычное множество, называемое универсальным множеством.

Для любого элемента U функция принадлежности µА определяет степень принадлежности данного элемента множеству А.

Нечеткое множество можно записать следующим образом:

A = Υ	µA (u) / u
u U	(1.1)

Примеры записи нечетких множеств

1.Если U = (a, b, c, d, e, f); M = (0, 0.5, 1), тогда А можно представить в виде: А = (0/а, 1/b, 0.5/c, 0/d, 0.5/e, 0/f).

2.Если А = (0.8/а1, 1/a2, 0.4/a3, 0.2/a4, 0.5/a5, 0/a6), то U = (a1, а2, а3, а4, а5, а6); M = (0, 0.2, 0.4, 0.5, 0.8, 1).

3.Если элементы множества U являются числовыми значениями, то порядок следования элементов пары должен соответствовать (1.1). U = (1, 2, 3, 4, 5, 6); M = (0, 0.5, 1), тогда А = (0/1, 0/2, 0.5/3, 0.5/4, 0.5/5, 1/6).

Обычные множества составляют подкласс класса нечетких множеств.

Функцией принадлежности обычного множества В U является функция:

1, u B	(1.2)
µB (u) =
0, u B

Опр.1.2. Нечеткое множество А называется пустым, если µA (u) = 0, u U

Опр.1.3. Носителем нечеткого множества А называется обычное подмножество таких точек U, для которых величина µА(u) положительна. Носитель обозначается S(A) или SuppA:

S(A) ={u		u U , µA (u) > 0}	(1.3)

6

Опр. 1.4. Высотой h(A) нечеткого множества А называется величина

h(A) = sup µA (u)	(1.4)
u U

Нечеткое множество А называется нормальным, если его высота равна единице. В противном случае нечеткое множество А субнормально. Отметим, что субнормальное нечеткое множество всегда можно нормализовать, поделив

функцию принадлежности µА на величину h(A) = sup µA (u) .

u U

Опр. 1.5. Элементы множества U, для которых степень принадлежности

µА(u) = 0.5 называются точками перехода нечеткого множества А.

Примеры нечетких множеств

1. Пусть универсальное множество U представлено в виде {a, b, c, d, e} и нечеткое подмножество А, заданное на U, имеет вид A = (0/a, 0.5/b, 0.6/c, 0.7/d, 0.85/e).

Тогда носителем нечеткого множества A является S(A) = {b, c, d, e}. Высота нечеткого множества А - h(A)=0.85. Точка перехода - u=b. Множество А

– субнормально. Нормализованное множество будет иметь вид:

A = (0/a, 0.6/b, 0.7/c, 0.8/d, 1/e).

2. Пусть универсальное множество U представляет собой интервал [0, 100], и переменная u, принимающая значения из этого интервала, интерпретируется как «Возраст».

Тогда нечеткое множество A, обозначаемое термином «Старый», можно определить функцией принадлежности вида

0,						при0 ≤ u ≤ 50
		u −50			−2	−1	(1.5)
µA (u) =
	1	+				, при 50 < u ≤ 100
			5

Здесь носитель S(A) = (50, 100]. Высота множества «Старый» близка к 1, соответственно множество нормальное. Точкой перехода является значение u=55.

7

3. Пусть U = [0, 100] и переменная u, принимающая значения из этого интервала, интерпретируется как «Возраст». Тогда нечеткое множество «Молодой», можно определить функцией принадлежности вида

1,			при1 ≤ u ≤ 25
		1		(1.6)
µМолодой (u) =			, при 25 < u ≤ 100
	1	+ ((u − 25)/ 5)2

Нечеткое множество «Молодой» на универсальном множестве

U′={Иванов, Петров, Сидоров, …} задается с помощью функции принадлежности µМолодой(u) на U = [0, 100], называемой по отношению к U′

функцией совместимости, при этом:

µМолодой(Петров) = µМолодой(u),

где u – возраст Петрова.

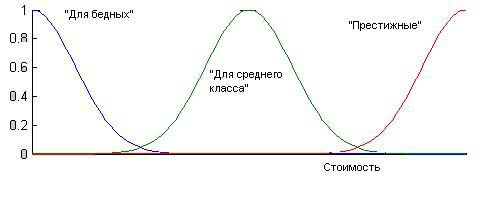
4. Пусть U = {Запорожец, Жигули, Мерседес, …} – множество марок автомобилей, а U′ = [0,∞) – универсальное множество «Стоимость. Тогда на

U′ можно определить нечеткие множества типа: «Для бедных», «Для среднего класса», «Престижные», с функциями принадлежности вида рис. 1.1.

Рис.1.1. Примеры функций принадлежности

Имея эти функции и зная стоимости автомобилей из U в данный момент времени, мы тем самым определим на U′ нечеткие множества с этими же названиями.

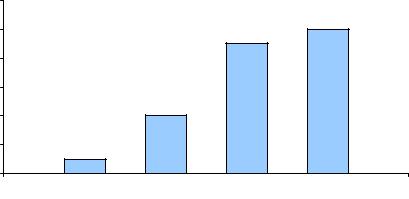
Так, например, нечеткое множество «Престижные», заданное на универсальном множестве U = {Запорожец, Жигули, Мерседес, …} выглядит как показано на рисунке 1.2.

8

1,2
1	Феррари
	Мерседес
0,8
0,6
0,4	Жигули
0,2	Запорожец
0	Стоимость
	Рис.1.2. Пример задания нечеткого множества

Аналогично можно определить нечеткое множество «Скоростные», «Средние», «Тихоходные» и т.д.

5. Пусть U = {-8, -5, -3, 0, 1, 2, 4, 6, 9} – множество целых чисел. Тогда нечеткое подмножество чисел, по абсолютной величине близких к нулю, можно определить, например, так:

А = {0/-8, 0.5/-5, 0.7/-3, 1/0, 0.9/1, 0.8/2, 0.6/4, 0.4/6, 0/9}

	Нечеткое	подмножество универсального множества U может быть
сть	подмножеством	другого нечеткого или обычного	подмножества (то есть с
	функцией принадлежности, принимающей значения 0 или 1) множества А.
	Опр.1.6. А есть подмножество В или содержится в В тогда и только
	тогда, когда µА(u) ≤ µВ(u) для любого u U, то есть
	A B µА(u) ≤ µВ(u) , u U.		(1.7)
	Пример
	Если универсальное множество U = {a, b, c, d}, определенные на нем
	нечеткие подмножества А и В равны соответственно A = (0.5/a, 0.8/b, 0.3/d),
	B = (0.7/a, 1/b, 0.3/c, 1/d), то A B.
	Опр.1.7. Множеством α-уровня нечеткого множества А является
	обычное множество Аα всех таких элементов универсального множества U,
	степень принадлежности которых нечеткому множеству А больше или равна α:
		Аα = {u | u U , µА(u) ≥ α}.	(1.8)

9

Множество α-уровня называют иногда сечением α нечеткого множества

А. Причем, если µА(u) ≥ α, то говорят о сильном сечении, если µА(u) > α, то о

слабом сечении.

Нечеткое множество А можно разложить по его множествам уровня следующим образом:

	A = ∑αAα	( 1 . 9 )
	α
	где αАα - произведение числа α на множество Аα . Знак Σ - знак
	объединения множеств Аα по α.

Пример

Если нечеткое множество А = {0.3/a, 0.4/d, 0.7/c, 0.8/f, 0.6/b}, то множеством α-уровня при α=0.7 будет множество А0.7 = {c, f}. Множество А,

разложенное по его множествам α-уровня, имеет вид:

А= 0.3 {a, d, c, f , b} 0.4{d, c, f, b} 0.6{c, f, b} 0.7{c, f} 0.8{f}

1.2.Методы построения функции принадлежности

Рассмотрим более подробно физический смысл функции принадлежности. Спектр мнений по этому вопросу чрезвычайно широк. Так, например, очень часто на функцию принадлежности накладывается условие нормировки, тем самым, выбирая в качестве функции принадлежности плотность распределения вероятности. В работе Лотфи А. Заде «Fuzzy sets» предполагается, что функция принадлежности - это некоторое “невероятностное субъективное измерение неточности”, и что она отлична от плотности вероятности и от функции распределения вероятности. Иногда под функцией принадлежности понимают возможность или полезность того или иного события.

Наиболее распространенным является суждение, предложенное в работе Л.А. Заде «Понятие лингвистической переменной и его применение к принятию приближенных решений». Согласно данному суждению под значением функции принадлежности µА(u) нечеткого множества А для любого u U

10