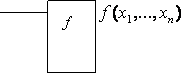Алматинский институт энергетики и связи
Кафедра высшей математики
ДИСКРЕТНАЯ МАТЕМАТИКА
Конспект лекций
для студентов всех форм обучения специальностей
050704 – Вычислительная техника и программное обеспечение,
050703 – Информационные системы
СОСТАВИТЕЛЬ: Л.Н. Астраханцева. Дискретная математика.
Конспект лекций для студентов всех форм обучения специальностей 050704 – Вычислительная техник и программное обеспечение,
050703 – Информационные системы.
Лекции включают три раздела, традиционно изучаемые в курсе дискретной математики: элементы теории множеств и отношений, элементы математической логики и теории графов. Содержание разделов взаимно связано друг с другом. В доступной форме изложены основные теоретические сведения, приведены примеры и решённые задачи, помогающие усвоить и закрепить изучаемый материал. Конспект лекций предназначен для студентов всех форм обучения специальностей 050704 – вычислительная техника и программное обеспечение и 050703 – информационные системы.
1 Элементы теории множеств
1.1 Лекция 1. Множества
Содержание лекции: понятие множества, способы задания, операции над множествами; диаграммы Эйлера-Венна.
Цели лекции: ввести новые понятия, изучить операции над множествами.
Множество – совокупность некоторых объектов (элементов).
Обозначения: A, B, X,… - множества; a, b, x, x1, x2,… - элементы множеств;
![]() -
элемент а принадлежит А.
-
элемент а принадлежит А.
![]() -
элемент b
не принадлежит А. Конечные множества
состоят из конечного числа элементов,
бесконечные – из бесконечного числа
элементов. Обозначения специальных
множеств:
-
элемент b
не принадлежит А. Конечные множества
состоят из конечного числа элементов,
бесконечные – из бесконечного числа
элементов. Обозначения специальных
множеств:
N – множество натуральных чисел (ω);
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел;
C – множество комплексных чисел;
Ø – пустое множество (не содержит ни одного элемента).
Способы задания множеств:
а) перечислением элементов, например, X={x1, x2,…, xn},
A = {2,4,5,6,8,…};
б) с помощью характеристического свойства: A={x| p(x)} где P(x) – свойство Р, которым обладает элемент x, например, A = {x| sinx=1} или
A={x|
x=![]() };
};
в)
порождающей процедурой, которая описывает
способ получения элементов из уже
имеющихся элементов, например, множество
M={1,2,4,8,16,…}
можно задать так: 1) 1![]() M;
2)m
M;
2)m![]() M
→ 2m
M
→ 2m![]() M.
M.
Определения:
а)
множество В называется подмножеством
множества А, если любой элемент множества
В является элементом множества А:
![]() ;
;
б)
множества А и В называют равными,
если
они состоят из одних и тех же элементов:
![]() и
и
![]() ;
;
в)
если
![]() и
и
![]() ,
то В является собственным подмножеством
множества А:
,
то В является собственным подмножеством
множества А:
![]() -
строгое включение.
-
строгое включение.
Не
путать знаки
![]() и
и
![]() :
:
 -
верно,
-
верно,
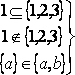 -
не верно.
-
не верно.
Определение.
Совокупность
всех подмножеств множества А называется
его булеаном или множеством-степенью.
Обозначается
Р(А)
или 2А:
Р(А)
= {B|B![]() A}.
Булеан множества из n
элементов содержит 2n
элементов.
A}.
Булеан множества из n
элементов содержит 2n
элементов.
Пример 1.1.1 - A={1,2,3}, Р(А) ={Ø,{1},{2},{3},{1,2},{1,3},{2,3}, A}.
Р(А) содержит 8 элементов, 8=23 .
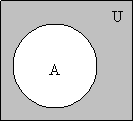
Обычно в конкретных рассуждениях элементы всех множеств берутся из одного достаточно широкого множества U, которое называется универсальным или универсумом.
Операции над множествами
Проиллюстрируем операции над множествами диаграммами
Эйлера - Венна, на которых множества обозначаются точками кругов внутри прямоугольника, точки которого – множество U- универсум.
1
Объединение (сумма) (обозначается
![]() ,
+): А
,
+): А![]() В
= {x|
x
В
= {x|
x![]() А
или x
А
или x![]() В};
В};
 рисунок
1.1.1.
рисунок
1.1.1.
Рисунок 1.1.1
2
Пересечение (произведение,
![]() ,
,
![]() ):
А
):
А![]() В
= {x|
x
В
= {x|
x![]() А
и x
А
и x![]() В};
рисунок 1.1.2.
В};
рисунок 1.1.2.
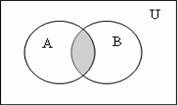
Рисунок 1.1.2
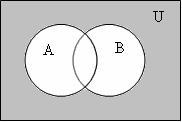
3
Разность ( А \ В; А – В): А \ В = {x|
x![]() А
и x
А
и x![]() В};
рисунок 1.1.3.
В};
рисунок 1.1.3.
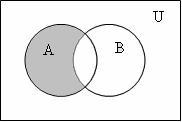
Рисунок 1.1.3
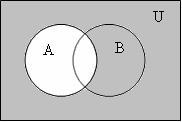
4
Симметрическая разность (![]() ,
,
![]() ,
+): А
,
+): А![]() В=(А
\ В)
В=(А
\ В)![]() (В
\ А) =
(В
\ А) =
{x
| (x![]() А
и x
А
и x![]() В)
или (x
В)
или (x![]() В
и x
В
и x![]() А)};
рисунок 1.1.4.
А)};
рисунок 1.1.4.
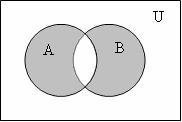
Рисунок 1.1.4
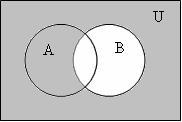
5
Дополнение множества
А
(![]() ):
):![]() ={x
| x
={x
| x![]() и x
и x![]() А}=
U
\ A;
рисунок 1.1.5.
А}=
U
\ A;
рисунок 1.1.5.
|
|
|
|
|
|
Рисунок 1.1.5
Обобщение операций объединения и пересечения
A1![]() A2
A2![]() …
…
![]() An
=
An
=
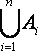
A1![]() A2
A2![]() …
…
![]() An
=
An
=

Алгебра множеств
Большинство
свойств операций над множествами
двойственны: если переставить местами
Ø и U
или
![]() и
и
![]() ,
то из одного свойства можно получить
двойственное.
,
то из одного свойства можно получить
двойственное.
Пусть
задан универсум U,
тогда
![]() A,
B,
C
A,
B,
C
![]() U
выполняются свойства:
U
выполняются свойства:
Т а б л и ц а 1.1.1
|
1 Идемпотентность А |
|
2 Коммутативность А |
|
3 Дистрибутивность А |
|
4 Ассоциативность А |
|
5 Свойство поглощения А |
|
6 Свойство нуля А |
|
7 Свойство единицы А |
|
8 Закон де Моргана
|
|
9
Закон двойного отрицания (инволютивности)
|
|
10 Свойство дополнения A |
Доказать
эти свойства можно либо с помощью
диаграмм Эйлера-Венна, либо формальными
рассуждениями, опирающимися на определение
операций, например, докажем
![]() =
=![]()
![]()
![]() :
:
1 а)
![]() А
А![]() В
В
![]()

в)
![]()
![]()
![]()
![]()
![]()
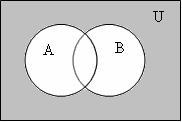
Рисунок 1.1.6
На последних рисунках в пунктах а) и в) отмечена одна и та же область, что доказывает тождество.
2
В формальных рассуждениях исходят из
того, что А=В
![]() А
А
![]() В
и
В
и
В
![]() А,
а последнее имеет место по определению
отношения включения: А
А,
а последнее имеет место по определению
отношения включения: А![]() В:
x
В:
x![]() A
A
![]() x
x![]() B
и В
B
и В![]() А:
x
А:
x![]() B
B
![]() x
x![]() A.
A.
Докажем
![]() =
=![]()
![]()
![]() формальными рассуждениями:ем
формальными рассуждениями:ем
а)
x![]()
![]()
![]() x
x![]() А
А![]() В
В
![]() x
x![]() A
и x
A
и x![]() B
B
![]() x
x![]()
![]() и x
и x![]()
![]()
![]() x
x![]()
![]()
![]()
![]() ;
;
б)
x![]()
![]()
![]()
![]()
![]() x
x![]()
![]() и x
и x![]()
![]()
![]() x
x![]() A
и x
A
и x![]() B
B
![]() x
x![]() А
А![]() В
В![]() ;
;
Теорема. Для любых множеств А и В следующие условия эквивалентны:
а)
А![]() В;
В;
б)
А![]() В=А;
В=А;
в)
А![]() В
=В;
В
=В;
г) А \ В = Ø;
д)
![]()
![]() В
=U.
В
=U.
Установленные выше свойства позволяют упрощать сложные выражения, доказывать новые теоремы и т.д.
Пример
1.1.2
-
![]() .
.
1.2 Лекция 2. Прямое произведение множеств. Отношения
Содержание лекции: разбиения и покрытия множеств; прямое произведение множеств; унарные, бинарные, n-арные отношения; способы задания, основные свойства бинарных отношений.
Цели лекции: ввести ещё одну операцию над множествами – прямое произведение; ввести понятие «отношения».
Разбиения и покрытия множеств
Дано множество А. А ={A1, A2, A3, … An}- множество подмножеств А (семейство подмножеств).
Определение. А называется покрытием множества A, если
1.
![]() Ai
Ai
![]() А
(Ai
А
(Ai![]() A,
Ai≠Ø);
2. A=
A,
Ai≠Ø);
2. A=![]() .
.
Определение. А называется разбиением множества А, если
1.
![]() Ai
Ai
![]() А
(Ai
А
(Ai![]() A,
Ai≠Ø);
2. A=
A,
Ai≠Ø);
2. A=![]() ;
3.
;
3.
![]() Ai,
Aj
Ai,
Aj![]() А
[Ai
≠ Aj
А
[Ai
≠ Aj
![]() А
i
А
i![]() Аj
= Ø].
Аj
= Ø].
Пример 1.2.1 - А={1,2,3}. А1= {{1,2},{2,3},{1,3}} – покрытие;
А2= {{1},{2},{3}} – разбиение; А3= {{1},{2,3}} – разбиение;
А4= {{1},{3}} – множество подмножеств множества А (ни булеан, ни покрытие, ни разбиение).
Пример 1.2.2 - N– множество натуральных чисел.
N0 , N1 - множества чётных и нечётных чисел. N ={ N0, N1}- разбиение N.
Упорядоченные множества. Прямое произведение множеств
Упорядоченные множества из элементов x1,x2,…,xn будем обозначать
(x1,x2,…,xn) или <x1,x2,…,xn> и называть кортеж длины n, упорядоченный набор из n элементов, вектор длины n, n-ка (энка). xi – i-ая координата, компонента.
n=2 - (x1,x2) – пара, упорядоченная двойка;
n=3 - (x1,x2,x3) – тройка, упорядоченная тройка;
n=0 - < > - кортеж, не содержащий элементов.
Если
![]() =(x1,…xn),
=(x1,…xn),
![]() =(y1,…yn),
то
=(y1,…yn),
то
![]()
![]() .
Ясно, что (1,2) ≠ (2,1), {1,2}={2,1}.
.
Ясно, что (1,2) ≠ (2,1), {1,2}={2,1}.
Определение.
Прямым (декартовым) произведением
множеств А и В (обозначается А×В)
называется множество таких пар (a,b),
что a![]() A
и b
A
и b![]() В:
В:
А×В
= {(a,b)| a![]() A
и
b
A
и
b![]() В}.
В}.
![]() Обобщение
прямого
произведения:
A1×A2×…×An={(x1,x2,…,xn)|
a1
Обобщение
прямого
произведения:
A1×A2×…×An={(x1,x2,…,xn)|
a1![]() A1,
a2
A1,
a2![]() A2
,…, an
A2
,…, an![]() An}.
Если
A=B, то
A×A=A2
;
A×A×…×A=An
; A1=A;
A0={Ø}.
An}.
Если
A=B, то
A×A=A2
;
A×A×…×A=An
; A1=A;
A0={Ø}.
n
Пример 1.2.3 - A={1,2}, B={1,2,3}.
A×B ={(1;1),(1;2),(1;3),(2;1),(2;2),(2;3)};
B×A = {(1;1),(1;2),(2;1),(2;2),(3;1),(3;2)}; A×B ≠ B×A;
A2 = {(1,1),(1,2),(2,1),(2,2)};
Пример
1.2.4
- R×R=R2={(a,b)|a,b![]() R,
(a,b) – точки
плоскости}.
R,
(a,b) – точки
плоскости}.
Отношения
Определение.
n-местным
отношением P
(n-местным
предикатом) на множествах А1,А2,…,Аn,
называется любое подмножество прямого
произведения этих множеств: P![]() A1×A2×…×An
и P={(x1,x2,…xn)|
A1×A2×…×An
и P={(x1,x2,…xn)|![]()
![]() A1,…,xn
A1,…,xn![]() An}.
То, что элементы x1,x2,…xn
связаны соотношением Р, записывается
(x1,…,xn)
An}.
То, что элементы x1,x2,…xn
связаны соотношением Р, записывается
(x1,…,xn)
![]() P
или P(x1,…,xn).
Если P
P
или P(x1,…,xn).
Если P![]() An,
то Р – n-местное
отношение на множестве А. n=1,
то P
An,
то Р – n-местное
отношение на множестве А. n=1,
то P![]()
![]() -
одноместное отношение или свойство;
n=3,
то P
-
одноместное отношение или свойство;
n=3,
то P![]() A1×A2×A3
– тернарное отношение.
A1×A2×A3
– тернарное отношение.
Наиболее
часто встречаются и хорошо изучены
бинарные отношения (n=2)
или соответствия P![]() A1×A2,
или P={(x,y)|x
A1×A2,
или P={(x,y)|x![]() A1,
y
A1,
y![]() A2}.
Записывают P(x;y)
или xPy
. Например, вместо <(x;y)
или (x;y)
A2}.
Записывают P(x;y)
или xPy
. Например, вместо <(x;y)
или (x;y)![]() <
записывают x<y.
Далее будем рассматривать бинарные
отношения, называя их просто отношениями.
<
записывают x<y.
Далее будем рассматривать бинарные
отношения, называя их просто отношениями.
Определение.
Областью
определения отношения Р (обозначается
DP)
называется DP
={x
| для некоторого y,
(x,y)![]() P};
областью значений (обозначается EP)
называется EP
={y
| для некоторого x,
(x,y)
P};
областью значений (обозначается EP)
называется EP
={y
| для некоторого x,
(x,y)![]() P}
(т.е. DP-
это множество первых координат пар Р,
EP
–
вторых).
P}
(т.е. DP-
это множество первых координат пар Р,
EP
–
вторых).
Отношение можно задать перечислением элементов, характеристическим свойством, графически, с помощью матриц.
Бинарные отношения на конечных множествах обычно задаются либо списком пар, либо матрицей.
Определение.
Пусть
A={a1,a2,…,am},
B={b1,b2,…,bn}
и P
![]() A×B.
Матрица [P]
=(pij),
размера m×n,
называется матрицей отношения Р , если
A×B.
Матрица [P]
=(pij),
размера m×n,
называется матрицей отношения Р , если
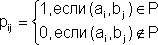 ,
i=1,2,…m;
j-1,2,…n.
,
i=1,2,…m;
j-1,2,…n.
Пример 1.2.5 - A1={1;2}, A2={3;4}. A1×A2={(1,3), (1,4),(2,3),(2,4)}.
P1={(1;3)},
P2={(1;3);(1;4);(2;3)},
тогда
![]() ,
,
![]() .
.
Пример 1.2.6 - A={2,3,4,5,6,7,8};
P={(x,y)
| x,y![]() A,
y
делится на x,
x
≤3} = {(2,4),(2,6),(2,8),(2,2),(3,3),(3,6)}.
A,
y
делится на x,
x
≤3} = {(2,4),(2,6),(2,8),(2,2),(3,3),(3,6)}.
Графическое задание Р:
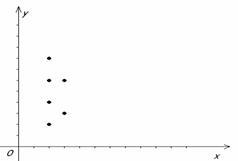
Рисунок 1.2.1
Матричное
задание Р:
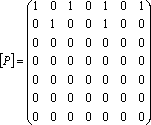 .
.
Определения.
Пусть
P
![]() A×B,
P={(a,b)|a
A×B,
P={(a,b)|a![]() A,
b
A,
b![]() B}.
B}.
а)
P-1
– обратное
Р
![]() P-1
= {(b,a)|(a,b)
P-1
= {(b,a)|(a,b)![]() P},
P-1
P},
P-1![]() B×A;
B×A;
б)
![]() -
дополнение
P
-
дополнение
P![]()
![]() ={(a,b)|(a,b)
={(a,b)|(a,b)![]() P},
P},
![]()
![]() A×B;
A×B;
в) I – тождественное отношение на множестве А (иногда обозначается
idA).
I={(a,a)|a![]() A},
I
A},
I![]() A2
(называют также диагональю в A2
, т.к. его матрицей является единичная
матрица);
A2
(называют также диагональю в A2
, т.к. его матрицей является единичная
матрица);
г)
U
– универсальное отношение
![]() U
={(a,b)|a
U
={(a,b)|a![]() A
и b
A
и b![]() A},
т.е. U=A2.
A},
т.е. U=A2.
Определение. Композицией (произведением) бинарных отношений
P1
![]() A×B
и P2
A×B
и P2
![]() B×C
(обозначается P1
B×C
(обозначается P1![]() P2)
называется отношение
P2)
называется отношение
Р=P1![]() P2
= {(a,c)|a
P2
= {(a,c)|a![]() A,
c
A,
c![]() C
и
C
и
![]() b
b![]() B,
что
(a,b)
B,
что
(a,b)![]() P1
и
(b,c)
P1
и
(b,c)
![]() P2}.
P2}.
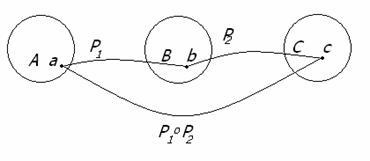
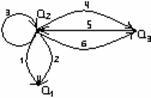
Рисунок 1.2.2
Пример 1.2.7 - A={1,2,3}, B={x,y}; C={ ■, ▲, ●, *}.
Пусть P1={(1,x),(1,y),(3,x)}, P2={(x,■),(x,▲),(y,●),(y,*)}, тогда
P1![]() P2={(1,■),(1,▲),(1,●),(1,*),(3,■),(3,▲)}.
P2={(1,■),(1,▲),(1,●),(1,*),(3,■),(3,▲)}.
Пример
1.2.8
- P1={(x,x+2)|x![]() Z+},
P2={(x,x2)|x
Z+},
P2={(x,x2)|x![]() Z+},
тогда
Z+},
тогда
P1![]() P2={(x,(x+2)2)|
x
P2={(x,(x+2)2)|
x![]() Z+},
P2
Z+},
P2![]() P1={(x,x2+2)|
x
P1={(x,x2+2)|
x![]() Z+}.
Z+}.
Теорема. Для любых бинарных отношений P, Q, R выполняются следующие свойства:
а) (P-1)-1=P;
б)
(P![]() Q)-1=Q-1
Q)-1=Q-1![]() P-1;
P-1;
в)
(P![]() Q)
Q)
![]() R=P
R=P![]() (Q
(Q![]() R).
R).
Основные свойства матриц бинарных отношений
1
Пусть
P,Q
![]() A×B,
[P]=(pi,j),
[Q]=(qi,j).
A×B,
[P]=(pi,j),
[Q]=(qi,j).
[P![]() Q]=(pij+qij)=[P]+[Q],
где элементы матриц складываются по
правилам:
Q]=(pij+qij)=[P]+[Q],
где элементы матриц складываются по
правилам:
0+0=0,
1+0=0+1=1+1=1; [P![]() Q]=(pij*qij)=[P]*[Q],
где умножение элементов матриц происходит
по правилам: 0*0=0*1=0*1=0, 1*1=1.
Q]=(pij*qij)=[P]*[Q],
где умножение элементов матриц происходит
по правилам: 0*0=0*1=0*1=0, 1*1=1.
2
Если
P![]() A×B,
Q
A×B,
Q![]() B×C,
то [P
B×C,
то [P![]() Q]=
Q]=![]() - обычное умножение матриц, но элементы
матриц [P]
и [Q]
складываются и умножаются по правилам
из свойства 1).
- обычное умножение матриц, но элементы
матриц [P]
и [Q]
складываются и умножаются по правилам
из свойства 1).
3 Если P-1 – обратное P, то [P-1]=[P]T.
4
P![]() Q
и [P]=(pij),
[Q]=(qij),
тогда pij≤qij.
Q
и [P]=(pij),
[Q]=(qij),
тогда pij≤qij.
5
I–тождественное
отношение, то
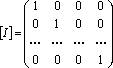 -
единичная матрица.
-
единичная матрица.
6
![]() -
дополнение Р, то [
-
дополнение Р, то [![]() ]
равна матрице отношения Р, в которой
нули заменены единицами и единицы
нулями.
]
равна матрице отношения Р, в которой
нули заменены единицами и единицы
нулями.
Пример 1.2.9 -
![]() ,
,
![]() ,
тогда
,
тогда
![]() ;
;
![]() ;
;
![]() .
.
Свойства отношений
Пусть
P![]() A2.
Отношение Р называется:
A2.
Отношение Р называется:
а)
рефлексивным
![]()
![]() a
a![]() A,
(a,a)
A,
(a,a)![]() P;
P;
б)
антирефлексивным
![]()
![]() a
a![]() A,
(a,a)
A,
(a,a)![]() P
или
[(a,b)
P
или
[(a,b)![]() P
P
![]() a≠b];
a≠b];
в)
симметричным
![]() (a,b)
(a,b)![]() P,
P,![]() (b,a)
(b,a)![]() P;
P;
г)
антисимметричным
![]() (a,b)
(a,b)![]() P
и (b,a)
P
и (b,a)![]() P
P![]() a=b;
a=b;
д)
транзитивным![]() (a,b)
(a,b)![]() P
и (b,с)
P
и (b,с)![]() P
P![]() (a,c)
(a,c)![]() P.
P.
Заметим, что если
а)
P-рефлексивное
![]() I
I![]() P,
[P]=
P,
[P]=
 ;
;
б)
P
– симметричное
![]() P=P-1,
[P]=[P]T;
P=P-1,
[P]=[P]T;
в)
Р-антисимметричное
![]() Р
Р![]() Р-1
Р-1
![]() I,
[P
I,
[P![]() P-1]=[P]*[P-1],
все элементы последней матрицы вне
главной диагонали равны 0;
P-1]=[P]*[P-1],
все элементы последней матрицы вне
главной диагонали равны 0;
г)
P-
транзитивное
![]() P
P![]() P
P![]() P,
т.е. если [P
P,
т.е. если [P![]() P]=(aij),
[P]=(pij),
то aij≤pij.
P]=(aij),
[P]=(pij),
то aij≤pij.
Пример
1.2.10
- А = {1,2,3}, P
= {(1,2),(2,3),(3,2)}, [P]= :
:
а)
P
не рефлексивное, т.к. на главной диагонали
нет единиц; б) P
не симметричное, т.к.(1;2)![]() P→(2;1)
P→(2;1)![]() P
или [P]≠[P]T;
в) P
не антисимметричное, т.к. (2;3)
P
или [P]≠[P]T;
в) P
не антисимметричное, т.к. (2;3)![]() P,
(3;2)
P,
(3;2)![]() P→2≠3
или в матрице
P→2≠3
или в матрице
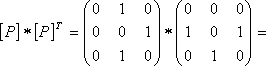
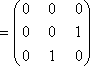 не
все элементы вне главной диагонали
нули; г) P
не
не
все элементы вне главной диагонали
нули; г) P
не
транзитивное,
т.к., например, (1,2)![]() P,
(2,3)
P,
(2,3)![]() P,
но (1,3)
P,
но (1,3)![]() P.
P.
1.3 Лекция 3. Специальные виды бинарных отношений
Содержание лекции: отношения эквивалентности, порядка, функциональные отношения.
Цели лекции: знакомство с бинарными отношениями, обладающими определённым набором свойств.
Отношение эквивалентности
Определение. P называют отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно (обозначается ~, E, ≡).
Примеры отношений эквивалентности: а) отношение равенства на любом множестве: 1)x=x; 2) x=y→y=x; 3) x=y; y=z → x=z; б) отношение подобия на множестве треугольников.
Определение.
Пусть
Е – отношение эквивалентности на
множестве А и х![]() А.
Подмножество элементов множества А,
эквивалентных x,
называется классом эквивалентности
элемента х. Обозначается: [x]E;
E(x).
Таким образом, E(x)={y
| yEx}.
А.
Подмножество элементов множества А,
эквивалентных x,
называется классом эквивалентности
элемента х. Обозначается: [x]E;
E(x).
Таким образом, E(x)={y
| yEx}.
Определение.
Множество классов эквивалентности
называется фактор – множеством множества
А относительно эквивалентности Е,
обозначается А/Е: А/Е={E(x)|
x![]() A}.
Фактор – множество является подмножеством
булеана.
A}.
Фактор – множество является подмножеством
булеана.
Пример 1.3.1 - А – множество студентов в институте. Е – отношение принадлежности к одной группе. [x]E- студенты одной группы. А/Е – множество студенческих групп института.
Из
определений ясно, что 1) любой элемент
класса эквивалентности порождает класс
эквивалентности, т.е. b![]() [a]→[a]=[b];
2) каждый класс эквивалентности содержит
хотя бы один элемент, т.е.
[a]→[a]=[b];
2) каждый класс эквивалентности содержит
хотя бы один элемент, т.е.
![]() а
а![]() А
[a]≠Ø;
3) никакой элемент множества А не может
принадлежать двум различным классам:
aEb
А
[a]≠Ø;
3) никакой элемент множества А не может
принадлежать двум различным классам:
aEb![]() [a]=[b].
[a]=[b].
Теорема.
Фактор
– множество А/Е является разбиением
множества А. Обратно, если
А={Ai}
какое-то разбиение множества А, то ему
соответствует некоторое отношение
эквивалентности Е: xEy![]() x,y
x,y![]() Ai
для некоторого i.
Ai
для некоторого i.
Таким образом, существует взаимно однозначное соответствие между множеством всех разбиений множества А и множеством всех отношений эквивалентности на множестве А.
Пример 1.3.2 - А={1,2,3,4}. А={{1},{2,3,4}}={A1,A2}- разбиение А.
E={(x;y)|x,y![]() Ai,i=1,2}={(1,1),(2,2),(2,3),(2,4),(3,2),(3,3),(3,4),(4,2),(4,3),(4,4)}-
отношение эквивалентности, соответствующее
данному разбиению.
Ai,i=1,2}={(1,1),(2,2),(2,3),(2,4),(3,2),(3,3),(3,4),(4,2),(4,3),(4,4)}-
отношение эквивалентности, соответствующее
данному разбиению.
Пример
1.3.3
- A={1,2,3,4,5,6}, P![]() A2,
P={(1;1);(2;2);(3;3);(4;4);(5;5);(6;6);
(1;2);(1;4);(2;1);(2;4);(3;5);(5;3);(4;1);(4;2)}. Покажем,
что данное отношение является отношением
эквивалентности. По его матрице [P]=
A2,
P={(1;1);(2;2);(3;3);(4;4);(5;5);(6;6);
(1;2);(1;4);(2;1);(2;4);(3;5);(5;3);(4;1);(4;2)}. Покажем,
что данное отношение является отношением
эквивалентности. По его матрице [P]=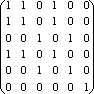 определяем, что P-рефлексивно,
симметрично, транзитивно (см. выше),
следовательно, Р есть отношение
эквивалентности на множестве А. Построим
классы эквивалентности и фактор –
множество: [1]P={x
| (x;1)
определяем, что P-рефлексивно,
симметрично, транзитивно (см. выше),
следовательно, Р есть отношение
эквивалентности на множестве А. Построим
классы эквивалентности и фактор –
множество: [1]P={x
| (x;1)![]() P}={1,2,4};
[2]P={x
| (x;2)
P}={1,2,4};
[2]P={x
| (x;2)![]() P}={1,2,4};
[3]P={x
| (x;3)
P}={1,2,4};
[3]P={x
| (x;3)![]() P}={3,5};
[4]P={x
| (x;4)
P}={3,5};
[4]P={x
| (x;4)![]() P}={1,2,4};
[5]P={x
| (x;5)
P}={1,2,4};
[5]P={x
| (x;5)![]() P}={3,5};
[6]P={x
| (x;6)
P}={3,5};
[6]P={x
| (x;6)![]() P}={6}.
P}={6}.
Таким
образом, имеется только три различных
класса эквивалентности [1]=[2]=[4]={1,2,4},
[3]=[5]={3,5}, [6]={6}. Фактор – множество A/Р=
![]() =
{{1,2,4},{3,5},{6}} является разбиением множества
А, которое соответствует данному
отношению эквивалентности.
=
{{1,2,4},{3,5},{6}} является разбиением множества
А, которое соответствует данному
отношению эквивалентности.
Отношение порядка
Определение.
Отношение
Р на множестве А называется отношением
порядка, если оно антисимметрично и
транзитивно. Часто обозначатся символом
![]() .
.
Если
к тому же оно 1) рефлексивно, то называется
частичным или нестрогим порядком (≤);
2) антирефлексивно, то называется
отношением строгого порядка (<). Если
на множестве А задан порядок
![]() ,
то часто записывают (А,
,
то часто записывают (А,
![]() )
и называют множество А упорядоченным.
)
и называют множество А упорядоченным.
Определение.
Пусть
на множестве А задано отношение порядка
![]() ,
если для любых двух элементов a
и b
этого множества имеет место a
,
если для любых двух элементов a
и b
этого множества имеет место a![]() b
или b
b
или b![]() a,
то элементы называются сравнимыми, в
противном случае несравнимыми.
a,
то элементы называются сравнимыми, в
противном случае несравнимыми.
Определение. Частичный порядок на множестве А называется линейным или цепью, если любые два элемента этого множества сравнимы. Множество, на котором определен частичный (линейный) порядок, называется частично упорядоченным множеством (ч.у.м) ( линейно упорядоченным множеством (л.у.м)).
Пример 1.3.4 - A={a,b,c}. P={(a,a),(a,b),(b,b),(c,c)} – отношение
частичного порядка (т.е. рефлексивно, антисимметрично, транзитивно), что
легко
проверить по его матрице [P]= .
Р не является линейным порядком, т.к.
элементы a
и c,
b
и c
не сравнимы.
.
Р не является линейным порядком, т.к.
элементы a
и c,
b
и c
не сравнимы.
Примерами л.у. множеств являются N, Z, Q, R, где определён естественный порядок.
Определение. Элемент a упорядоченного множества А называется минимальным (максимальным), если в А нет таких элементов x, что x<a (x>a). Л.у.м. называется вполне упорядоченным множеством (в.у.м), если любое его непустое подмножество имеет минимальный элемент.
Пример
1.3.5
- (N;
≤) – в.у.м.;
([0;1]; ≤) – не является в.у.м., т.к., например,
(0;1]
![]() [0;1],
но (0;1] не содержит наименьшего элемента.
[0;1],
но (0;1] не содержит наименьшего элемента.
Определение. Рассмотрим ч.у.м. (Х,≤). Говорят, что элемент у
покрывает
элемент х, если х≤у и не существует
такого элемента z
(z![]() x,z
x,z![]() y),
что х
y),
что х![]() z
z![]() y.
y.
В случае конечного множества Х, ч.у.м. (Х,≤) можно представить в виде схемы, в которой каждый элемент изображается точкой на плоскости. Если у покрывает х, то точки х и у соединяют отрезком, причём точку, соответствующую х, располагают ниже точки у. Такие схемы называют диаграммами Хассе.
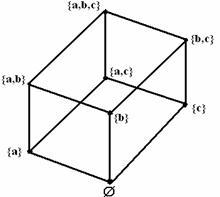
Пример
1.3.6
-
![]() .
Рассмотрим ч.у.м. (Р(А),
.
Рассмотрим ч.у.м. (Р(А),
![]() )
=
)
=
![]() ,
где Р(А)
булеан А. Диаграмма Хассе для (
Р(А),
,
где Р(А)
булеан А. Диаграмма Хассе для (
Р(А),
![]() )
на рисунке 1.3.1
)
на рисунке 1.3.1
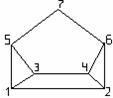
![]()
Рисунок 1.3.1 Рисунок 1.3.2
Пример
1.3.7
- Для л.у.м.
![]() с
обычным отношением порядка на множестве
натуральных чисел, не превосходящих
четырёх, диаграмма Хассе изображена на
рисунке 1.3.2.
с
обычным отношением порядка на множестве
натуральных чисел, не превосходящих
четырёх, диаграмма Хассе изображена на
рисунке 1.3.2.
Функциональные отношения (функции)
Определение.
Бинарное
отношение f![]() А×В
– называется функциональным или функцией
из множества А в множество В, если:
А×В
– называется функциональным или функцией
из множества А в множество В, если:
а)
(x,y1)![]() f,
(x,y2)
f,
(x,y2)![]() f
→ y1=y2
или
f
→ y1=y2
или
![]() x
x![]() A
A![]() !
y
!
y![]() B,
(x,y)
B,
(x,y)
![]() f;
f;
б)
Df=A,
Ef![]() B;
(если Df
B;
(если Df![]() A,
то f
называют частичной функцией), где Df
-
область определения функции, Ef
-
область значений.
A,
то f
называют частичной функцией), где Df
-
область определения функции, Ef
-
область значений.
Пример 1.3.8 - F ={(1,2);(2,3),(3,2)} – функция, т.к. Df = Ef = {1,2,3}.
Пример 1.3.9 - P={(1,1),(1,2),(2,3)} – не функция, т.к. содержит пары (1,1) и (1,2) с одинаковыми первыми и разными вторыми элементами.
Пример
1.3.10
- Отношение
![]() -
функция, т.к. из того, что
-
функция, т.к. из того, что
![]() следует
следует
![]() .
.
Пример
1.3.11
- P={(x2,x)|x![]() R}
– не функция, т.к. содержит пары с
одинаковыми первыми и разными вторыми
элементами: (1,-1)
R}
– не функция, т.к. содержит пары с
одинаковыми первыми и разными вторыми
элементами: (1,-1)
![]() P,
(1;1)
P,
(1;1)
![]() P.
P.
Если
задана функция f
= {(x,y)
| x![]() A,
y
A,
y![]() B},
то x-
аргумент, y-функция.
Различные обозначения функции: y=f(x),
f:
A→B,
f:
x→y;
A
B},
то x-
аргумент, y-функция.
Различные обозначения функции: y=f(x),
f:
A→B,
f:
x→y;
A![]() B
, x
B
, x![]() у.
Говорят также, что f
ставит в соответствие элементу х элемент
у.
у.
Говорят также, что f
ставит в соответствие элементу х элемент
у.
Пусть
f
= {(x,y)|
x![]() A,
y
A,
y![]() B}
– функция. Она называется:
B}
– функция. Она называется:
а)
инъективной (инъекцией, разнозначной),
если (x1,y)
![]() f
и (x2,y)
f
и (x2,y)
![]() f
→ x1=x2
(или
x1≠x2
→ f(x1)
≠ f(x2)),
при этом
f
→ x1=x2
(или
x1≠x2
→ f(x1)
≠ f(x2)),
при этом
![]() -
частичная функция;
-
частичная функция;
б) сюръективной (сюръекцией, отображением А на В),
если
![]() y
y![]() B
B![]() x
x![]() A,
что (x;y)
A,
что (x;y)![]() f,
т.е. Ef
=
B;
f,
т.е. Ef
=
B;
в)
биективной (биекцией, взаимнооднозначным
соответствием), если является и инъективной
и сюръективной. Обозначается А![]() В.
В.

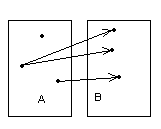
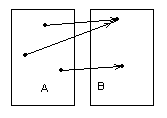
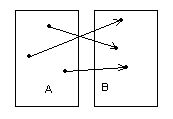
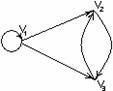
Отношение, но не функция Инъекция, но не сюръекция
Рисунок 1.3.3 Рисунок 1.3.4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сюръекция, но не инъекция Биекция
Рисунок 1.3.5 Рисунок 1.3.6
Если
биекция f:
А![]() А,
то она называется подстановкой множества
А. Простейший пример подстановки есть
тождественное отношение I.
А,
то она называется подстановкой множества
А. Простейший пример подстановки есть
тождественное отношение I.
Пример
1.3.12
- Рассмотрим три функции
![]() :
:
![]() .
.
1
![]() -
инъекция, но не сюръекция, т.к. Df
=
R,
Ef
-
инъекция, но не сюръекция, т.к. Df
=
R,
Ef
![]() R
(рисунок 1.3.7).
R
(рисунок 1.3.7).
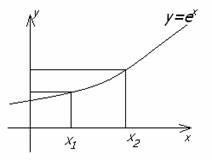
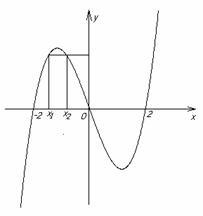
Рисунок 1.3.7 Рисунок 1.3.8
2
![]() -
сюръективна, но не инъективна, Ef
=
R
(рисунок 1.3.8).
-
сюръективна, но не инъективна, Ef
=
R
(рисунок 1.3.8).
3
![]() -
биективна.
-
биективна.
Заметим, что свойства этих, а также других функций, проще всего определять по их графикам.
2 Элементы математической логики
2.1 Лекция 4. Алгебра логики
Содержание лекции: логика высказываний; логические операции;
формулы и функции алгебры логики.
Цели лекции: знакомство с основными понятиями и операциями
алгебры логики.
Логика высказываний
Определение. Высказыванием называется повествовательное предложение, о котором в данной ситуации можно говорить, что оно истинно или ложно.
Пример 2.1.1 - Высказывание «дважды два – четыре» - истинно; высказывание «тенге – российская валюта» - ложно.
Определение. Простое (элементарное) высказывание рассматривается как некое неделимое целое. Обозначается А, В, С,...,Р,…; сложным (составным) называется высказывание, составленное из простых с помощью логических связок (операций).
Основными логическими операциями (связками) являются:
а) конъюнкция (операция «и», логическое произведение).
Конъюнкцией
двух высказываний P и Q (обозначается
![]() ,
читается “Р и Q”) называется высказывание,
истинное тогда и только тогда, когда
истинны оба высказывания и ложное во
всех остальных случаях;
,
читается “Р и Q”) называется высказывание,
истинное тогда и только тогда, когда
истинны оба высказывания и ложное во
всех остальных случаях;
б)
дизъюнкция (операция «или», логическая
сумма). Дизъюнкцией двух высказываний
P и Q (обозначается
![]() ,
читается “Р или Q”) называется
высказывание, ложное, если оба высказывания
ложные и истинное во всех остальных
случаях;
,
читается “Р или Q”) называется
высказывание, ложное, если оба высказывания
ложные и истинное во всех остальных
случаях;
в)
отрицание (инверсия). Отрицанием
высказывания P (обозначается
![]() ,
читается “не Р”) называется высказывание,
истинное, когда P ложное и ложное, когда
P истинное;
,
читается “не Р”) называется высказывание,
истинное, когда P ложное и ложное, когда
P истинное;
г)
импликация (логическое следование).
Импликацией
двух
высказываний P и Q (обозначается
![]() ,
,
![]() ,
читается “если Р то Q”, «Р влечёт Q”)
называется высказывание, ложное, когда
Р истинное, а Q ложное и истинное во всех
остальных случаях;
,
читается “если Р то Q”, «Р влечёт Q”)
называется высказывание, ложное, когда
Р истинное, а Q ложное и истинное во всех
остальных случаях;
д) эквиваленция (эквивалентность). Эквиваленцией двух высказываний
P
и Q (обозначается
![]()
![]()
![]() ,
читается “Р эквивалентно Q”, “Р тогда
и только тогда, когда Q”) называется
высказывание, истинное, когда P и Q оба
истинны или оба ложны и ложное во всех
остальных случаях.
,
читается “Р эквивалентно Q”, “Р тогда
и только тогда, когда Q”) называется
высказывание, истинное, когда P и Q оба
истинны или оба ложны и ложное во всех
остальных случаях.
Алгебра логики
Рассмотрим содержание логики высказываний, используя язык алгебры логики, которая изучает строение логических высказываний (т.е. логических формул) и способы установления их истинности с помощью алгебраических методов.
Поставим в соответствие высказыванию P логическую переменную х, которая принимает значение 1, если Р истинно; 0, если Р ложно. Из логических переменных можно с помощью логических операций составлять различные конструкции, которые являются формулами алгебры логики.
Если
формула
![]() построена
из логических переменных, принадлежащих
множеству
построена
из логических переменных, принадлежащих
множеству
![]() ,
то будем писать
,
то будем писать
![]() .
.
Действия логических операций задаются таблицами истинности. Составим таблицы истинности в соответствии с определением логических операций:
Т а б л и ц а 2.1.1
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
Исходя из таблиц истинности для логических операций, можно строить таблицы истинности для произвольных формул.
Пример 2.1.2 - Построить таблицу истинности для формулы
![]() .
.
Т а б л и ц а 2.1.2
|
|
у |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
Т а б л и ц а 2.1.3
|
|
у |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Введём новые важные логические операции, добавляя к пяти основным ещё три:
е)
штрих Шеффера
(антиконъюнкция).
Обозначается
![]() .
.
По
определению
![]() или
или
![]() ;
;
ж)
стрелка Пирса
(антидизъюнкция).
Обозначается
![]() .
.
По
определению
![]() или
или
![]() ;
;
и) кольцевая сумма (логическое сложение, сложение по модулю два).
Обозначается
![]() .
По определению
.
По определению
![]() или
или
![]() .
.
Составим таблицы истинности этих операций, исходя из определений.
Т а б л и ц а 2.1.4
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
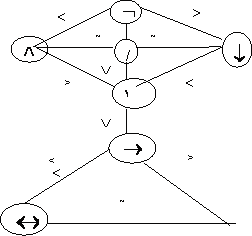
При тождественных преобразованиях, при составлении формул важно знать приоритеты операций (какая сильнее, какая слабее), как раскрывать скобки. Для этих целей приняты следующие соглашения:
а)
внешние скобки не пишутся, например,
вместо
![]() будем
писать
будем
писать
![]() ;
;
б)
на множестве
![]() вводится
транзитивное отношение
вводится
транзитивное отношение
«>» - быть более сильным и отношение «~» - быть равносильным, по правилам, указанным на схеме.
|
|
|
|
|
|
Рисунок 2.1.1
Согласно этим соглашениям недостающие скобки в формуле расставляют последовательно, начиная с наиболее сильных связок и кончая наиболее слабыми, а для равносильных связок расстановка скобок выполняется слева направо.
Пример
2.1.4
-
а) в формуле
![]() скобки
следует расставить так:
скобки
следует расставить так:
![]() ;
б) в формуле
;
б) в формуле
![]() скобки
расставляются так:
скобки
расставляются так:
![]() ;
в) в формуле
;
в) в формуле
![]() скобки
опустить нельзя, т.к. в силу наших
соглашений выражению
скобки
опустить нельзя, т.к. в силу наших
соглашений выражению
![]() соответствует
формула
соответствует
формула
![]() .
.
Функции алгебры логики
Каждая формула представляет логическую функцию от логических переменных, которые могут принимать только два значения 0 и 1.
Определение.
Функцией
алгебры логики
(логической
функцией)
от
n
переменных
![]() (обозначается
(обозначается![]() )
называется любая функция, которая
произвольному набору
)
называется любая функция, которая
произвольному набору
![]() нулей
и единиц ставит в соответствие значение
нулей
и единиц ставит в соответствие значение
![]() ,
т.е.
,
т.е.
![]() .
.
Функции
алгебры логики называются также булевыми,
двоичными или переключательными
(обозначаются
в некоторых учебниках
![]() ).
).
Дело
в том, что эти функции описывают
преобразование некоторым устройством
входных сигналов в выходные. Пусть
устройство имеет n входов
![]() ,
на
которые
может
подаваться или не подаваться ток, и один
выход, на который ток подаётся или не
подаётся, в зависимости от подачи тока
на входы (см. рисунок 2.1.2).
,
на
которые
может
подаваться или не подаваться ток, и один
выход, на который ток подаётся или не
подаётся, в зависимости от подачи тока
на входы (см. рисунок 2.1.2).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
![]()
![]()
![]()
![]()
![]()
![]()
Рисунок 2.1.2 Рисунок 2.1.3
Значение
![]() понимается
как поступление тока на i-ый
вход;
понимается
как поступление тока на i-ый
вход;
![]() -
как не поступление. Значение
-
как не поступление. Значение
![]() (где
(где
![]() ),
если ток на выходе проходит и
),
если ток на выходе проходит и
![]() -
если не проходит.
-
если не проходит.
Так,
например, функции
![]() ,
представляющей операцию конъюнкции,
соответствует устройство с двумя входами
и одним выходом (см. рисунок 2.1.3). При
этом значение выхода равно 1 тогда и
только тогда, когда оба значения входов
равно 1.
,
представляющей операцию конъюнкции,
соответствует устройство с двумя входами
и одним выходом (см. рисунок 2.1.3). При
этом значение выхода равно 1 тогда и
только тогда, когда оба значения входов
равно 1.
2.2 Лекция 5. Логические функции
Содержание лекции: способы задания логических функций; основные эквивалентные соотношения алгебры логики.
Цели лекции: знакомство с различными способами задания функций и понятием эквивалентности формул.
Способы задания функций:
а)
задание таблицей истинности, в левой
части которой выписаны все возможные
наборы значений аргументов
![]() ,
а
в правой – столбец значений
,
а
в правой – столбец значений
![]() ,
соответствующих этим наборам. Число
всех наборов 0 и 1 функции n
переменных будет равно
,
соответствующих этим наборам. Число
всех наборов 0 и 1 функции n
переменных будет равно
![]() ,
т.е. для функции одной переменной -
,
т.е. для функции одной переменной -
![]() ,
двух -
,
двух -
![]() ,
трёх -
,
трёх -
![]() и
т.д. Таким образом, таблица истинности
функции одной переменной содержит 2
строки, двух – 4, трёх – 8 и т.д. При этом
множество аргументов принято упорядочивать
по лексикографическому порядку, который
лежит в основе упорядочения слов в
различных словарях. Практически этот
порядок можно получить, если первый
столбец таблицы разделить на две части
и первую половину заполнить нулями,
вторую – единицами; затем второй столбец
разделить на четыре части и заполнить
их, чередуя 0 и 1, начинать с нулей; третий
столбец разделить на восемь частей,
которые заполнить, чередуя 0 и 1, начинать
с нулей, и т.д;
и
т.д. Таким образом, таблица истинности
функции одной переменной содержит 2
строки, двух – 4, трёх – 8 и т.д. При этом
множество аргументов принято упорядочивать
по лексикографическому порядку, который
лежит в основе упорядочения слов в
различных словарях. Практически этот
порядок можно получить, если первый
столбец таблицы разделить на две части
и первую половину заполнить нулями,
вторую – единицами; затем второй столбец
разделить на четыре части и заполнить
их, чередуя 0 и 1, начинать с нулей; третий
столбец разделить на восемь частей,
которые заполнить, чередуя 0 и 1, начинать
с нулей, и т.д;
б)
задание функций перечислением всех
наборов, на которых
![]() принимает
значение 0 (нулевые наборы) и всех наборов,
на которых она принимает значение 1
(единичные наборы);
принимает
значение 0 (нулевые наборы) и всех наборов,
на которых она принимает значение 1
(единичные наборы);
в) задание функции формулой;
г)
задание с помощью вектора значений.
Вектором значений функции
![]() называется
упорядоченный набор всех значений
называется
упорядоченный набор всех значений
![]() ,
при котором все значения упорядочены
по лексикографическому порядку множества
аргументов
,
при котором все значения упорядочены
по лексикографическому порядку множества
аргументов
![]() .
.
Рассмотрим на примере эти способы задания функции.
Пример
2.2.1
- Имеется устройство, фиксирующее
принятие некоторой резолюции тремя
персонами (комитетом трёх). Каждый член
комитета при одобрении резолюции
нажимает свою кнопку. Если большинство
членов согласны, то резолюция принята,
что фиксирует устройство. Таким образом,
устройство реализует функцию
![]() ,
таблица истинности которой имеет вид:
Т а б л и ц а 2.2.1
,
таблица истинности которой имеет вид:
Т а б л и ц а 2.2.1
|
x |
y |
z |
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Зададим
эту функцию нулевыми и единичными
наборами:
![]() -
нулевые наборы;
-
нулевые наборы;
![]()
![]() -
единичные наборы. Если задавать эту
функцию с
-
единичные наборы. Если задавать эту
функцию с
помощью вектора значений, то это будет набор (00010111).
Итак,
число всех наборов 0 и 1 для функции n
переменных равно
![]() .
Число же всех возможных различных
функций n переменных равно числу всех
возможных расстановок 0 и 1 в столбце с
.
Число же всех возможных различных
функций n переменных равно числу всех
возможных расстановок 0 и 1 в столбце с
![]() строками,
т.е. равно
строками,
т.е. равно
![]() .
Значит, если
.
Значит, если
![]() -
множество всех значений аргументов
функции
-
множество всех значений аргументов
функции
![]() ,
а
,
а
![]() -
множество всех функций от
-
множество всех функций от
![]() ,
то
мощности этих множеств будут
,
то
мощности этих множеств будут
![]() .
Таким образом,
.
Таким образом,
![]() растёт
очень быстро:
растёт
очень быстро:
![]() ,
,
![]() ,
,
![]() и
т.д.
и
т.д.
Особую
роль в алгебре логики играют функции
одной и двух переменных. Например,
множество всех логических функций одной
переменной
![]() состоит
из четырёх функций, которые можно
представить их таблицей истинности:
состоит
из четырёх функций, которые можно
представить их таблицей истинности:
Т а б л и ц а 2.2.2
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
|
0 |
|
|
1 |
Функции
![]() и
и
![]() константы
0 и 1,
константы
0 и 1,
![]() =х
– повторяет переменную х, (эти операции,
говорят, не существенны или фиктивны).
Наибольший интерес представляет функция
=х
– повторяет переменную х, (эти операции,
говорят, не существенны или фиктивны).
Наибольший интерес представляет функция
![]() =
=![]() -
унарная операция отрицания. Аналогичным
образом можно построить таблицу
истинности для всех 16 (
-
унарная операция отрицания. Аналогичным
образом можно построить таблицу
истинности для всех 16 (![]() )
функций двух переменных. Среди них 7
логических операций (конъюнкция,
дизъюнкция, и т.д.), остальные не
представляют интереса. Заметим, что
функция может быть представлена как
операция, если её значения лежат в
области определения этой функции. В
этом смысле все функции математической
логики могут быть представлены операциями.
)
функций двух переменных. Среди них 7
логических операций (конъюнкция,
дизъюнкция, и т.д.), остальные не
представляют интереса. Заметим, что
функция может быть представлена как
операция, если её значения лежат в
области определения этой функции. В
этом смысле все функции математической
логики могут быть представлены операциями.
Логические функции трёх и более переменных обычно задаются либо таблицей истинности, либо формулой, состоящей из знаков переменных и знаков унарных и бинарных операций. В общем случае формула описывает логическую функцию как суперпозицию других более простых функций.
Определение.
Функцию![]() называют суперпозицией функций
называют суперпозицией функций
![]() и
и
![]() ,
если
,
если
![]() .
.
Пример
2.2.2
- Функция
![]() есть
суперпозиция
есть
суперпозиция
![]() и
и
![]() ,
,
![]() ,
,
![]() .
.
Эквивалентность формул. Основные эквивалентные соотношения алгебры логики
В
одном из примеров выше (см. пример 2.2) в
составленной таблице истинности два
столбца, для
![]() и
для
и
для
![]() ,
были одинаковы. В этом случае возникает
понятие эквивалентности формул.
,
были одинаковы. В этом случае возникает
понятие эквивалентности формул.
Определение.
Формулы
![]() и
и
![]() называются
эквивалентными или равносильными
(обозначается
называются
эквивалентными или равносильными
(обозначается
![]() ,
,
![]() ),
если они представляют одну и ту же
функцию.
),
если они представляют одну и ту же
функцию.
Пример
2.2.3
- а) в примере 2.1.2 функции
![]() и
и
![]() эквивалентны,
т.е.
эквивалентны,
т.е.
![]() =
=![]() ;
;
б)
построим таблицы истинности для формул
![]() :
:
Т а б л и ц а 2.2.3
|
x |
y |
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
![]() .
.
В этом примере для установления эквивалентности формул применён метод построения их таблиц истинности и сравнения полученных таблиц по каждому набору значений переменных.
Другим методом являются эквивалентные преобразования формул, которые используют эквивалентные соотношения (законы) и правила замены.
Корректность преобразований обеспечивается выполнением следующих двух правил:
а) если в исходном эквивалентном соотношении все вхождения
переменной
х одновременно заменены формулой
![]() ,
то получим новое эквивалентное
соотношение;
,
то получим новое эквивалентное
соотношение;
б)
если какая либо формула
![]() ,
описывающая функцию
,
описывающая функцию![]() ,
содержит
,
содержит
подформулу
![]() ,
то замена
,
то замена
![]() на
на
![]() (
(![]() )
не изменит функции
)
не изменит функции![]() .
.
Перечислим основные эквивалентные соотношения или законы.
Т а б л и ц а 2.2.4
|
1 Коммутативность |
|
|
|
|
2 Ассоциативность |
|
|
|
|
3 Дистрибутивность |
|
|
|
|
4 Идемпотентность |
|
|
|
|
5 Закон поглощения |
|
|
|
|
6 Закон де Моргана |
|
|
|
|
7
Закон двойного отрицания
|
|||
|
8 Свойства констант |
|
|
|
|
9
|
|
||
|
|
|
|
|
Наряду с основными эквивалентностями, часто используют ещё некоторые, которые можно вывести из основных или доказать с помощью таблиц истинности; сведём их также в таблицу.
Т а б л и ц а 2.2.5
|
10 Закон склеивания |
|
|
10а Закон расщепления |
|
|
11 Обобщённое склеивание |
|
|
12
|
12а
|
|
13
|
13а
|
|
14
|
|
|
15
|
16
|
|
17
|
18
|
Заметим, что основные эквивалентные законы (таблица 2.2.4) не
выводятся друг из друга, доказать их справедливость можно с помощью таблиц истинности.
Определение.
Формула
![]() называется
выполнимой (опровержимой), если существует
такой набор значений переменных, при
котором формула принимает значение 1
(0).
называется
выполнимой (опровержимой), если существует
такой набор значений переменных, при
котором формула принимает значение 1
(0).
Пример
2.2.4
- Формула
![]() =
=![]() является одновременно и выполнимой и
опровержимой, т.к. (
является одновременно и выполнимой и
опровержимой, т.к. (![]() и
и
![]() .
.
Определение.
Формула
![]() называется
тождественно истинной, общезначимой
или тавтологией (тождественно ложной
или противоречием), если эта формула
принимает значение 1 (соответственно
0) при всех наборах значений переменных
(т.е. функция является константой 1 (0)).
называется
тождественно истинной, общезначимой
или тавтологией (тождественно ложной
или противоречием), если эта формула
принимает значение 1 (соответственно
0) при всех наборах значений переменных
(т.е. функция является константой 1 (0)).
Пример
2.2.5
- Формула
![]() -
тождественно истинна, т.к.
-
тождественно истинна, т.к.
![]() =1
для всех х
; формула
=1
для всех х
; формула
![]() -
тождественно ложна, т.к.
-
тождественно ложна, т.к.
![]() =0
для всех х:
=0
для всех х:
Т а б л и ц а 2.2.6
|
х |
|
|
|
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
Если
![]() -
тождественно истинная формула, то будем
писать
-
тождественно истинная формула, то будем
писать
![]()
![]() .
Если
.
Если
![]() -
тождественно ложная - то
-
тождественно ложная - то
![]()
![]() .
Заметим, что, так как формула может
представлять какое-то логическое
высказывание или рассуждение, то это
рассуждение будет логически правильным,
если представляющая его формула
тождественно истинна.
.
Заметим, что, так как формула может
представлять какое-то логическое
высказывание или рассуждение, то это
рассуждение будет логически правильным,
если представляющая его формула
тождественно истинна.![]()
2.3 Лекция 6. Дизъюнктивные и конъюнктивные нормальные формы
Содержание лекции: полные системы логических функций; ДНФ и КНФ; СДНФ и СКНФ.
Цели
лекции: выяснение причин предпочтения
базиса
![]() ;
приведение к ДНФ и КНФ; приведение к
СДНФ и СКНФ.
;
приведение к ДНФ и КНФ; приведение к
СДНФ и СКНФ.
Булева алгебра логических функций. Полные системы логических функций
Одна
и та же логическая функция может быть
задана формулами, включающими различные
наборы логических операций. Например,
![]() .
Существуют наборы логических операций
(функций), через которые можно выразить
любые другие логические функции.
.
Существуют наборы логических операций
(функций), через которые можно выразить
любые другие логические функции.
Определение.
Система
логических
функций
![]() называется
функционально полной системой или
базисом, если любая логическая функция
является суперпозицией функций из
называется
функционально полной системой или
базисом, если любая логическая функция
является суперпозицией функций из
![]() .
.
Примерами функционально полных систем являются:
![]() и
другие.
и
другие.
Наиболее
хорошо изученным является базис
![]() .
Формулы, содержащие, кроме переменных
и скобок, только операции конъюнкции,
дизъюнкции и отрицания, называются
булевыми.
.
Формулы, содержащие, кроме переменных
и скобок, только операции конъюнкции,
дизъюнкции и отрицания, называются
булевыми.
Теорема. Всякая логическая функция может быть представлена булевой формулой (т.е. как суперпозиция конъюнкции, дизъюнкции и отрицания).
Отсюда
следует, что система
![]() =
=![]() функционально полна. Для доказательства
функциональной полноты какого - либо
другого набора
функционально полна. Для доказательства
функциональной полноты какого - либо
другого набора
операций достаточно показать, что через операции набора можно выразить конъюнкцию, дизъюнкцию и отрицании. Справедливо и более общее утверждение.
Теорема.
Если
все функции функционально полной системы
![]() представимы
формулами над
представимы
формулами над
![]() ,
то
,
то
![]() также
функционально полна.
также
функционально полна.
![]() Пример
2.3.1
-
Рассмотрим
системы
Пример
2.3.1
-
Рассмотрим
системы
![]() =
=![]() и
и
![]() =
=![]() и базис
и базис
![]() =
=![]() .
Докажем, что
.
Докажем, что
![]() ,
,
![]() также
базисы. Действительно, в каждой их этих
систем недостающая до
также
базисы. Действительно, в каждой их этих
систем недостающая до
![]() операция
может быть выражена через остальные
две: для
операция
может быть выражена через остальные
две: для
![]() не
достаёт «
не
достаёт «![]() »:
»:![]()
для
![]() не
достаёт «
не
достаёт «![]() »:
»:![]()
![]() .
.
Формула
![]() в
системах
в
системах
![]() ,
,
![]() перейдёт
соответственно в формулы:
перейдёт
соответственно в формулы:
![]()
![]() ,
,
![]()
![]() .
.
Таким
образом, с точки зрения функциональной
полноты систему
![]() можно
считать избыточной, т.к. она сохраняет
свойство полноты и при удалении из неё
дизъюнкции или конъюнкции. Но, как мы
видим, за
можно
считать избыточной, т.к. она сохраняет
свойство полноты и при удалении из неё
дизъюнкции или конъюнкции. Но, как мы
видим, за
неизбыточность
систем
![]() ,
,
![]() приходится
платить избыточностью формул, т.к. каждая
замена одной операции на другую по
формулам (
приходится
платить избыточностью формул, т.к. каждая
замена одной операции на другую по
формулам (![]() )
вносит в формулу лишнее отрицание.
Поскольку, как было сказано выше, базис
)
вносит в формулу лишнее отрицание.
Поскольку, как было сказано выше, базис
![]() =
=![]() наиболее изучен и имеет самое широкое
применение на практике, то другие базисы
приводятся к нему. Рассмотрим различные
методы приведения к этому базису.
наиболее изучен и имеет самое широкое
применение на практике, то другие базисы
приводятся к нему. Рассмотрим различные
методы приведения к этому базису.
Дизъюнктивные и конъюнктивные нормальные формы
Определение. Элементарной конъюнкцией (дизъюнкцией) называется конъюнкция (дизъюнкция) переменных или их отрицаний.
Пример
2.3.2
- а)
![]() и
и
![]() элементарные
дизъюнкции; б)
элементарные
дизъюнкции; б)
![]() и
и
![]() элементарные
конъюнкции; в)
элементарные
конъюнкции; в)![]() одновременно
является и элементарной дизъюнкцией и
элементарной конъюнкцией.
одновременно
является и элементарной дизъюнкцией и
элементарной конъюнкцией.
Определение. Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций.
Пример
2.3.3
- а)![]() ДНФ,
б)
ДНФ,
б)
![]() КНФ.
КНФ.
Теорема. Любая формула может быть приведена к ДНФ (КНФ) (т.е. любая формула эквивалентна некоторой ДНФ (КНФ)).
Правило приведения формулы к ДНФ:
а)
все логические операции, присутствующие
в формуле, выразить через
![]() ,
используя эквивалентности:
,
используя эквивалентности:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
б) перенести все отрицания к переменным по закону де Моргана:
![]() ;
;
в)
используя закон дистрибутивности,
преобразовать формулы так, чтобы все
конъюнкции выполнялись раньше дизъюнкций:
![]() .
.
Пример
2.3.4
- Привести к ДНФ формулу
![]() .
.
Решение:
заменим
![]() на
на
![]() ,
затем применим закон де Моргана и закон
двойного отрицания:
,
затем применим закон де Моргана и закон
двойного отрицания:
![]() =
=![]() =
=
![]()
![]() .
.
Заметим, что последняя формула в примере в некоторых учебниках уже считается ДНФ, в других же считают, что в элементарных конъюнкциях и дизъюнкциях каждая переменная должна встречаться не более одного раза. Для удаления лишних переменных применяют следующие эквивалентности:
а)
![]() (закон
идемпотентности); б)
(закон
идемпотентности); б)
![]() (закон
исключённого третьего),
(закон
исключённого третьего),
![]() (закон
противоречия); в)
(закон
противоречия); в)
![]() ,
,
![]() -
( свойства констант).
-
( свойства констант).
Используя
закон идемпотентности, в последнем
примере получим ДНФ:
![]() .
.
Правило приведения формулы к КНФ.
Приведение
формулы к КНФ производится также, как
к ДНФ, только вместо пункта в) применятся
пункт
![]() ):
):
![]() )
используя закон дистрибутивности,
преобразовать формулы так, чтобы все
дизъюнкции выполнялись раньше конъюнкций:
)
используя закон дистрибутивности,
преобразовать формулы так, чтобы все
дизъюнкции выполнялись раньше конъюнкций:
![]() .
.
Пример
2.3.5
- Привести к КНФ формулу
![]() .
.
Решение:
заменим операцию
![]() ,
используя формулу
,
используя формулу
![]() :
:
![]() [закон
де Моргана, двойное
[закон
де Моргана, двойное
отрицание]
=![]() - КНФ.
- КНФ.
СДНФ и СКНФ
ДНФ и КНФ имеют тот недостаток, что они не обладают свойством единственности, т.е. одна и та же формула имеет несколько ДНФ и КНФ. Этим недостатком не обладают совершенные нормальные формы.
Определение. Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой в каждую элементарную конъюнкцию каждая переменная входит ровно один раз, причём, входит либо сама переменная, либо её отрицание, и среди элементарных конъюнкций не должно быть одинаковых.
Определение. Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ, в которой в каждую элементарную дизъюнкцию каждая переменная входит ровно один раз, причём, входит либо сама переменная, либо её отрицание, и среди элементарных дизъюнкций не должно быть одинаковых.
Пример
2.3.6
- а)
![]() -
СДНФ; б)
-
СДНФ; б)
![]()
![]() -
СКНФ; в)
-
СКНФ; в)
![]() -
не СДНФ, т.к. содержит две одинаковых
элементарных конъюнкции; г)
-
не СДНФ, т.к. содержит две одинаковых
элементарных конъюнкции; г)
![]() -
не СДНФ, т.к. в одной элементарной
конъюнкции содержится и переменная, и
её отрицание:
-
не СДНФ, т.к. в одной элементарной
конъюнкции содержится и переменная, и
её отрицание:
![]() .
.
Теорема. (Существование и единственность СДНФ и СКНФ). Всякая логическая формула единственным образом (с точностью до порядка следования элементарных конъюнкций (дизъюнкций)) может быть представлена в СДНФ (СКНФ).
Для приведения формулы к СДНФ можно использовать один из двух методов.
І
метод: а) приводим формулу к ДНФ; б) если
какая-то элементарная конъюнкция не
содержит некоторой переменной у, то
добавляем её, используя закон расщепления:
![]() ;
в) убираем одинаковые элементарные
конъюнкции, используя закон идемпотентности
;
в) убираем одинаковые элементарные
конъюнкции, используя закон идемпотентности
![]() .
.
Пример
2.3.7
- Получить СДНФ функции
![]() ,
заданной в ДНФ.
,
заданной в ДНФ.
Решение:
![]()
![]()
![]()
![]() -
СДНФ.
-
СДНФ.
ІІ
метод:
для
данной формулы строим таблицу истинности,
потом применяем правило, основанное на
теореме Шеннона: СДНФ функции
![]() содержит
столько элементарных конъюнкций, сколько
единиц в столбце значений
содержит
столько элементарных конъюнкций, сколько
единиц в столбце значений
![]() ;
каждому единичному набору нулей и единиц
;
каждому единичному набору нулей и единиц
![]() соответствует
элементарная конъюнкция всех переменных,
в которой
соответствует
элементарная конъюнкция всех переменных,
в которой
![]() взято
с отрицанием, если
взято
с отрицанием, если
![]() и
без отрицания, если
и
без отрицания, если
![]() .
.
Пример
2.3.8
- Дана ДНФ функции
![]() .
Найти СДНФ.
.
Найти СДНФ.
Решение: построим таблицу истинности (таблица 2.3.1).
Т а б л и ц а 2.3.1
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
Функция
принимает значение 1 при следующих
значениях аргументов:
![]() -
это её единичные наборы. По выше
приведённому правилу
-
это её единичные наборы. По выше
приведённому правилу
![]() -
СДНФ.
-
СДНФ.
Приведение
формулы к СКНФ аналогично приведению
к СДНФ. Также существует два метода: а)
метод элементарных преобразований; б)
СКНФ находят по таблице истинности:
СКНФ функции
![]() содержит
столько элементарных дизъюнкций, сколько
нулей в столбце значений
содержит
столько элементарных дизъюнкций, сколько
нулей в столбце значений
![]() ;
каждому нулевому набору нулей и единиц
;
каждому нулевому набору нулей и единиц
![]() соответствует
элементарная дизъюнкция всех переменных,
в которой
соответствует
элементарная дизъюнкция всех переменных,
в которой
![]() взято
с отрицанием, если
взято
с отрицанием, если
![]() и
без отрицания, если
и
без отрицания, если
![]() .
.
Пример
2.3.9
- Рассмотрим функцию из предыдущего
примера
![]() .
Приведём её к СКНФ двумя способами:
.
Приведём её к СКНФ двумя способами:
а)
![]()
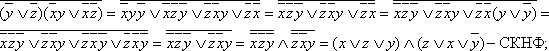
б)
из таблицы истинности 2.3.1 выпишем нулевые
наборы:![]() ,
значит, по выше приведённому правилу
,
значит, по выше приведённому правилу
![]()
![]() -
СКНФ.
-
СКНФ.
2.4 Лекция 7. Минимизация булевых функций
Содержание лекции: минимизация булевых функций в классе ДНФ; карты Карно; понятие двойственности.
Цели лекции: выяснить смысл понятия минимизации; рассмотреть один из практических методов минимизации.
Минимизация булевых функций в классе ДНФ
При решении практических задач часто возникает проблема минимизации логических формул, например, найти формулу, содержащую наименьшее число переменных или наименьшее число операций, или наименьшее количество подформул определённого вида и т.д. К настоящему времени наиболее изучена задача отыскания дизъюнктивных форм, минимальных по числу вхождений переменных.
Под вхождением переменной понимается место, которое переменная занимает в формуле.
Определение. Минимальной ДНФ (МДНФ) называется ДНФ с наименьшим числом вхождений переменных.
Карты Карно
Существует много способов отыскания МДНФ (метод Квайна, неопределённых коэффициентов, с помощью гиперкубов и т.д.). Остановимся на наиболее простом – с использованием карт (диаграмм) Карно.
Карта
Карно
–
это таблица, каждая клетка (ячейка)
которой соответствует некоторой
элементарной конъюнкции всех переменных.
Для функции n переменных
![]() существует
существует
![]() возможных
комбинаций их значений, состоящих из 0
и 1. То есть, например, для n=2 имеем
возможных
комбинаций их значений, состоящих из 0
и 1. То есть, например, для n=2 имеем
![]() элементарные
конъюнкции
элементарные
конъюнкции
![]() ,
которым соответствуют следующие наборы
0 и 1: (1,1), (1,0), (0,1), (0,0); для n=3 -
,
которым соответствуют следующие наборы
0 и 1: (1,1), (1,0), (0,1), (0,0); для n=3 -
![]() -
-
![]() -
(1,1,1), (1,1,0),…,(0,0,0) и т.д.
-
(1,1,1), (1,1,0),…,(0,0,0) и т.д.
Карты
Карно строятся в виде таблицы размером
![]() ,
так, что её
,
так, что её
столбцы
соответствуют значениям переменных
![]() ,
строки
-
,
строки
-
![]() (или
наоборот); вообще, для одной и той же
функции может быть построено несколько
карт, важно, чтобы соседние ячейки (как
по вертикали, так и по горизонтали)
отличались только значением одной
переменной. Мы будем рассматривать, в
основном, функции двух, трёх и четырёх
переменных. Для них карты Карно имеют
следующий вид: а)для функции двух
переменных х,
у
карта Карно на рисунке 2.4.1; б) для функции
трёх переменных
(или
наоборот); вообще, для одной и той же
функции может быть построено несколько
карт, важно, чтобы соседние ячейки (как
по вертикали, так и по горизонтали)
отличались только значением одной
переменной. Мы будем рассматривать, в
основном, функции двух, трёх и четырёх
переменных. Для них карты Карно имеют
следующий вид: а)для функции двух
переменных х,
у
карта Карно на рисунке 2.4.1; б) для функции
трёх переменных
![]() -
на
-
на
рисунке
2.4.2; в) для функции четырёх переменных
![]() -
на рисунке 2.4.3.
-
на рисунке 2.4.3.
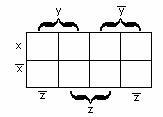
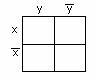
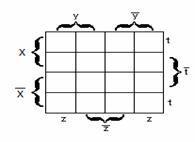
Рисунок 2.4.1 Рисунок 2.4.2 Рисунок 2.4.3
Для определения МДНФ булевой функции, сначала надо найти её СДНФ, затем каждую элементарную конъюнкцию СДНФ отметить единицей в соответствующей ячейке карты Карно.
Пример
2.4.1
- Две функция
![]() и
и
![]() заданы
в форме СДНФ. Для функции
заданы
в форме СДНФ. Для функции
![]() карта
Карно изображена на рисунке 2.4.4, для
карта
Карно изображена на рисунке 2.4.4, для
![]() -
на рисунке 2.4.5.
-
на рисунке 2.4.5.
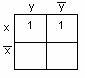
![]()
![]()

Рисунок 2.4.4 Рисунок 2.4.5
Заметим,
что если в картах Карно две, четыре,
восемь (для функции четырёх переменных)
соседних ячеек по вертикали или по
горизонтали содержат 1, то эти ячейки
объединяют в блоки (на картах их отмечают
овалами), и соответствующие этим блокам
дизъюнкции элементарных конъюнкций
можно упростить. Так, в примере 2.4.1 для
функции
![]() имеем
блок из двух ячеек, на рисунке 2.4.4 он
отмечен овалом. Этому блоку соответствует
дизъюнкция
имеем
блок из двух ячеек, на рисунке 2.4.4 он
отмечен овалом. Этому блоку соответствует
дизъюнкция
![]() ,
упрощая которую, получим:
,
упрощая которую, получим:
![]()
![]() .
Таким образом, блоку из двух ячеек
функции двух переменных отвечает одна
переменная х,
а именно та переменная, которая полностью
«покрывает» этот блок. Формула упростилась
.
Таким образом, блоку из двух ячеек
функции двух переменных отвечает одна
переменная х,
а именно та переменная, которая полностью
«покрывает» этот блок. Формула упростилась
![]() .
.
Для
функции
![]() имеем
также один блок из двух ячеек (см. рисунок
2.4.5), ему соответствует дизъюнкция
элементарных конъюнкций
имеем
также один блок из двух ячеек (см. рисунок
2.4.5), ему соответствует дизъюнкция
элементарных конъюнкций
![]() ,
упрощая которую получим
,
упрощая которую получим
![]() ,
т.е. блоку из двух ячеек функции трёх
переменных соответствует конъюнкция
двух переменных, «покрывающих» этот
блок. Формула упростилась
,
т.е. блоку из двух ячеек функции трёх
переменных соответствует конъюнкция
двух переменных, «покрывающих» этот
блок. Формула упростилась
![]() .
.
Рассмотрим ещё несколько примеров.
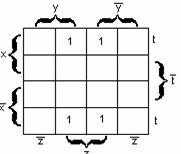 Пример
2.4.2
-
Пример
2.4.2
-
![]() -
СДНФ функции. Её карта Карно на рисунке
2.4.6. Так как z
находится на обоих концах карты, то её
(карту) можно «скрутить» и считать, что
1 в углах карты образуют блок из четырёх
ячеек. Эти четыре ячейки полностью
покрывает переменная z, т.о., МДНФ функции
будет
-
СДНФ функции. Её карта Карно на рисунке
2.4.6. Так как z
находится на обоих концах карты, то её
(карту) можно «скрутить» и считать, что
1 в углах карты образуют блок из четырёх
ячеек. Эти четыре ячейки полностью
покрывает переменная z, т.о., МДНФ функции
будет
![]() .
.
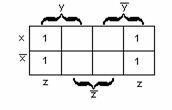
Рисунок 2.4.6 Рисунок 2.4.7
Пример
2.4.3
-
![]() -СДНФ
функции. Её карта Карно на рисунке 2.4.7.
На карте есть блок из четырёх ячеек,
который покрывают переменные
-СДНФ
функции. Её карта Карно на рисунке 2.4.7.
На карте есть блок из четырёх ячеек,
который покрывают переменные
![]() и
и
![]() ,
поэтому МДНФ функции будет:
,
поэтому МДНФ функции будет:
![]() .
.
Пример
2.4.4
-
![]()
![]()
![]() -
СДНФ. Карта Карно этой функции на рисунке
2.4.8.
-
СДНФ. Карта Карно этой функции на рисунке
2.4.8.

Рисунок 2.4.8
Имеем:
1) блок из 8 ячеек покрывает переменная
y;
2) двум блокам из 4 ячеек соответствуют
элементарные конъюнкции
![]() и
и
![]() .
Поэтому МДНФ будет:
.
Поэтому МДНФ будет:
![]() .
.
Двойственность
Определение.
Функция![]() называется двойственной к функции
называется двойственной к функции
![]() ,
если
,
если
![]() ;
функция, двойственная к самой себе,
;
функция, двойственная к самой себе,
называется
самодвойственной, т.е.
![]() .
.
Отношение
двойственности симметрично, т.е., если
![]() ,то
,то
![]() .
Пример
2.4.5
-
.
Пример
2.4.5
-
Т а б л и ц а 2.4.1
|
|
1 |
0 |
|
|
|
|
|
|
0 |
1 |
|
|
|
|
а)
для
![]() =
=![]() имеем
имеем
![]() ;
;
б)
для
![]() ,
т.е. отрицание самодвойственное
,
т.е. отрицание самодвойственное
![]() .
.
Двойственную
функцию можно получить также с помощью
таблиц истинности, заменяя в таблице
истинности функции
![]() все
значения на противоположные.
все
значения на противоположные.
Пример
2.4.6
- Получим для функции
![]() двойственную
функцию двумя способами:
двойственную
функцию двумя способами:
I
способ:
![]()
![]() ;
;
II
способ: построим таблицу истинности
для
![]() (таблица
2.4.2), затем заменим в ней все значения
на противоположные, получим таблицу
для
(таблица
2.4.2), затем заменим в ней все значения
на противоположные, получим таблицу
для
![]() (таблица
2.4.3). По таблицам видно, что эта функция
самодвойственна
(таблица
2.4.3). По таблицам видно, что эта функция
самодвойственна
![]() .
.
Т а б л и ц а 2.4.2 Т а б л и ц а 2.4.3
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
2.5 Лекция 8. Изоморфизм булевых алгебр. Некоторые приложения математической логики
Содержание лекции: булева алгебра и теория множеств; коммутационные схемы.
Цели лекции: отметить важность изоморфизма булевых алгебр; указать примеры практического использования выше изложенного материала.
Булева алгебра и теория множеств
Можно легко заметить аналогию между свойствами операций над множествами и свойствами логических операций. Это не случайно.
Определение. Всякая алгебра, содержащая две бинарные и одну унарную операции, которые удовлетворяют соотношениям 1) - 9) (см. основные эквивалентные соотношения булевой алгебры, или основные свойства операций над множествами) называется булевой.
Таким образом, булевыми алгебрами будут:
а)
![]() -
булева алгебра всех логических функций
с операциями конъюнкции, дизъюнкции,
отрицания;
-
булева алгебра всех логических функций
с операциями конъюнкции, дизъюнкции,
отрицания;
б)
![]() -
булева алгебра логических функций m
переменных – это подалгебра алгебры
-
булева алгебра логических функций m
переменных – это подалгебра алгебры
![]() ,
т.к.
,
т.к.
![]() .
.
в)
(P
![]() -
булева алгебра множеств над
-
булева алгебра множеств над
![]() -
универсумом, с операциями пересечения,
объединения, дополнения;
-
универсумом, с операциями пересечения,
объединения, дополнения;
г)
![]() -
булева алгебра двоичных векторов длины
n с логическими операциями над двоичными
векторами, определёнными следующим
образом :
-
булева алгебра двоичных векторов длины
n с логическими операциями над двоичными
векторами, определёнными следующим
образом :
![]()
![]() имеет
место
имеет
место
1)
![]() ,
где
,
где
![]() если
если
![]() ;
в любом другом случае
;
в любом другом случае
![]() ;
;
2)
![]() ,
где
,
где
![]() если
если
![]() ;
в любом другом случае
;
в любом другом случае
![]() ;
;
3)
![]() ,
где
,
где
![]() если
если
![]() ,
,
![]() если
если
![]() .
.
Если
мощности множеств
P
![]()
![]() и
и![]() равны (
равны (![]() P
P![]() ),
то между ними можно установить взаимно
однозначное соответствие, а соответствующие
булевы алгебры будут изоморфны. Изоморфизм
булевых алгебр широко используется в
компьютерных вычислениях, например,
вместо выполнения операций над множествами
или логическими функциями используют
их изоморфные аналоги – поразрядные
операции над двоичными векторами.
),
то между ними можно установить взаимно
однозначное соответствие, а соответствующие
булевы алгебры будут изоморфны. Изоморфизм
булевых алгебр широко используется в
компьютерных вычислениях, например,
вместо выполнения операций над множествами
или логическими функциями используют
их изоморфные аналоги – поразрядные
операции над двоичными векторами.
Коммутационные схемы
Возможность применения математической логики к техническим вопросам была обнаружена в 30-х годах ХХ века. Была замечена, например, связь между электрическими цепями и логическими функциями. Это открытие дало толчок к развитию ЭВМ. Рассмотрим упрощённо эту связь.
Основным элементом релейно-контактных устройств является электромеханическое реле (переключатель). Реле может размыкать и замыкать цепь. Присвоим р значение 1, когда цепь замкнута (ток проходит), и значение 0, когда цепь разомкнута (ток не проходит).
Рассмотрим
электрическую цепь на рисунке 2.5.1. При
таком расположении контактов p и q
лампочка будет гореть (т.е. схема имеет
значение 1), если оба переключателя p и
q замкнуты (т.е. имеют значения 1). Таким
образом, эта схема соответствует
логической формуле
![]() ,
а такое расположение переключателей
называется логическим элементом «p и
q» или схемой логического умножения,
его обозначают на схеме как на рисунке
2.5.2.
,
а такое расположение переключателей
называется логическим элементом «p и
q» или схемой логического умножения,
его обозначают на схеме как на рисунке
2.5.2.
![]()
Рисунок 2.5.1 Рисунок 2.5.2
Рассмотрим
теперь схему на рисунке 2.5.3. В этой цепи
лампочка будет гореть и значение схемы
равно 1, если хотя бы один из двух контактов
p или q, или оба, будут замкнуты, т.е. или
![]() ,
или
,
или
![]() ,
или оба
,
или оба
![]() .
Таким образом, эта схема соответствует
логической формуле
.
Таким образом, эта схема соответствует
логической формуле
![]() ,
а такое расположение переключателей
называется логическим элементом «p или
q» или схемой логического сложения.
Изображают на схемах как на рисунке
2.5.4.
,
а такое расположение переключателей
называется логическим элементом «p или
q» или схемой логического сложения.
Изображают на схемах как на рисунке
2.5.4.
|
|
|
|
|
|
![]()
Рисунок 2.5.3 Рисунок 2.5.4 Рисунок 2.5.5
Если имеем схему с одним переключателем p, который обладает свойством, что лампочка загорается тогда и только тогда, когда p разомкнут (т.е. схема имеет значение 1, когда р=0, и значение 0, когда р=1), то эта схема
соответствует
![]() .
Такой логический элемент называется
«не р» или инвертором, его часто изображают
на схемах как на рисунке 2.5.5.
.
Такой логический элемент называется
«не р» или инвертором, его часто изображают
на схемах как на рисунке 2.5.5.
Рассмотрим примеры схем, реализующих простейшие логические формулы.
Пример
2.5.1
- Схема на рисунке 2.5.6 реализует формулу
(переключательную функцию, или функцию
проводимости)
![]() ;
схема для формулы
;
схема для формулы
![]() изображена
на рисунке 2.5.7; схема на рисунке 2.5.8 для
формулы
изображена
на рисунке 2.5.7; схема на рисунке 2.5.8 для
формулы
![]() .
.
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
Рисунок 2.5.6 Рисунок 2.5.7 Рисунок 2.5.8
Так как любую логическую формулу можно привести к ДНФ или КНФ, то для неё всегда можно построить контактную схему. Очевидно, что чем проще формула, определяющая функцию проводимости, тем проще схема. Поэтому задача упрощения схемы сводится к задаче упрощения или минимизации соответствующих функций. Эту задачу мы решали выше.
Пример 2.5.2 - Упростить схему
Рисунок 2.5.9
Решение: составим переключательную функцию
![]() .
Упростим эту функцию, используя
эквивалентные преобразования.
.
Упростим эту функцию, используя
эквивалентные преобразования.
![]()
![]() .
Последней формуле соответствует
упрощённая схема на рисунке 2.5.10.
.
Последней формуле соответствует
упрощённая схема на рисунке 2.5.10.
3 Элементы теории графов
3.1 Лекция 9. Основные понятия теории графов
Содержание лекции: основные понятия и определения, способы задания графов; смежность, инцидентность, степени вершин.
Цели лекции: знакомство с основными понятиями теории графов.
Основные понятия и определения
Графы описывают связи между объектами, а связи могут быть «направленными» (например, в генеалогическом дереве) или «ненаправленными» (например, сеть дорог с двусторонним движением). Поэтому в теории графов выделяют два основных типа графов: ориентированные (орграф) и неориентированные (неорграф, н-граф). Иногда рассматривают графы смешанного типа.
Определение. Графом G называется совокупность двух множеств: V – вершин и E – рёбер ( для н-графа) или дуг ( для орграфа). Обозначается G=G(V,E) или G=(V,E).
Пусть
![]() -
множество вершин. Тогда для н-графа
-
множество вершин. Тогда для н-графа
![]() ,
где ребра
,
где ребра
![]() -
двухэлементные подмножества множества
V; для орграфа
-
двухэлементные подмножества множества
V; для орграфа
![]() ,
где дуги
,
где дуги
![]() -
упорядоченные пары, т.е.
-
упорядоченные пары, т.е.
![]() .
.
Если
![]() -
ребро (
-
ребро (![]() - дуга), то вершины
- дуга), то вершины
![]() и
и
![]() называются
концами ребра (
называются
концами ребра (![]() -
началом,
-
началом,
![]() -
концом дуги); вершины
-
концом дуги); вершины
![]() и
и
![]() называются
инцидентными ребру (дуге)
называются
инцидентными ребру (дуге)
![]() ,
а ребро (дуга)
,
а ребро (дуга)
![]() инцидентным
(ой)
вершинам
инцидентным
(ой)
вершинам
![]() и
и
![]() ;
вершины
;
вершины
![]() и
и
![]() называются
смежными,
если
они являются концами одного ребра
(дуги).
называются
смежными,
если
они являются концами одного ребра
(дуги).
Ребро (дуга), концевые вершины которого совпадают, называется петлёй. Рёбра (дуги), инцидентные одной и той же паре вершин, называются параллельными или кратными. Граф, содержащий кратные рёбра (дуги), называется мультиграфом. Граф называется конечным, если множества V и E конечны, пустым – если множество его вершин V (а значит и рёбер) пусто. Некоторые вершины могут не войти в список пар множества E, они называются изолированными. Граф, у которого все вершины изолированные, называется нуль-графом; антиподом нуль-графа является полный граф: его рёбрами являются все возможные пары его вершин (у него нет петель и кратных рёбер).
Заметим,
что многие теоремы и определения в
теории графов могут быть отнесены как
к н-графам, так и к орграфам. Часто, когда
совершенно ясно о каком типе графов
идёт речь, рёбра, как и дуги, обозначают
круглыми скобками, т.е. вместо
![]() записывают
записывают
![]() .
Каждому н-графу канонически соответствует
орграф с тем же множеством вершин, в
котором каждое ребро заменено двумя
дугами, инцидентными тем же вершинам и
имеющими противоположные направления.
.
Каждому н-графу канонически соответствует
орграф с тем же множеством вершин, в
котором каждое ребро заменено двумя
дугами, инцидентными тем же вершинам и
имеющими противоположные направления.
Определение.
Степенью
вершины
![]() (обозначается
ρ(v))
называется количество всех инцидентных
ей рёбер.
(обозначается
ρ(v))
называется количество всех инцидентных
ей рёбер.
Если
m – число рёбер н-графа G, то
![]() =2m.
Предполагается, что петля даёт вклад 2
в степень вершины.
=2m.
Предполагается, что петля даёт вклад 2
в степень вершины.
Для вершин орграфа определяются также две локальные степени.
Определение.
Степенью
выхода вершины
![]() (обозначается
(обозначается
![]() или
или
ρ1(v))
называется число дуг с началом в вершине
![]() ;
степенью входа вершины
;
степенью входа вершины
![]() (обозначается
(обозначается![]() или ρ2(v))
- число дуг с концом в вершине
или ρ2(v))
- число дуг с концом в вершине
![]() ;
ρ(v)=
;
ρ(v)=![]() +
+![]() .
Если m – число дуг орграфа G, то
.
Если m – число дуг орграфа G, то![]() =
=![]() =m,
причём петля даёт вклад 1 в обе степени.
=m,
причём петля даёт вклад 1 в обе степени.
Способы задания графов
1.
Задание графа парой множеств V и E , когда
каждое ребро (дуга)
![]() определено
парой инцидентных ему вершин.
определено
парой инцидентных ему вершин.
Пример 3.1.1 - G=G(V,E) - граф , где V={a,b,c}, а) E={{a,b},{b,c}} - для н-графа; б) E={(a,b),(b,c)} - для орграфа.
2. Задание графа рисунком. Вершины обозначаются точками, рёбра – линиями, соединяющими точки; дуги – стрелками. При этом один и тот же граф может быть задан разными рисунками. Например, граф G=G(V,E) из примера 3.1.1, где V={a,b,c}, E={{a,b},{b,c}} можно изобразить так:
![]()

Рисунок 3.1.1
3. Задание графа матрицей инцидентности. Пусть все вершины и рёбра (дуги) графа G=(V,E) пронумерованы: V={v1,v2,v3,…vn},
E={e1,e2,e3,…em}.
Матрицей инцидентности графа G называется
матрица А=(аij)
размера
![]() ,
n
– число вершин, m
– число рёбер (дуг):
,
n
– число вершин, m
– число рёбер (дуг):
а)
для н-графа: aij=![]()
б)
для орграфа: aij=
Пример
3.1.2
- V={v1,v2,v3,
v4}
– множество вершин, E={e1,e2,e3,
e4,
e5}
– множество рёбер, A=
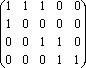 -
матрица инцидентности графа на рисунке
3.1.2; V={а1,а2,а3}
– множество вершин, E={1,2,3,4,5,6} – множество
дуг, A=
-
матрица инцидентности графа на рисунке
3.1.2; V={а1,а2,а3}
– множество вершин, E={1,2,3,4,5,6} – множество
дуг, A= - матрица инцидентности графа на рисунке
3.1.3.
- матрица инцидентности графа на рисунке
3.1.3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 3.1.2 Рисунок 3.1.3
4.
Задание графа матрицей смежности.
Матрицей смежности В=(bij)
графа G=(V,E) называется квадратная матрица
размера n![]() n
(n – число вершин), элементы которой
определены следующим образом:
n
(n – число вершин), элементы которой
определены следующим образом:
а)
для н-графа b
ij=![]()
б)
для орграфа b
ij=![]()
в) для мультиграфа
bij=
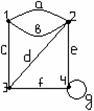 Пример
3.1.3
- Матрица B=
Пример
3.1.3
- Матрица B=
 является
матрицей смежности н-графа, изображённого
на рисунке 3.1.4; матрица B=
является
матрицей смежности н-графа, изображённого
на рисунке 3.1.4; матрица B=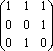 - матрица смежности для орграфа на
рисунке 3.1.5; B=
- матрица смежности для орграфа на
рисунке 3.1.5; B= - матрица смежности для мультиграфа на
рисунке 3.1.6.
- матрица смежности для мультиграфа на
рисунке 3.1.6.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 3.1.4 Рисунок 3.1.5 Рисунок 3.1.6
Заметим, что а) для н-графа матрица смежности симметрическая, т.е. В=Вт, причём, если у графа нет петель, то в матрице смежности по главной диагонали стоят нули; б) для орграфа количество единиц в i-ой строке равно степени выхода ρ1(vі) i-ой вершины; количество единиц в j-ом столбце равно ρ2(vj) – степени входа j-ой вершины.
По
матрице смежности легко определить
число вершин
n
– это размер матрицы; число рёбер - m=![]() .
.
5. Задание графа списком рёбер (дуг). Кроме матрицы инцидентности, отношение инцидентности можно определить списком рёбер (дуг), задавая его в виде двух столбцов, в первом перечислены все рёбра (дуги), во втором - инцидентные им вершины.
Пример 3.1.4 - Для графа на рисунке 3.1.6 список дуг будет иметь вид:
Т а б л и ц а 3.1.1
|
Дуги |
Вершины |
|
a b c d e f g |
1 2 1 2 1 3 2 3 2 4 3 4 4 4 |