АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ

Дискретная математика

Методические указания и задания

к выполнению расчетно-графических работ

(для студентов очной формы обучения специальности

050704 – Вычислительная техника и программное обеспечение)

Часть 2

СОСТАВИТЕЛИ: Л.Н. Астраханцева, Л.Н.Ким, М.Ж.Байсалова. Алгебра и геометрия. Методические указания и задания к выполнению расчетно-графической работы для студентов очной формы обучения специальности 050704 – Вычислительная техника и программное обеспечение.

Методические указания и задания к расчетно-графической работе содержат типовой расчет №3 дисциплины «Алгебра и геометрия» для студентов очной формы обучения специальности 050704 – Вычислительная техника и программное обеспечение. Приведены основные теоретические вопросы программы. Дано решение типового варианта.

1 Типовой расчёт 2. Элементы математической логики

1.1 Теоретические вопросы

1 Основные понятия логики высказываний. Высказывание, основные логические операции.

2 Логические переменные и формулы. Таблицы истинности логических операций и формул. Соглашение о приоритетах логических операций.

3 Функции алгебры логики. Способы задания логических функций (таблица истинности, нулевые и единичные наборы, вектор значений, формула).

4 Эквивалентность формул. Основные эквивалентные соотношения алгебры логики.

5 Полные системы логических функций. Приведение логических формул к ДНФ, КНФ.

6 Совершенные ДНФ и КНФ (СДНФ и СКНФ).

7 Минимизация в классе ДНФ. Карты Карно.

8 Коммутационные схемы.

9 Двойственность. Булева алгебра и теория множеств.

1.2 Расчётные задания

1 Составить таблицы истинности для формул

Т а б л и ц а 1

1.1	1.16
1.2	1.17
1.3	1.18
1.4	1.19
1.5	1.20
1.6	1.21
1.7	1.22
1.8	1.23
1.9	1.24

продолжение таблицы 1

1.10	1.25
1.11	1.26
1.12	1.27
1.13	1.28
1.14	1.29
1.15	1.30

2 Установить эквивалентность формул:

а) с помощью таблиц истинности;

б) приведением формул к СДНФ или СКНФ с помощью эквивалентных преобразований.

Т а б л и ц а 2

2.1 и	2.16 и
2.2 и	2.17 и
2.3 и	2.18 и
2.4 и	2.19 и
2.5 и	2.20 и
2.6 и	2.21 и
2.7 и	2.22 и
2.8 и	2.23 и
2.9 и	2.24 и
2.10и	2.25 и
2.11 и	2.26 и
2.12 и	2.27 и
2.13 и	2.28 и
2.14 и	2.29 и

продолжение таблицы 2

2.15 и

2.30 и

3 Упростить формулы

Т а б л и ц а 3

3.1	3.16
3.2	3.17
3.3	3.18
3.4	3.19
3.5	3.20
3.6	3.21
3.7	3.22
3.8	3.23
3.9	3.24
3.10	3.25
3.11	3.26
3.12	3.27
3.13	3.28
3.14	3.29
3.15	3.30

4 Записать формулы в виде, содержащем только операции , ,  над простыми переменными

Т а б л и ц а 4

4.1	4.16
4.2	4.17
4.3	4.18
4.4	4.19

продолжение таблицы 4

4.5	4.20
4.6	4.21
4.7	4.22
4.8	4.23
4.9	4.24
4.10	4.25
4.11	4.26
4.12	4.27.
4.13	4.28
4.14	4.29
4.15	4.30

5-12 Для данной формулы:

а) составить таблицу истинности;

б) привести к ДНФ;

в) по таблице истинности составить СДНФ;

г) построить карту Карно;

д) с помощью карты Карно найти минимальную ДНФ (МДНФ);

е) от МДНФ перейти к КНФ;

ж) найти СКНФ;

и) по карте Карно найти МКНФ

Т а б л и ц а 5

1	16
2	17
3	18
4	19

продолжение таблицы 5

5	20
6	21
7	22
8	23
9	24
14	29
15	30

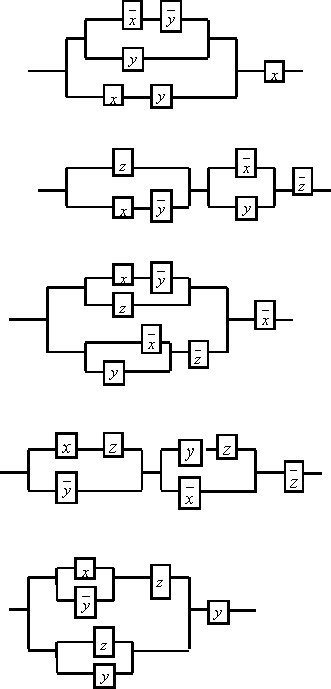
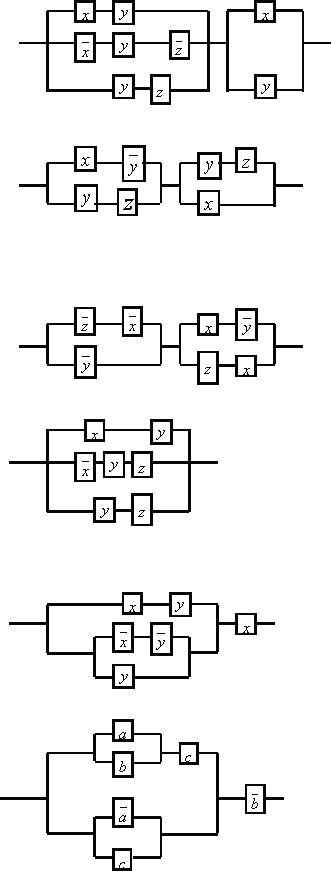
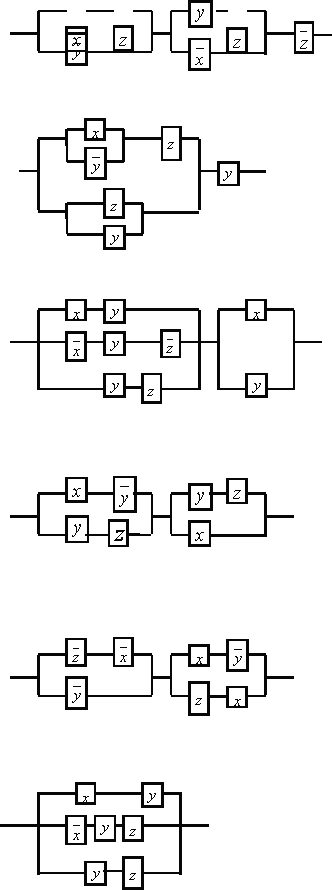
13 Упростить схемы

13.1

13.2

13.3

13.4

13.5

13.6

13.7

13.8

13.9

13.10

13.11

13.14

13.15

13.16

13.16

13.17

13.24

13.30

1.3 Решение типового варианта

1 Установить эквивалентность формул и :

а) с помощью таблиц истинности;

б) приведением формул к СДНФ с помощью элементарных преобразований.

Решение:

а) составим таблицы истинности формул используя таблицы истинности входящих в них операций:

x	y	z
0	0	0	0	0	0	0	0	0	0
0	0	1	1	1	0	0	0	0	0
0	1	0	0	1	0	0	0	0	0
0	1	1	1	1	0	0	0	0	0
1	0	0	1	0	1	0	0	0	0
1	0	1	1	1	1	1	0	1	1
1	1	0	1	1	1	1	1	0	1
1	1	1	1	1	1	1	1	1	1

Так как 7-ой и 10-ый столбцы, т.е. столбцы значений формули совпадают, то эти формулы эквивалентны;

б) преобразуем формулу сначала к дизъюнктивной нормальной форме (ДНФ) используя известные свойства логических операций:

=[дистрибутивность]==

[идемпотентность]=. Последнее выражение является ДНФ формулы . Чтобы получить совершенную дизъюнктивную нормальную форму (СДНФ), добавим недостающие переменные в первую и вторую конъюнкты используя закон расщепления

(): ===[коммутативность, идемпотентность]= = - СДНФ формулы .

Формула задана в ДНФ, поэтому для определения её СДНФ добавим в каждую конъюнкту недостающие переменные:

===[коммутативность,

идемпотентность]= - СДНФ формулы .

Так как СДНФ обеих формул совпадают, то они эквивалентны.

2 Упростить формулу

Решение:

при упрощении формулы будем использовать свойства логических операций: =[используем известную эквивалентность]== дистрибутивность]= ==

[коммутативность, закон противоречия, идемпотентность] =

=[свойство нуля, коммутативность]== [дистрибутивность]=

=[свойство единицы, идемпотентность]=

.

3 Дана формула :

а) привести формулу к ДНФ;

б) построить таблицу истинности;

в) по таблице истинности составить СДНФ;

г) построить карту Карно;

д) с помощью карты Карно найти минимальную ДНФ (МДНФ);

е) от МДНФ перейти к КНФ;

ж) построить СКНФ;

з) по карте Карно найти МКНФ.

Решение:

а) ДНФ формулы получим используя определение операции и свойства логических операций: ==[закон Де-Моргана] = = [двойное отрицание] = ==[дистрибутивность]=

==[идемпотентность]=

=. Последнее выражение является ДНФ данной формулы;

б) построим таблицу истинности формулы:

A	B	C	D
0	0	0	0	1	0	0	0	1	0	1	0
0	0	0	1	1	0	0	0	1	1	0	0
0	0	1	0	1	0	0	0	1	0	1	0
0	0	1	1	1	0	1	1	0	1	0	1
0	1	0	0	1	1	0	1	0	1	0	1
0	1	0	1	1	1	0	1	0	1	0	1
0	1	1	0	1	1	0	1	0	1	0	1
0	1	1	1	1	1	1	1	0	1	0	1
1	0	0	0	0	0	0	0	1	0	1	0
1	0	0	1	0	0	0	0	1	1	0	0
1	0	1	0	0	0	0	0	1	0	1	0
1	0	1	1	0	0	1	1	0	1	0	1
1	1	0	0	0	0	0	0	1	1	0	0
1	1	0	1	0	0	0	0	1	1	0	0
1	1	1	0	0	0	0	0	1	1	0	0
1	1	1	1	0	0	1	1	0	1	0	1

в) составим совершенную дизъюнктивную нормальную форму (СДНФ) формулы по таблице истинности. Для этого выпишем наборы значений переменных, на которых формула принимает значение 1(=1):

{(0011),(0100),(0101),(0110),(0111),(1011),(1111)}. Теперь применяем правило, по которому СДНФ функции содержит столько конъюнкт, сколько единиц в столбце значений ; каждому единичному набору нулей и единиц соответствует конъюнкта всех переменных, в которых взято с отрицанием, если , и без отрицания, если. Итак, СДНФ нашей формулы содержит дизъюнкцию семи конъюнкт вида (знак опустим):

;

г) карта Карно функции четырёх переменных представляет собой таблицу, содержащую ячеек (столько, сколько всех возможных наборов 0 и 1 функции четырёх переменных), строки и столбцы соответствуют значениям переменных или их отрицаниям, так, чтобы соседние ячейки отличались только значением одной переменной. Для получения МДНФ каждая конъюнкта СДНФ функции отмечается единицей в соответствующей ячейке карты Карно;

	1			1
	1	1
	1	1		1

Рисунок 1

д) чтобы получить МДНФ, надо объединить рядом стоящие по вертикали и горизонтали единицы в так называемые блоки, состоящие из 2, 4, 8 и т.д. ячеек (блоком из 2 ячеек считаются также единицы, стоящие в углах при одной стороне таблицы или из 4 – единицы, стоящие во всех углах, т.к., например, в последнем случае карту можно «свернуть» как тор столбцы к столбцам (С к С) и строки к строкам (D к D)). В нашей карте Карно есть два блока по 4 ячейки. Блок, стоящий в левом нижнем углу покрывают переменные и , поэтому ему соответствует конъюнкция , блоку из 4 ячеек в углах карты соответствует конъюнкция . Таким образом, МДНФ формулы имеет вид .

е) приведём МДНФ к конъюнктивной нормальной форме (КНФ):

=[двойное отрицание]==

[закон Де-Морганаъюнктивной нормальной форме (КНФ):

нем углу покрывают переменные ]==[закон Де-Морганаъюнктивной нормальной форме (КНФ):

нем углу покрывают переменные ]=

==[дистрибутивность]=

==[закон Де-Морганаъюнктивной нормальной форме (КНФ):

нем углу покрывают переменные ]=

==[закон Де-Моргана, двойное отрицаниеъюнктивной нормальной форме (КНФ):

нем углу покрывают переменные ]=

= - КНФ формулы;

ж) совершенную конъюнктивную нормальную форму (СКНФ) получим используя нулевые наборы значений переменных. Выпишем из таблицы истинности формулы наборы, на которых формула имеет значение 0 (=0):

. Теперь, следуя правилу, что СКНФ содержит столько дизъюнкт, сколько нулей в столбце значений , и каждому нулевому набору нулей и единиц соответствует дизъюнкта всех переменных, в которых i-ая переменная взята с отрицанием, если , и без отрицания, если , получим; –

СКНФ формулы;

з) для получения МКНФ можно использовать карту Карно, по которой минимизировали ДНФ, заменив в ней переменные на их отрицания и наоборот, на пустые места поставив 0 и убрав 1, либо заполнить нулями ячейки соответствующие дизъюнктам СКНФ. Отметим на карте максимальные блоки, содержащие 2,4,8 и т.д. нулевых соседних ячеек. В нашем случае имеется 4 блока по 4 ячейки, которым соответствуют упрощённые дизъюнкты двух переменных. Окончательно получим, что МКНФ формулы имеют вид

.

		0	0
	0	0	0	0
			0	0
			0

Рисунок 2

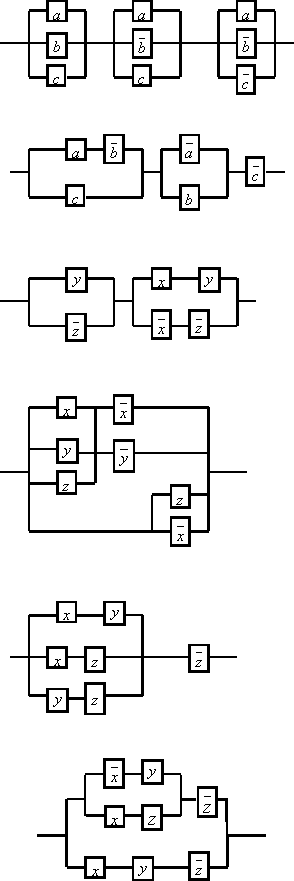
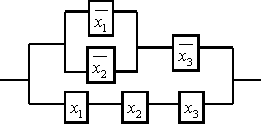
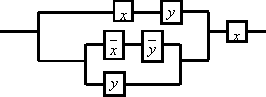
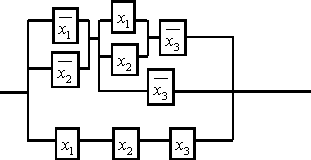4 Упростить схему

Решение:

составим функцию проводимости для данной схемы

. Используя один из методов ( например, метод элементарных преобразований, минимизация с помощью карт Карно и т.д.), упрощаем эту функцию:

[дистрибутивность]==[свойство поглощения]=

=. Полученной формуле соответствует упрощённая схема:

1.4 Справочный материал

Логические операции и их таблицы истинности

1. Конъюнкция – (), читается «x и y».

2. Дизъюнкция – ( ), читается «x или y».

3. Отрицание (инверсия) – (), читается «не x».

4. Импликация - (), читается «если х, то у».

5. Эквиваленция – (), читается «х если и только если у».

6. Штрих Шеффера – (), определяется как отрицание конъюнкции, т.е. читается «не x и y».

7. Стрелка Пирса – (), определяется как отрицание дизъюнкции, т.е. читается «не x или y».

8. Кольцевая сумма – (), определяется как отрицание эквиваленции (исключающее «или»), т.е. читается «или х, или у».

0	0	1	0	0	1	1	1	1	0
0	1		0	1	1	0	1	0	1
1	0	0	0	1	0	0	1	0	1
1	1		1	1	1	1	0	0	0

Основные эквивалентные соотношения (законы)

1	Коммутативность
2	Ассоциативность
3	Дистрибутивность
4	Идемпотентность
5	Законы поглощения
6	Закон Де-Моргана
7	Двойное отрицание
8	Свойства констант
9	-закон противоречия		-закон исключённого третьего

Некоторые другие полезные эквивалентные соотношения:

10	Закон склеивания
10а	Закон расщепления
11	Обобщённое склеивание
12
13
14
15
16

Схема приоритетов логических операций

Список литературы

1. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2002.

2. Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учебное пособие. – М.: Логос, 2004. – 240 с.

3. Новиков Ф.А. Дискретная математика для программистов: Учебник для вузов. 2-е изд. – СПб.: Питер, 2004. – 364 с.: ил. – (Серия «Учебник для вузов»).

4. Андерсон Д. Дискретная математика и комбинаторика.: Пер. с англ. – М.: Издатель- ский дом «Вильямс», 2004. – 960 с.: ил. – Парал. тит. англ.

5. Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. – СПб.: БХВ-Петербург, 2006.

6. Яблонский С.В. Введение в дискретную математику. – М. «Высшая школа», 2001.

Содержание

1 Типовой расчёт 2. Математическая логика