
Счисления
.pdfОсновные понятия и определения
Система счисления – совокупность приемов и правил записи чисел с помощью определенного набора знаков. Набор знаков называется алфавитом системы счисления. В качестве условных знаков для записи чисел используются цифры. Если цифр недостаточно, то используются буквы латинского алфавита, например, А, В, С и т.д.
Системы счисления бывают позиционные и непозиционные.
Система счисления, в которой значение каждого символа в записи числа не зависит от того места, на котором он стоит, называется непозиционной. Хорошо известным примером непозиционной системы счисления является римская система, в которой роль символов играют буквы латинского алфавита: І – один, V – пять, Х – десять, С – сто, L – пятьдесят, D – пятьсот, М – тысяча.
Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается от большей, если справа - прибавляется.
Примеры.
1. Десятичное число 88 в римской системе счисления имеет вид LXXXVIII. Символ X в записи числа встречается три раза и означает одну и ту же величину – десять единиц. Количественное значение числа определяется следующим образом:
LXXXVIII = 50 +10 + 10 + 10 + 5 + 1 + 1 + 1 = 8810.
2. Запись десятичного числа 1999 в римской системе счисления будет иметь вид:
МСМХСIХ = 1000 + (1000 - 100) + (100 -10)+ (10 -1) = 199910.
В непозиционных системах не представлены дробные и отрицательные числа, а арифметические операции выполнять неудобно и сложно. В математической практике они не используются, но нашли применение в циферблатах часов, при оформлении списков и др.
Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, то есть в ней использовалось шестьдесят цифр. И в наши дни при измерении времени мы используем основание, равное 60.
Примеры.
1 минута = 60 секундам.
1 час = 60 минутам.
1 градус = 60 минутам.
В XIX веке широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем слово
3
дюжина (число 12), остатки двенадцатеричной системы счисления имеются и у англичан.
Примеры.
В сутках две дюжины часов.
Круг содержит тридцать дюжин градусов. 1 фут = 12 дюймам.
1 шиллинг = 12 пенсам.
В настоящее время наиболее распространенными позиционными системами счисления являются десятичная, двоичная, восьме-
ричная и шестнадцатеричная.
В позиционных системах счисления количественное значение числа зависит от цифры и от места (позиции), которое занимает цифра в числе. Современная десятичная системы счисления (арабская), использующая цифры от 0 до 9, является позиционной.
Пример. В числе 127:
1 – количество сотен;
2 – количество десятков;
7 – количество единиц.
Если записать цифры в другой последовательности, например, 721, то получим другое количественное значение. В числе 721:
7 – количество сотен;
2 – количество десятков;
1 – количество единиц. Преимущество позиционных систем:
a)позволяют записывать большие числа с помощью небольшого числа знаков;
b)просто и легко выполнять арифметические операции над чис-
лами.
Основные характеристики позиционной системы счисления – база
иоснование. База – это сами символы (цифры), а основание – количество символов (цифр), используемых для записи любого числа в данной системе счисления. Количество цифр в алфавите еще называют мощностью алфавита. Основание означает, во сколько раз единица
следующего разряда больше чем единица предыдущего разряда. При записи чисел в позиционных системах счисления принято записывать основание справа внизу числа (нижний индекс).
Пример. Число 10111 в двоичной системе счисления будет запи-
сано: 101112.
Две системы называются родственными, если основание одной системы счисления равно степени основания другой.
Примеры.
1.Двоичная и восьмеричная (23 = 8).
2.Двоичная и шестнадцатеричная (24 = 16).
3.Троичная и девятеричная (32 = 9).
4
Любое число N в позиционной системе можно записать в виде
суммы степеней основания р с соответствующими коэффициентами:
Np = anpn + an-1pn-1 + an-2pn-2 … + а0р0 + а -1р-1 +а -2р-2 +… а -nр-n,
Коэффициенты при степенях – цифры от 1 до р-1. Каждый коэффициент принимает только положительные значения и называется весом i-го разряда. Показатель степени – номер позиции цифры в записи числа Нумерация показателя степени для целой части числа ведется справа налево, начиная с 0, а для дробной – слева направо, начиная с 1.
Примеры.
1.Число 1236, записанное в семеричной системе счисления,
можно записать по степеням основания 7:
12367 = 1*73 + 2*72 +3*71 + 6*70.
2.Число 1236,235, записанное в десятичной системе, можно раз-
ложить по степеням основания 10:
1236,23510 = 1*103 + 2*102 + 3*101 + 6*100 + 2*10-1 + 3*10-2 + 5*10-3 .
Для десятичной системы счисления понятие веса соответствует общепринятым названиям позиций - единицы, десятки, сотни и т.д. для целой части числа и десятые доли, сотые доли и т.д. для дробной части.
Арифметические операции (сложение, умножение и др.) в позиционной системе выполняют по правилам. Например, при сложении двух многозначных чисел, применяется правило сложения «столбиком». При этом все сводится к сложению однозначных чисел, для которых необходимо знать таблицу сложения. Когда при сложении в предыдущем разряде получается сумма, значение которой больше чем р - 1 (р - ос-
нование той системы счисления, в которой выполняется суммирование), надо сделать перенос младшей единицы в старший разряд.
Для деления многозначных чисел применяется правило «угла».
Правила перевода целых чисел
Для перевода целых чисел из десятичной системы счисление в другую позиционную систему необходимо выполнить следующие ниже действия:
1.Разделить исходное число на новое основание.
2.Записать частное и остаток.
3.Полученное частное снова разделить на основание. Деление выполнять до тех пор, пока частное не станет равным нулю.
4.Полученные остатки, записанные в обратном порядке, дадут искомое число.
Для перевода целого числа из любой системы счисления с основанием р в десятичную систему необходимо:
1. Расписать число по степеням основания р.
5
2. Выполнить арифметические действия (возведение в степень и сложение) в десятичной системе счисления.
Перевод целого числа всегда является конечным процессом.
Правила перевода правильных дробей
1.Умножить исходное число на новое основание р.
2.Выделить целую и дробную части произведения. Целая часть даст первую цифру после запятой в искомой дроби.
3.Новую дробную часть снова умножить на основание р.
4.Очередная целая часть произведения даст вторую цифру после запятой в искомой дроби. Перейти к пункту 3.
5.Процесс перевода заканчивается в двух случаях:
a)дробная часть некоторого произведения равна 0;
b)достигнута заданная точность перевода.
Правила перевода неправильных дробей
Для перевода неправильной дроби из одной системы счисления в другую, нужно отдельно перевести целую и дробную части по соответствующим правилам, затем к новой целой части числа после запятой приписать дробную часть.
Двоичная система счисления
В вычислительной технике широко применяют самую простую позиционную систему счисления двоичную, в которой для изображения числа требуется только две цифры: 0 и 1. Вся информацию (числовая, текстовая, графическая, звуковая, видео) представлена в памяти компьютера в двоичном коде. Эта система близка к оптимальной по экономичности, и кроме того, таблицы сложения и умножения в этой системе элементарные.
Для двоичной системы счисления:
основание – 2 (210 = 102). база – 0,1.
6

Примеры.
1. Перевести число 2510 в двоичную систему счисления.
Способ 1. Деление на новое основание 2 выполним «углом»:
Остатки |
25 |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
12 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Получили: 2510 = 110012.
Способ 2. Для перевода целых чисел из десятичной системы счисления в двоичную и обратно, надо выучить таблицу первых десяти степеней числа 2:
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
2n |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
|
|
|
|
|
|
|
|
|
|
|
|
Разложим число 25 на степени числа 2:
25 = 16 + 8 +1 = 1*24 + 1*23 + 1*20 = 1*24 + 1*23 + 0*22 +0*20 + 1*20.
Выписав двоичные цифры, стоящие перед степенями, получим:
2510 = 1100112.
2. Перевести число 1100112 в десятичную систему счисления.
Способ 1. Распишем число по степеням основания 2 и выполним арифметические действия. Так как цифр в исходном числе 6, то начнем с показателя n = 5:
1100112 = 1*25 + 1*24 + 0*23 +0*22 + 1*21 + 1*20 = 32 + 16 + 0 + 0 +2 +
1 = 5110.
1100112 = 5110.
7
Способ 2. Пронумеруем цифры числа справа налево, начиная с нуля, подпишем под ненулевыми разрядами соответствующие степени двойки и выполним суммирование:
Исходное число |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
Номер цифры |
5 |
4 |
3 |
2 |
1 |
0 |
|
|
|
|
|
|
|
Степени числа 2 |
32 |
16 |
|
|
2 |
1 |
|
|
|
|
|
|
|
1100112 = 32 + 16 + 2 +1= 5110.
3. Перевести число 0,12510 в двоичную систему счисления.
Имеем правильную дробь, поэтому умножим дробную часть на основание 2. Умножение выполним 3 раза.
|
х |
0,125 |
х |
0,250 |
х |
0,5 |
|
2 |
2 |
2 |
|||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0,250 |
|
0,50 |
|
1,0 |
|
|
|||||
|
Цифры после запятой в двоичном числе |
|||||
|
|
|
|
|
|
|
0, |
|
0 |
|
0 |
|
1 |
В результате перевода получили конечную двоичную дробь:
0,12510 = 0,0012.
4. Перевести число 0,210 в двоичную систему счисления с точностью 0,00000001.
х |
0,2 |
х |
0,4 |
х |
0,8 |
х |
0,6 |
х |
0,2 |
|
2 |
2 |
2 |
2 |
2 |
||||||
|
|
|
|
|
||||||
|
0,4 |
|
0,8 |
|
1,6 |
|
1,2 |
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
Цифры |
|
|
|
|
|
|
|
|
|
|
после |
0 |
|
0 |
|
1 |
|
1 |
|
0 |
|
запятой: |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
После четвертого шага умножения цифры в целой части результата умножения начинают повторяться, т.е. получили бесконечную периодическую двоичную дробь.
Результат перевода: 0,210 0,001100112.
5. Перевести число 25,210 в двоичную систему счисления с точностью 0,00001.
Переведем отдельно целую и дробную части числа:
8

2510 = 110012, |
0,210 0,001102 |
|
Результат перевода: |
25,210 11001,001102. |
|
6. Перевести число 1100,112 в десятичную систему счисле-
ния.
Распишем исходное число по степеням основания 2. Так как в записи целой части числа равно 4 цифры, то начнем расписывать с показателя n = 3:
1100,112 = 1*23 + 1*22 + 0*21 +0*20 + 1*2-1 + 1*2-2 = 8 + 4 + 0 + 0 +1/2 + 1/4 = 12 + 0,5 + 0,25 = 12,7510.
1100,112 = 12,7510.
7. Найти сумму двоичных чисел 10101012 и 1011112.
Сложение многозначных двоичных чисел происходит в соответствии с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов в старшие.
Запишем одно число под другим и выполним суммирование столбиком, учитывая, что две единицы младшего разряда образуют единицу старшего (12 +12 = 102).
Переносимые единицы |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
Первое слагаемое |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
Второе слагаемое |
|
|
1 |
0 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
Сумма |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
Результат сложения: 10101012 + 1011112 =100001002.
Проверим правильность выполнения сложения, переведя исходные двоичные числа и полученную сумму в десятичную систему счисления:
10101012 = 1*26 + 1*24 + 1*22 +1*20 = 64 + 16 + 4 + 1 = 8510. 1011112 = 32 + 8 + 4 + 2 + 1 = 4710.
100001002 = 128 + 4 = 13210.
8510 + 4710 = 13210.
Сумма найдена правильно.
8. Найти сумму двоичных чисел 10101,012 и 10,11112.
10101,01 + 10,111
11000,0011
10101,012 + 10,11112 = 11000,00112.
9

Восьмеричная система счисления
Двоичная система, являющаяся основой всей компьютерной арифметики, очень громоздка и неудобна для использования человеком. Поэтому программисты пользуются двумя родственными систе-
мами счисления: восьмеричной и шестнадцатеричной.
Для восьмеричной системы счисления:
база – 0, 1, 2, 3, 4, 5, 6, 7;
основание – 8.
Таблица сложения восьмеричных чисел
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
|
|
|
|
|
|
|
|
|
2 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
|
|
|
|
|
|
|
|
|
3 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
|
|
|
|
|
|
|
|
|
4 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
|
|
|
|
|
|
|
|
|
5 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
|
|
|
|
|
|
|
|
|
6 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
|
|
|
|
|
|
7 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
|
|
|
|
|
|
|
Чтобы заполнить таблицу, переведем каждое слагаемое в десятичную систему, найдем сумму, которую распишем по степеням основания 8.
Например, 58 + 78 = 510 + 710 = 1210 = (8 + 4)10 = 1*81 +4*80 = 148.
Получили: 58 + 78 = 148.
Так как двоичная и восьмеричная системы счисления являются родственными, то перевод из одной в другую можно осуществить напрямую, воспользовавшись таблицей связи, где каждая восьмеричная цифра расписана как три двоичных.
10
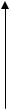
Восьмеричное |
Двоичное |
число |
число |
0 |
000 |
|
|
1 |
001 |
|
|
2 |
010 |
|
|
3 |
011 |
|
|
4 |
100 |
|
|
5 |
101 |
|
|
6 |
110 |
|
|
7 |
111 |
|
|
Примеры.
1. Перевести число 73510 в восьмеричную систему.
Разделим исходное число на основание 8. Деление выполним, используя правило «угла», запоминая на каждом шаге частное и остаток:
Остатки |
735 |
8 |
|
|
|
|
|
|
|
|
|
7 |
|
91 |
8 |
|
|
|
|
|
|
|
|
3 |
|
|
11 |
8 |
|
|
|
|
|
|
|
3 |
|
|
|
1 |
8 |
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
Остатки, прочитанные в обратном порядке, дают искомое число:
73510 = 13378.
Проверим правильность перевода, расписав полученное восьмеричное число по степеням основания 8:
13378 = 1*83 + 3*82 + 3*81 + 7* 80 = 1*256+3*64 +3*8 +7*1 = 512 + 192
+24 + 7 = 73510.
2.Найти сумму восьмеричных чисел 76278 и 7548.
11

Запишем одно число под другим и выполним суммирование столбиком, перенося единицу в старший разряд, если сумма цифр в младшем разряде равна или больше основания 8 (78 +18=108):
Переносимые единицы |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
Первое слагаемое |
|
7 |
6 |
2 |
7 |
|
|
|
|
|
|
Второе слагаемое |
|
|
7 |
5 |
4 |
|
|
|
|
|
|
Сумма |
1 |
0 |
6 |
0 |
3 |
|
|
|
|
|
|
Результат сложения: 76278 + 7548 = 106038.
3. Найти сумму восьмеричных чисел 76,278 и 7,548.
Выполним сложение «столбиком»:
126,24 + 7,54 136,00
76,278 + 7,548 = 136,0 08
4. Перевести число 1548 в двоичную систему счисления.
Воспользуемся таблицей связи двух родственных систем и распишем каждую восьмеричную цифру как три двоичных, затем отбросим слева незначащие нули.
1548 = 001 101 1002 = 11011002.
1548 = 11011002.
5. Перевести число 100010011102 в восьмеричную систему счисления.
Сгруппируем справа налево разряды исходного числа по три цифры, т.е. разобьем на триады. Если левая группа цифр будет неполной триадой, то дополним ее слева нулями. Заменим каждую триаду соответствующей цифрой восьмеричной системы счисления, воспользовавшись таблицей связи двух систем.
100010011102 = 10 001 001 1102= 010 001 001 1102 = 21168.
100010011102 = 21168.
6. Перевести число 1000,10011102 в восьмеричную систему счисления.
Разобьем число на триады целую часть справа налево, а дробную слева направо. Добавим недостающие нули в неполные крайние триады и каждую триаду заменим восьмеричной цифрой.
1001100,100110001102 = 1 001 100,100 110 001 10 =
= 001 001 100,100 110 001 100 = 114,45148.
12
