Л-я вышмат 8-9

Лекция 8-9

Числовые ряды

Вопросы

1. Дайте определение числового ряда.

2. Что называется суммой числового ряда?

3. Дайте определение сходимости числового ряда.

4. В чем заключается необходимый признак сходимости числового ряда?

5. Приведите пример числового ряда, для которого необходимый признак выполняется, но, тем не менее, ряд расходится.

6. Знакоположительные ряды.

7. Какие достаточные признаки сходимости вы знаете?

1. Числовые ряды. Сходимость и сумма рядов

Необходимый признак сходимости. Свойства сходящихся рядов.

Понятие ряда означает нахождение суммы бесконечного числа слагаемых. Хотя такую сумму путем непосредственного сложения подсчитать невозможно, ее приближенное значение, взяв большое число слагаемых, казалось бы, несложно получить с помощью компьютера. Но это не совсем так. Теория рядов необходима для того, чтобы прежде всего установить имеет ли данный ряд конечную сумму и, в случае положительного ответа, определить количество слагаемых, которое необходимо взять для того, чтобы найти эту сумму ряда с требуемой точностью.

1. Определение. Выражение вида

или, подробнее, (10.1)

называется числовым рядом, числа называются его членами.

Для определенности будем считать первым членом ряда, хотя ряд может начинаться и с любого другого члена.

Сумма первых слагаемых ряда (10.1) называется его частичной суммой, она обозначается через . При этом

,

,

,

................................

.

Определение. Если существует конечный предел частичных сумм ряда (10.1) при , то это число называется суммой ряда , а ряд в этом случае называется сходящимся: .

Если предел частичных сумм не существует (например, равен ),то ряд называется расходящимся. У расходящегося ряда сумма не определена.

Пример1. Рассмотрим ряд, изучаемый в школьной программе – геометрическую прогрессию.

Это ряд вида: .

Здесь - первый член геометрической прогрессии, а называется ее знаменателем.

Частичная сумма геометрической прогрессии определяется формулой

.

Если и , то и геометрическая прогрессия расходится.

Если и , то , и геометрическая прогрессия расходится.

Если и , то

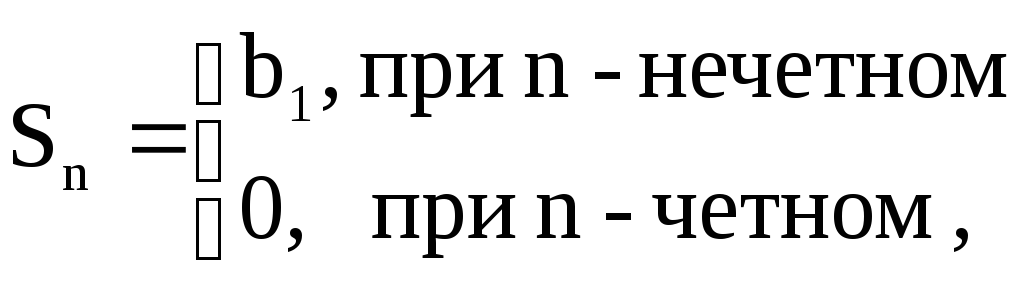
не существует и прогрессия расходится. Итак, при геометрическая прогрессия сходится только при .

При геометрическая прогрессия всегда сходится.

2. Рассмотрим теперь простейшие свойства рядов.

1. Пусть числовые ряды

(10.1)

и

(10.2)

сходятся, и имеют суммы соответственно и , тогда ряд

(10.3)

также сходится и его сумма равна .

2)Если ряд (10.1) сходится, число , то ряд

(10.4)

также сходится и его сумма равна .

Если же ряд (10.1) расходится и , то ряд (10.4) расходится.

Это свойство означает, что постоянный множитель можно выносить из всех членов сходящегося ряда.

3) Если в ряде (10.1) изменить, добавить или отбросить конечное число членов, то сходимость этого ряда не изменится, т.е. если ряд (10.1) сходился, то новый ряд также сходится, а если ряд (10.1) расходился, то новый ряд расходится.

Пример2. Так как ряд

сходится (это геометрическая прогрессия с ), то ряд

также сходится.

Теорема 1. (Необходимый признак сходимости). Если ряд

сходится, то предел его членов при равен ; т.е. .

Доказательство. Поскольку последовательность частичных сумм ряда сходится, то

и .

Вычитая из первого соотношения второе получим

, т.е.

что и требовалось доказать.

Условие является только необходимым, оно не является достаточным для сходимости ряда. Об этом свидетельствует пример гармонического ряда

.

Как будет проверено в дальнейшем, этот ряд является расходящимся, хотя у него

.

Поэтому с помощью необходимого признака невозможно установить сходимость ряда. Чаще применяется обратное утверждение, равносильное доказанной теореме.

Следствие. Если не равен нулю, то ряд (10.1) расходится.

Пример3. Рассмотрим ряд

Найдем предел его членов.

Поскольку он не равен нулю, то записанный ряд расходится.

2.Достаточные признаки сходимости для рядов

с положительными членами

Теорема 2. (Первый признак сравнения). Пусть имеется два ряда

(10.1)

и

(10.2)

с положительными членами , удовлетворяющими неравенству

(10.5)

для всех, за исключением, быть может, конечного числа членов рядов.

Тогда если ряд (10.2) сходится, то ряд (10.1) также сходится, если же ряд (10.1) расходится, то ряд (10.2) также расходится.

Пример4. Исследуем сходимость ряда

.

Для сравнения используем расходящийся гармонический ряд

.

При и ,

поэтому, согласно первому признаку сравнения, исследуемый ряд расходится.

Для сравнения обычно используют такие известные ряды как геометрическая прогрессия или ряд Дирихле.

Рядом Дирихле называется числовой ряд вида

.

Немного позже мы докажем, что ряд Дирихле при сходится, а при расходится. При от превращается в гармонический ряд.

Пример5. Исследуем сходимость ряда

.

Для сравнения возьмем сходящийся ряд Дирихле

.

(Здесь ). Поскольку , то для всех .

И исследуемый ряд сходится.

Теорема 3. (Предельный признак сравнения).

Пусть ряды

(10.1)

и

(10.2)

с положительными членами таковы, что существует конечный ненулевой предел

.

Тогда ряды (10.1) и (10.2) сходятся или расходятся одновременно.

Пример. Исследуем сходимость ряда

.

Для сравнения подберем ряд Дирихле следующим образом. Оставив в числителе и знаменателе слагаемые с наибольшей степенью, получим ряд с членами

,

которые составляют сходящийся ряд Дирихле с параметром .

Найдем число .

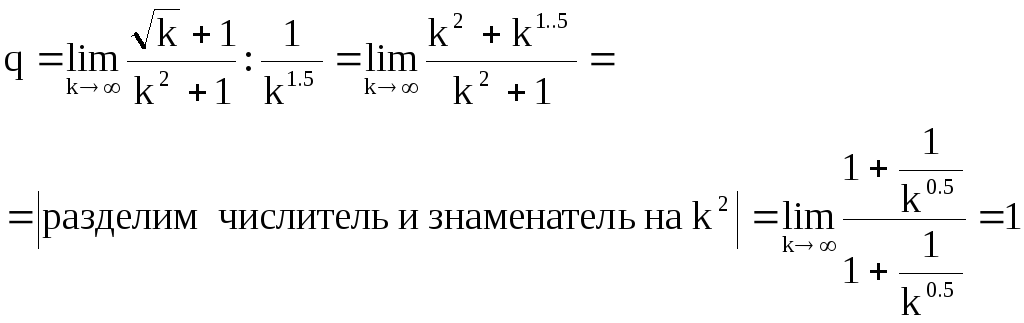
Итак, согласно предельному признаку, исследуемый ряд сходится.

Теорема 4. (Признак Даламбера)

Пусть у ряда

где существует предел отношений

, (10.6)

тогда:

а) если , то этот ряд сходится,

в) если или этот ряд расходится.

При данный признак не применим.

Пример7. Исследуем сходимость ряда .

Для этого ряда , поэтому

,

т.к. , то исследуемый ряд сходится.

Теорема 5. (Радикальный признак Коши). Пусть в ряде ,

где , существует предел

. (10.7)

Тогда:

а) если , то этот ряд сходится,

в) если или ,то этот ряд расходится.

При , как и в предыдущем случае, признак Коши не применим.

Пример8. Исследуем сходимость ряда

.

Вычислим требуемый предел.

. (Второй замечательный предел). Поскольку , то исходный ряд сходится.

Теорема 6. (Интегральный признак Коши).

Пусть имеется ряд

(10.1)

и несобственный интеграл

, (10.9)

такие, что выполняются следующие условия:

а) для целых

,

б) функция непрерывна, неотрицательна и не возрастает на промежутке .

Тогда ряд (10.1) и интеграл (10.9) сходятся или расходятся одновременно.

Доказательство можно продемонстрировать на рисунке 10.

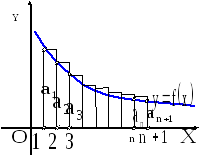
Рис. 10

Пример 9. Исследуем сходимость ряда Дирихле для различных :

.

Функция получается путем замены индекса суммирования на . При она удовлетворяет всем условиям теоремы. Она непрерывна, в промежутке , т.к. имеет разрыв только в точке в этом промежутке и убывает в нем, т.к. ее знаменатель возрастает с ростом .

Пусть, тогда

,

т.е. при этот интеграл и ряд Дирихле сходятся.

При этот интеграл и ряд Дирихле расходятся.

При

.

Заметим, что при члены ряда Дирихле не стремятся к нулю, поэтому он расходится согласно следствию из необходимого признака.

Следствие. Интегральный признак можно применять и к рядам вида

.

В этом случае условия, накладываемые на функцию должны выполняться на промежутке .

Интегральный признак следует применять в тех случаях, когда возможно интегрирование функции .

Пример10. Исследуем сходимость ряда

.

Понятно, что член этого ряда по написанной формуле определить не- возможно.

Элементарная функция определена в промежутке , поэтому она непрерывна в промежутке , положительна в нем и убывает, т.к. ее знаменатель возрастает с ростом .

Найдем несобственный интеграл

.

Т.е. исследуемый ряд расходится.

Литература

1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление, М.:Наука, 1988г.

2. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.1,2 М.:Наука, 1985г.

3. Кудрявцев Л.Д. Курс математического анализа. Т. 1,2, М.: Высшая школа, 1981г.

4. Бронштейн И.Н.,Семендяев К.А. Справочник по математике для инженеров.М.: Высшая школа,1997 .

5. ИДЗ. Дифференциальное исчисление функции одной переменной. Под редакцией Рябушко А.П., ч.1,2 Минск, «ВШ», 2002г.