
- •1. С помощью алгоритма Дейкстры найти путь минимального веса между вершинами s и t в нагруженном графе.
- •Решение
- •2. Найти максимальный поток в заданной транспортной сети, используя алгоритм Форда-Фалкерсона. Проверить ответ по теореме Форда-Фалкерсона (найти минимальный разрез графа сети).
- •Решение
- •3. По матрице инцидентности построить остовное дерево графа. Составить список ветвей и хорд графа. Построить граф.
- •Решение
- •4. А) Написать таблицу состояний данного автомата.


1. С помощью алгоритма Дейкстры найти путь минимального веса между вершинами s и t в нагруженном графе.
Решение
Прямого пути из вершины ![]() в вершину
в вершину ![]() нет. Поэтому применим алгоритм Дейкстры.
нет. Поэтому применим алгоритм Дейкстры.
Вершине ![]() присваиваем метку 0. Все остальные
вершины имеют метки
присваиваем метку 0. Все остальные
вершины имеют метки ![]() .
Из вершины
.
Из вершины ![]() можно напрямую попасть в вершины
можно напрямую попасть в вершины ![]() и
и ![]() .
Это кратчайшие расстояния, поэтому
метки этих вершин заменяем соответствующими
весами графа (зелёный цвет). Вершина
.
Это кратчайшие расстояния, поэтому
метки этих вершин заменяем соответствующими
весами графа (зелёный цвет). Вершина ![]() считается посещённой, поэтому вычёркиваем
её. Получим:
считается посещённой, поэтому вычёркиваем
её. Получим:
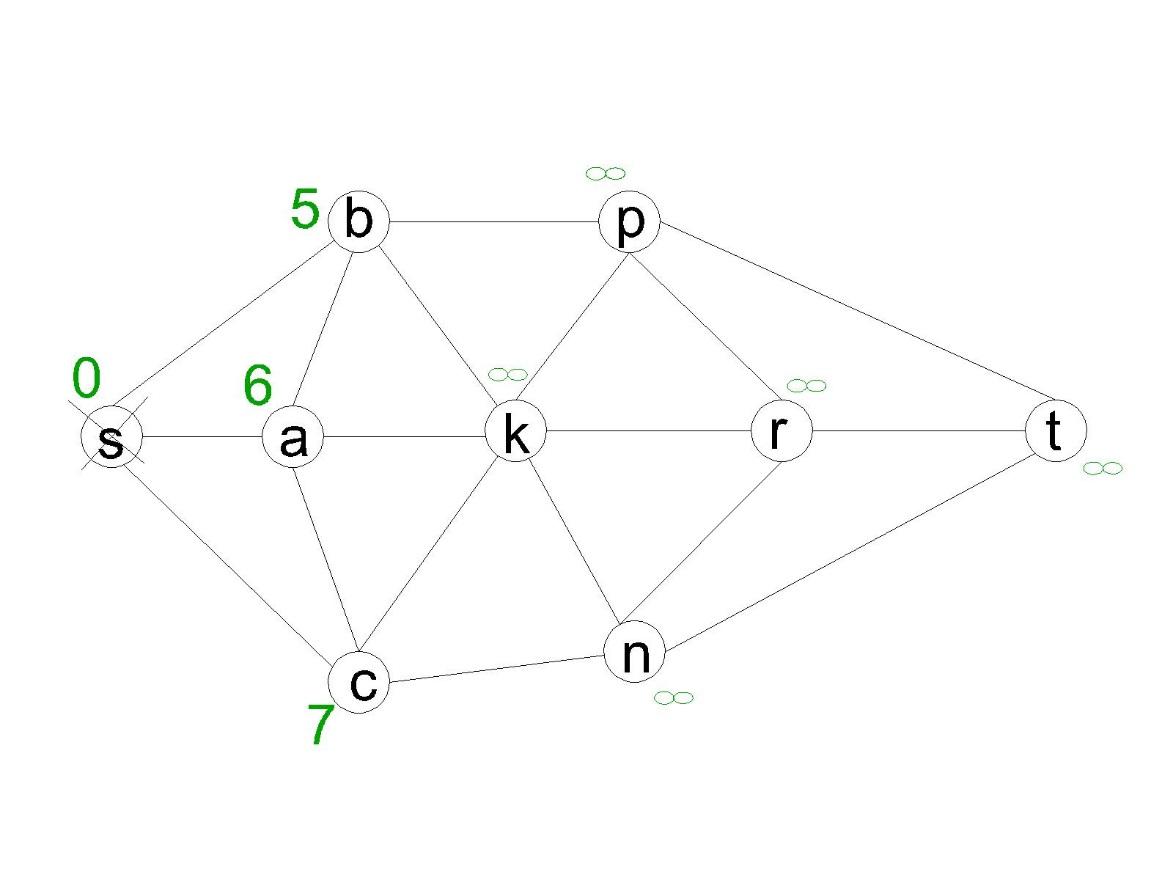
Ближайшая из непосещённых вершин –
вершина ![]() .
Из неё можно попасть в вершины
.
Из неё можно попасть в вершины ![]() и
и ![]() .
Путь в вершину
.
Путь в вершину ![]() будет
равен
будет
равен ![]() (
(![]() – путь из вершины
– путь из вершины ![]() в вершину
в вершину ![]() ,
,
![]() – путь из вершины
– путь из вершины ![]() в вершину
в вершину ![]() ).
).
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() будет равен
будет равен ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]()
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() будет равен
будет равен ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]() ).
). ![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() станет равен
станет равен ![]() .
Вершина
.
Вершина ![]() становится посещённой, поэтому вычёркиваем
её. Получим:
становится посещённой, поэтому вычёркиваем
её. Получим:
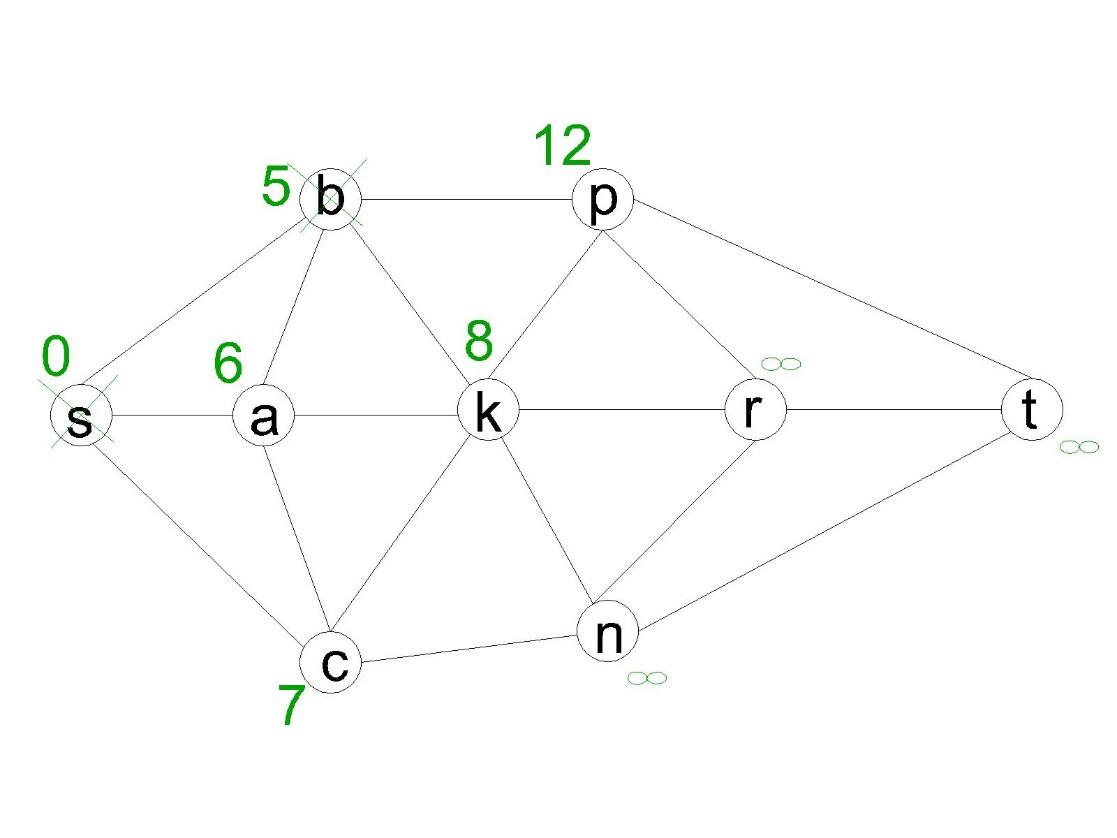
Ближайшая из непосещённых вершин –
вершина ![]() .
Из неё можно попасть в вершины
.
Из неё можно попасть в вершины ![]() и
и ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]() .
.
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() останется равным
останется равным ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]()
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() будет равен
будет равен ![]() .
Вершина
.
Вершина ![]() становится посещённой, поэтому вычёркиваем
её. Получим:
становится посещённой, поэтому вычёркиваем
её. Получим:
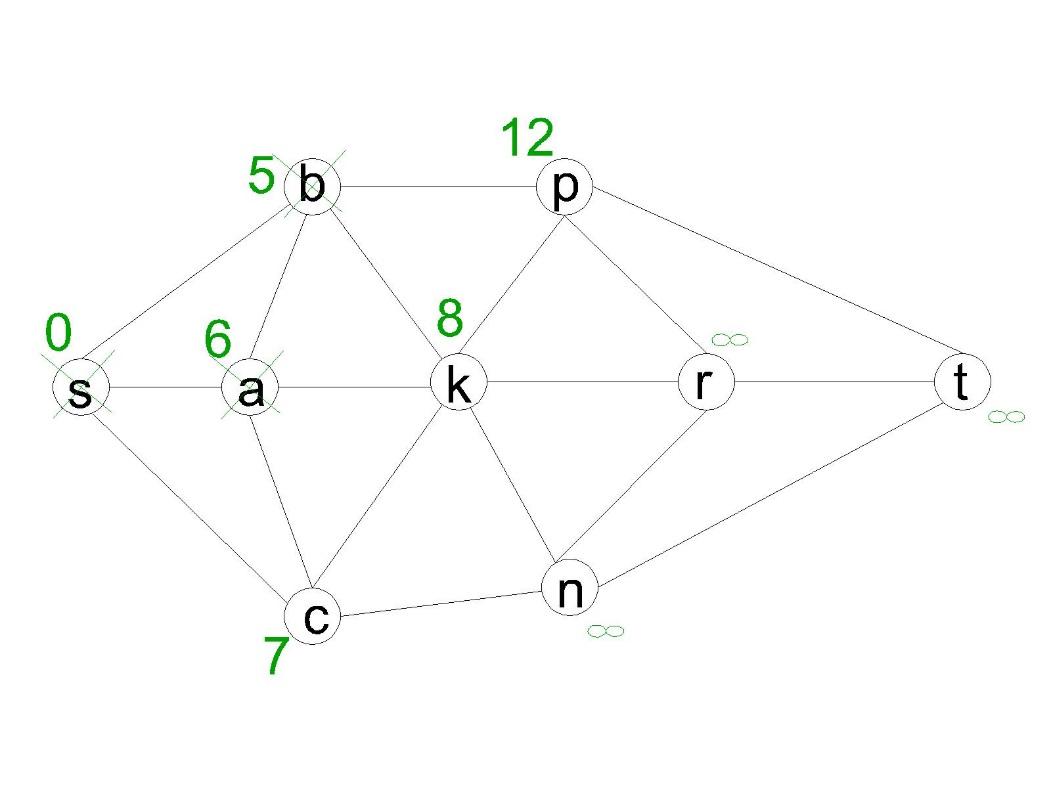
Ближайшая из непосещённых вершин –
вершина ![]() .
Из неё можно попасть в вершины
.
Из неё можно попасть в вершины ![]() и
и ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]()
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() останется равным
останется равным ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]() ).
). ![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() станет равен
станет равен ![]() .
Вершина
.
Вершина ![]() становится посещённой, поэтому вычёркиваем
её. Получим:
становится посещённой, поэтому вычёркиваем
её. Получим:
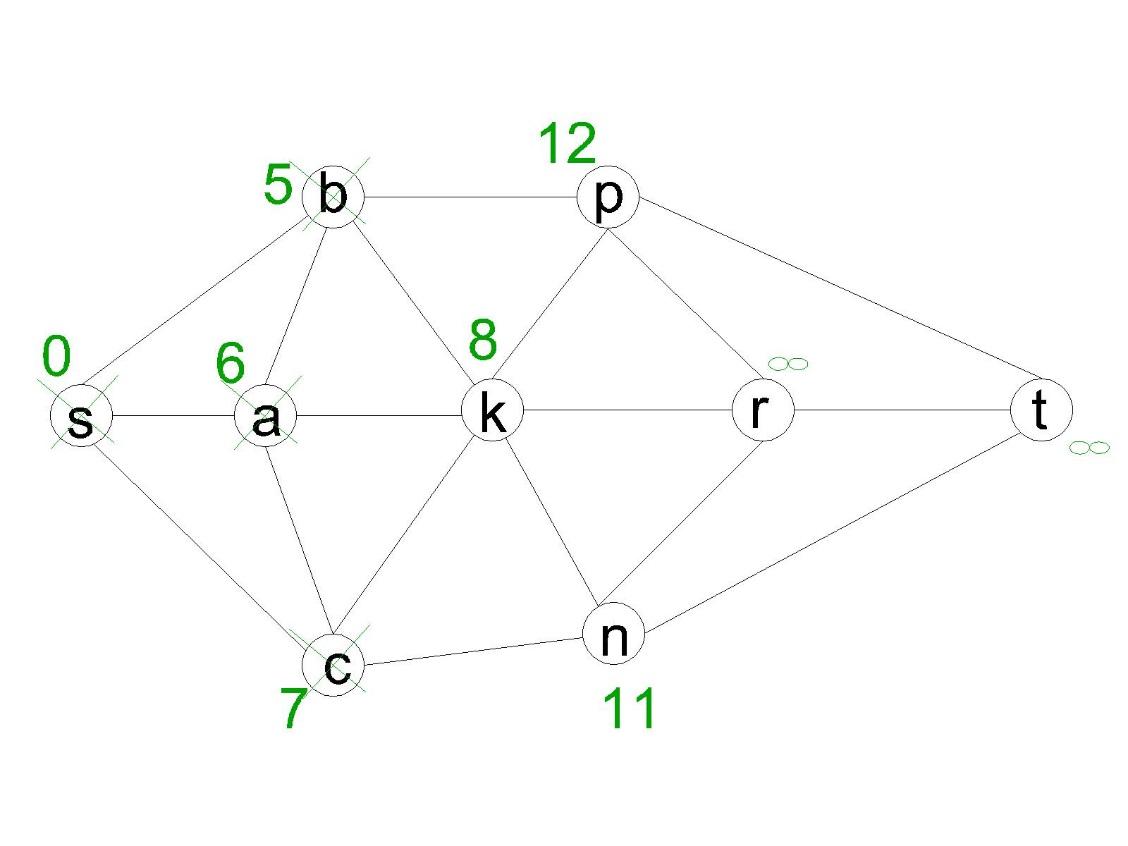
Ближайшая из непосещённых вершин –
вершина ![]() .
Из неё можно попасть в вершины
.
Из неё можно попасть в вершины ![]() и
и ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]() .
.
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() станет равен
станет равен ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]()
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() будет равен
будет равен ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]() ).
). ![]() поэтому вес вершины
поэтому вес вершины ![]() останется равным
останется равным ![]() .
Вершина
.
Вершина ![]() становится посещённой, поэтому вычёркиваем
её. Получим:
становится посещённой, поэтому вычёркиваем
её. Получим:
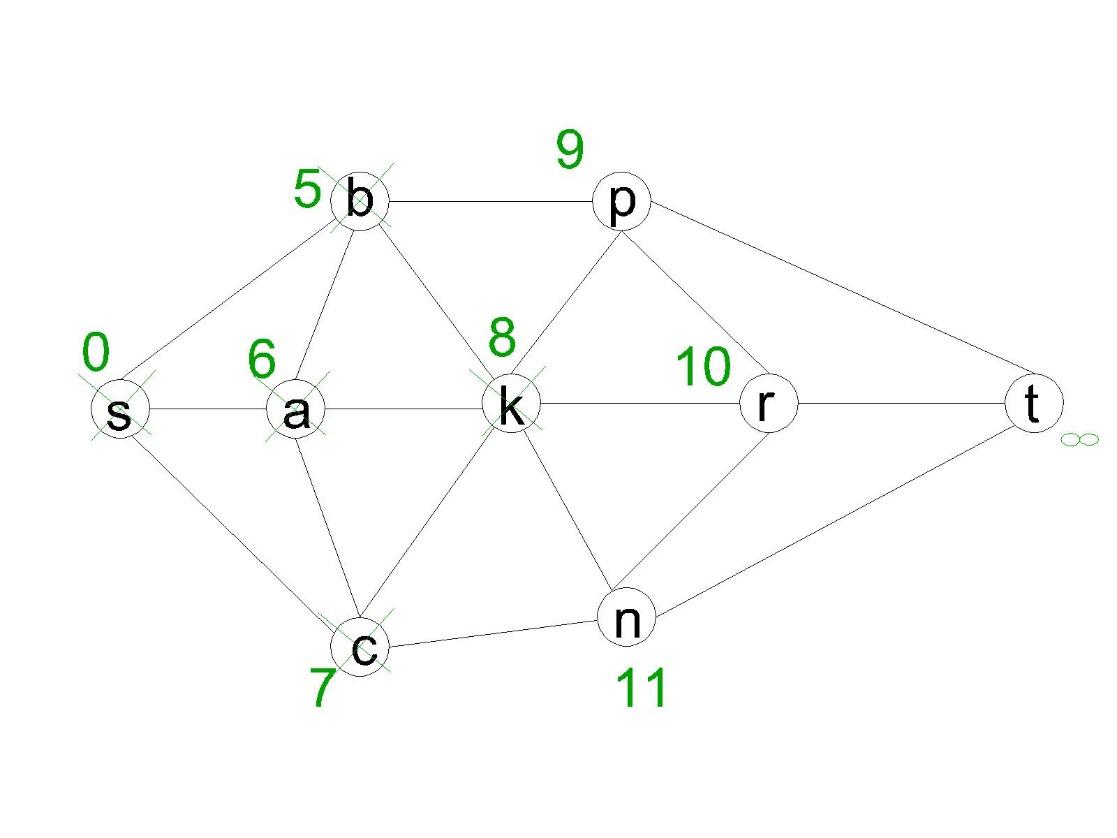
Ближайшая из непосещённых вершин –
вершина ![]() .
Из неё можно попасть в вершины
.
Из неё можно попасть в вершины ![]() и
и ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]()
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() останется равным
останется равным ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]() ).
).
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() станет равен
станет равен ![]() .
Вершина
.
Вершина ![]() становится посещённой, поэтому вычёркиваем
её. Получим:
становится посещённой, поэтому вычёркиваем
её. Получим:
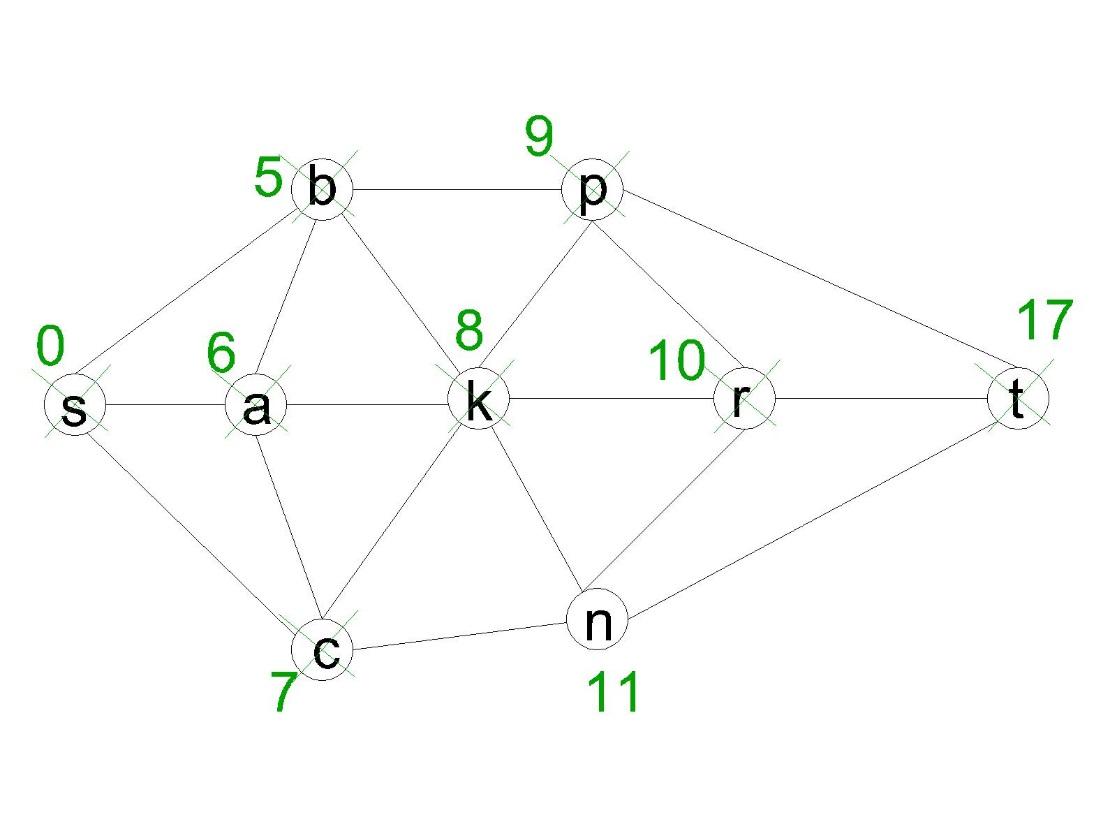
Ближайшая из непосещённых вершин –
вершина ![]() .
Из неё можно попасть в вершину
.
Из неё можно попасть в вершину ![]() .
Путь в вершину
.
Путь в вершину ![]() будет равен
будет равен ![]() .
.
![]() ,
поэтому вес вершины
,
поэтому вес вершины ![]() останется равным
останется равным ![]() .
Вершина
.
Вершина ![]() становится посещённой, поэтому вычёркиваем
её. Из вершины
становится посещённой, поэтому вычёркиваем
её. Из вершины ![]() больше никуда попасть нельзя, поэтому
её также вычёркиваем Получим:
больше никуда попасть нельзя, поэтому
её также вычёркиваем Получим:
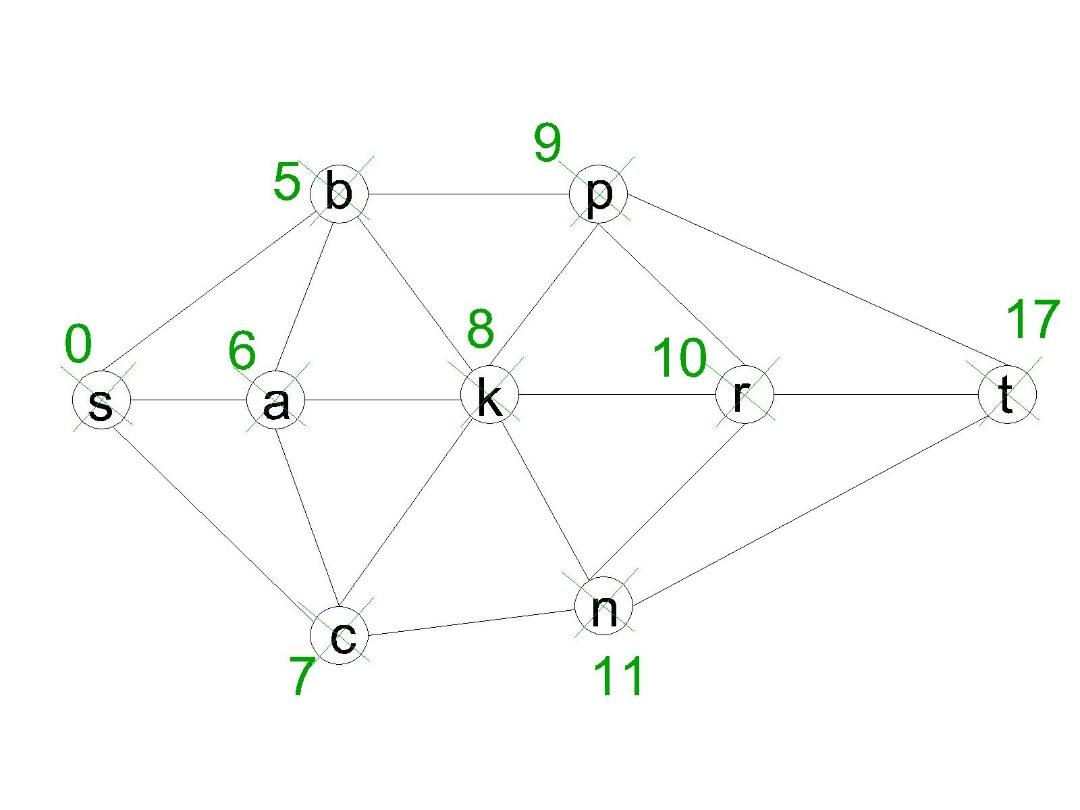
Все вершины графа получились вычеркнутыми.
Поэтому найдены минимальные пути из
вершины ![]() во все остальные. Вес вершины
во все остальные. Вес вершины ![]() равен
равен ![]() ,
поэтому кратчайший путь из вершины
,
поэтому кратчайший путь из вершины ![]() в вершину
в вершину ![]() равен
равен ![]() .
.
Пути следующие:
![]()
![]()
![]()
![]()
2. Найти максимальный поток в заданной транспортной сети, используя алгоритм Форда-Фалкерсона. Проверить ответ по теореме Форда-Фалкерсона (найти минимальный разрез графа сети).
Решение
С помощью алгоритма Форда-Фалкерсона
найдем наибольший поток из ![]() в
в ![]() .
.
Шаг 1. Выбираем произвольный поток,
например, ![]() .
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть
.
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть ![]() .
Уменьшаем пропускные способности дуг
этого потока на
.
Уменьшаем пропускные способности дуг
этого потока на ![]() ,
насыщенную дугу
,
насыщенную дугу ![]() вычеркиваем.
вычеркиваем.
Шаг 2. Выбираем произвольный поток,
например, ![]() .
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть
.
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть ![]() .
.
Уменьшаем пропускные способности дуг
этого потока на ![]() ,
насыщенную дугу
,
насыщенную дугу ![]() вычеркиваем.
вычеркиваем.
Шаг 3. Выбираем произвольный поток,
например, ![]() .
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть
.
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть ![]() .
.
Уменьшаем пропускные способности дуг
этого потока на ![]() ,
насыщенную дугу
,
насыщенную дугу ![]() вычеркиваем.
вычеркиваем.
Шаг 4. Выбираем произвольный поток,
например, ![]() .
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть
.
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть ![]() .
.
Уменьшаем пропускные способности дуг
этого потока на ![]() ,
насыщенную дугу
,
насыщенную дугу ![]() вычеркиваем.
вычеркиваем.
Шаг 5. Остался один возможный поток,
например, ![]() .
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть
.
Его пропускная способность равна
минимальной из всех пропускных
способностей входящих в него дуг, то
есть ![]() .
Уменьшаем пропускные способности дуг
этого потока на
.
Уменьшаем пропускные способности дуг
этого потока на ![]() ,
насыщенные дуги
,
насыщенные дуги ![]() вычеркиваем.
вычеркиваем.
Больше путей нет. Суммарный поток равен:
![]() .
.

Начинаем расстановку пометок. Начальная
вершина (источник) ![]() имеет пометку 0. Из этой вершины нет
ненасыщенных дуг, поэтому большепометки
расставить нельзя.
имеет пометку 0. Из этой вершины нет
ненасыщенных дуг, поэтому большепометки
расставить нельзя.
Значит, максимальный поток найден,
причем ![]() (непомеченные вершины) образуют разрез.
Источником теперь является вершина
(непомеченные вершины) образуют разрез.
Источником теперь является вершина
![]() .
Величина разреза
.
Величина разреза ![]() .
.
