6

Элементы линейной алгебры.

Одной из важнейших особенностей векторов является возможность производить над ними линейные операции – сложение и умножение на число.

Пусть R – множество всех векторов. Тогда, если

1. a Є R , b Є R, то и a + b Є R,

2. a ЄR, λ – действительное число, то λa ЄR.

Таким образом, сложение и умножение на число не выводит нас за пределы множества R.

Известно, что если задать три единичных взаимно перпендикулярных вектора i, j, k, то каждый трехмерный вектор представляется как упорядоченная тройка чисел – его координат. По аналогии дается определениеn–мерного вектора.

Упорядоченная система из n действительных чисел называется n – мерным вектором. Этот вектор записывается в виде x = {x₁, x₂, …, x_n }.

Рассмотрим множество n – мерныхвекторовR и, по аналогии с трехмерными векторами, введем операции сложения и умножения на скаляр.

Суммой двух векторов x = {x₁, x₂, …, x_n} и y= {y₁,y₂, …,y_n} называется вектор

z={z₁,z₂, …,z_n} (z = x + y), координаты которого равны суммам соответствующих координат слагаемых векторов, т.е.z_i = x_i + y_i .

Произведением вектора x на скаляр λ называется вектор λx,координаты которого представляют собой произведение числа λ на соответствующие координаты вектораx, т.е. λx= {λx₁, λx₂, …, λx_n}.

Множество R называется линейным пространством, а его элементы векторами, если

1. задан закон, по которому двум любым векторам x иy из R ставится в соответствие вектор x + y ЄR, называемый их суммой;

2. задан закон, по которому каждому элементу x Є R и числу λ ставится в соответствие вектор λx Є R, называемый произведением вектора x на число λ;

3. для любых векторов x, y, z из R и любых чисел α и β выполняются следующие аксиомы:

   1. x + y = y + x (коммутативность)

   2. (x + y) + z = x + (y + z) (ассоциативность);

   3. существует элемент 0 Є R, такой, что x + 0 = x для любого вектора x Є R;

0 = {0, 0, …, 0}

4. для каждого элемента x Є R существует элемент -x ЄR, такой, что x + (-x) = 0 (элемент -x называется противоположным элементом);

5. α(x + y) = αx + αy;

6. (α + β) x = αx + βx;

7. α(βx) = (αβ)x;

8. 1∙ x = x.

Примерами линейных пространств являются пространство обычных векторов (направленных отрезков), пространство n – мерных векторов, а также объекты другой природы (многочлены степени≤ n, комплексные числа и др.).

Линейно зависимые и линейно независимые векторы.

Система n векторов x_1, x₂ , …, x_n называется линейно зависимой, если существует такая система чисел α₁,α₂, …, α _n, не равных нулю одновременно, что

α₁ x₁ + α₂ x₂ + α_n x _n = 0. (*)

В противном случае векторы называются линейно независимыми.

Пусть векторы x₁ , x₂ , …, x_nлинейно зависимы. Тогда, по крайней мере, одно значение α не равно нулю. Пусть это α₁. Тогда

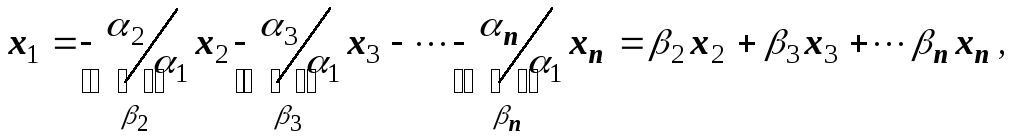т.е. векторx₁является линейной комбинацией векторовx_1, x₂ , …, x_n. Следовательно, если векторы линейно зависимы, то, по крайней мере один из них является линейной комбинацией остальных.

И обратно, если хотя бы один из векторов системы x_1, x₂ , …, x_n является линейной комбинацией остальных векторов, то система линейно зависима.

Пусть x₁=, тогда соотношение (*) примет вид

–x₁+=0, β ₁= -1.

Система линейно зависима.

П р и м е р ы .

1. Система x, x, y, z линейно зависима, т.к.x = 1∙x + 0∙y+ 0∙z.

2. Система 0, x, y, zлинейно зависима, т. к. 0 = 1∙0+ 1∙x + 1∙y + 1∙z.

3. Система трех некомпланарных векторов (направленных отрезков) линейно независима.

c

В противном случае c = α∙a + β∙b, т.е. с лежит в плоскости

b векторовa и b,что противоречит условию.

a

Однако, любые четыре вектора пространства линейно зависимы.

c d = OP₁ + P₁P + PD = α a + β b + γ c

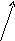D

d

O P₂ b

P₁ P

a

4. Система двух неколлинеарных векторов a и b плоскости линейно независима. В противном случаеb = αa, т.е. векторы коллинеарны. Однако любые три вектора плоскостилинейно зависимы.

P₂ c = OP₁ + OP₂ = α a + βb.

b c

a P₁

Линейное пространство называется n – мерным, если в нем существует система n линейно независимых векторов, но любые n + 1 векторов линейно зависимы.

Т.е. размерность пространства – это максимальное число линейно независимых векторов, содержащихся в нем.

Размерность множества всех обычных пространственных векторов равна трем.

Размерность множества всех плоских векторов равна двум.

Размерность множества всех коллинеарных векторов равна единице.

Т е о р е м а.

Если x₁, x₂ , …, x_n - система n линейно независимых векторов, принадлежащих пространству R, и каждый вектор x ЄRпредставляется как линейная комбинация векторов x₁, x₂ , …, x_n,то размерность пространства равна n.

Действительно, пространство содержит n линейно независимых векторов, а любые векторыx, x₁, x₂ , …, x_nлинейно зависимы.

О п р е д л е н и е . Упорядоченная система n линейно независимых векторов n-мерного пространства называется базисом.

Т е о р е м а.

Каждый вектор x линейного пространства представляется, и притом единственным образом, как линейная комбинация векторов базиса.

Пусть e₁, e₂ , … , e_n– базисn-мерногопространства,x – произвольный вектор этого пространства. Система векторовe₁, e₂ , … , e_n,x– линейно зависима, т.к. пространствоn-мерно. Следовательно, существует такая система чисел, не равных нулю одновременно, что

α₁ е₁ + α₂ e₂ + … + α _n e _n + α x=0.

α ≠ 0, т.к в противном случае, векторыe₁, e₂ , … , e_n были бы линейно зависимы. Отсюда

x =

Полагая -α_i /α = x_i ( i = 1, 2, …,n), получим

(*) x = x₁e₁ + x₂ e₂ + … + x_n e_n– линейная комбинация векторовe_i.

Это представление единственно, т.к., если вектор x можно представить через векторы базисаe_iв виде

x = y₁ e₁ + y ₂ e₂ + … + y _n e_n, то

(x₁ – y₁) e₁ + (x₂ – y₂) e ₂ + ... + (x_n – y_n)e _n = 0

В силу линейной независимости векторов базиса e_i, имеемx₁ =y₁, x₂ = y₂ , ... , x _n = y _n.

Числа x₁, x₂, ... , x _nназываются координатами векторах.

x = { x₁, x₂, ... , x _n}.

Таким образом, задание координат вектора в определенном базисе вполне определяет вектор.

П р и м е р . Рассмотрим множество обычных пространственных векторов (направленных отрезков). В качестве базиса можно взять векторы i, j, k.

a = X i+Yj+Zk− разложение вектора по векторам базиса.X,Y,Z– координаты вектораа.