
Konspekt_za_2y_semestr_po_fizike
.pdfКонспект лекций по физике за 2 семестр
По теме: Колебания и волны. Квантовая механика.
Преподаватель: Постников С. А.
Конспект подготовила: Багаутдинова Д. Ж. группа СС0606
Москва 2007г.
1
Содержание:
Часть3. Колебания и волны Глава 1. Колебания и волны
§1.1. Свободные гармонические колебания. Уравнение и начальные условия ………..1 §1.2.Затухающие колебания ………………………………………………………………..4
§1.3. Энергия свободных колебаний…………...……………………………………….....6
§1.4. Вынужденные колебания. Анализ решения. Резонансные характеристики...……7
§1.5. Вынужденные колебания. Переходный процесс...…………………………………11
§1.6. Сложение гармонических колебаний двух частот………………………………….14
§1.7. Физические основы анализа Фурье………………………………………………….16
Глава 2. Волны §2.1. Волновой процесс. Волновая функция……………………………………………….18
§2.2 Гармонические волны…………………………………………………………………21
§2.3. Распространение волны в ограниченной среде. Стоячие волны…………………...22 §2.4. Интерференция волн двух источников……………...………………………………..25 §2.5. Многолучевая интерференция…………………………...……………………………29
§2.6. Дифракция, принцип Гюйгенса……………………………………………………….31
§2.7. Дифракционная решетка……………………………………………………………….34
§2.8. Принцип Гюйгенса – Фринеля. Дифракция Фринеля……………………………….37
§2.9. Волновой пакет…………………………………………………………………………40
§2.10. Групповая скорость. Метод стационарных фаз……………………………………..43 §2.11. Пространственная и временная когерентность. Поляризация……………………..45 §2.12. Приближение геометрической оптики. Уравнение Эйконала. Принцип Ферма…48 §2.13. Электромагнитные волны в вакууме………………………………………………...50 §2.14. Энергия электромагнитного поля. Вектор Умова-Пойнтинга……………………..52 Часть 4. Квантовая механика
§1. Экспериментальные основы квантовой механики…………………………………….53
§2. Волны де Бройля…………………………………………………………………………56
§3. Уравнение Шредингера………………………………………………………………….57
§4. Принцип неопределенности Гейзенберга………………………………………………60
§5. Движение частицы в поле с потенциальным барьером. Туннельный эффект……….61
§6. Частица в потенциальной яме. Дискретность энергетических состояний…………...64
§7. Атом водорода……………………………………………………………………………66
§8. Принцип Паули. Периодическая таблица элементов………………………………….68
§9. Электрон в периодическом поле. Энергетические зоны……………………………....70
2
Часть 3
Колебания и волны
§1.1 «Свободные гармонические колебания. Уравнение и начальные условия.»
Для описания число независимых переменных необходимо для описания механических систем называется числом степеней свободы.
Рассмотрим систему с одной степенью свободы для описания которой будем использовать одну переменную х. Это могут быть либо координата, либо угол, либо заряд. В целом ряде задач эта переменная удовлетворяет уравнению вида
d 2 x |
2 x 0 |
|
|
dt 2 |
0 |
|
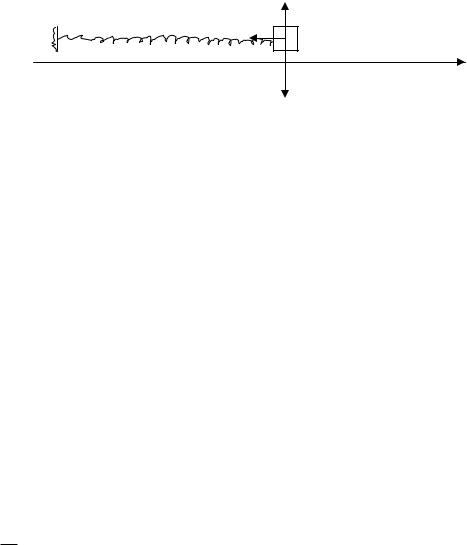
В качестве примера такой системы возьмём пружинный маятник без трения.
N
Fy
0
X
mg
max Fy |
ax-первая производная проекции скорости |
|||||||||||
Fy k l |
||||||||||||
|
|
|
||||||||||
l - изменение длинны |
|
|
|
|||||||||
a |
|
|
d 2 x |
|
|
|
|
|||||
x |
dt 2 |
|
|
|
||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
l x |
|
|
|
|
|
|
|
|||||
m |
d 2 x |
|
kx |
|
|
|
||||||
dt 2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
d 2 x |
|
k |
x 0 |
|
k |
2 |
||||||
|
|
|
|
|
|
|||||||
dt 2 |
|
m |
|
m |
0 |
|||||||
|
|
|
||||||||||
|
d 2 x |
2 x 0 |
-называется линейным, дифференциальным, однородным 2-го порядка. |
|
|
||
|
dt 2 |
0 |
|
|
|
|
|
Будем искать решение в виде |
|||
x A cos(t 0 )
Подставим функции в уравнение dxdt Asin(t 0 ) *
3
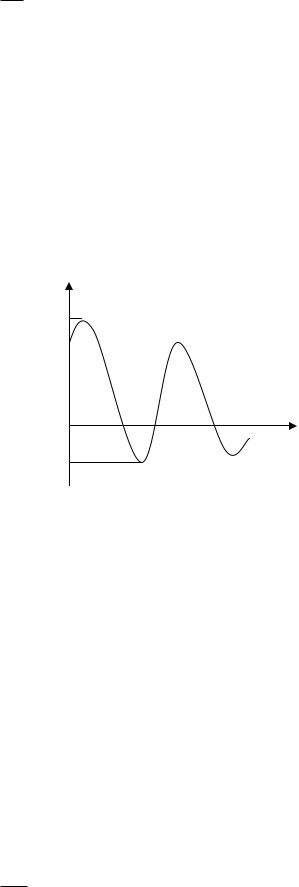
d 2t A cos(t 0 ) dt
A 2 cos( t 0 ) 0 2 Acos( t 0 ) 0
2 0 2 0
0
x Acos(0t 0 )
Полученное решение называется гармоническим колебанием, |
d 2 x |
2 x 0 |
, |
|
|||
|
dt 2 |
0 |
|
|
|
|
называется уравнение гармонических колебаний .
Система которая описывает уравнение называется гармоническим осциллятором.
x
А
t
-А
Амплитуда
колебаний
|
|
1 |
с 1 |
|
0 |
циклическая частота |
|
|
|
|
||||
|
|
с |
|
|
0t 0 -фаза колебаний
0 -начальная фаза
t- в течение которого фаза колебаний меняется на 2 ,период колебания
0 (t T ) 0 (0t 0 ) 2
0T 2
T |
2 |
|
c |
||
0 |
|
||||
|
|
|
|||
|
1 |
|
частота колебаний C 1 Гц |
||
T |
|||||
|
|
|
|||
0 2 x 0
d 2 x 0 dt 2
Поэтому значение x = 0 называют положением равновесия.
А величину x называют смещением независимо от того что она из себя представляет.
4
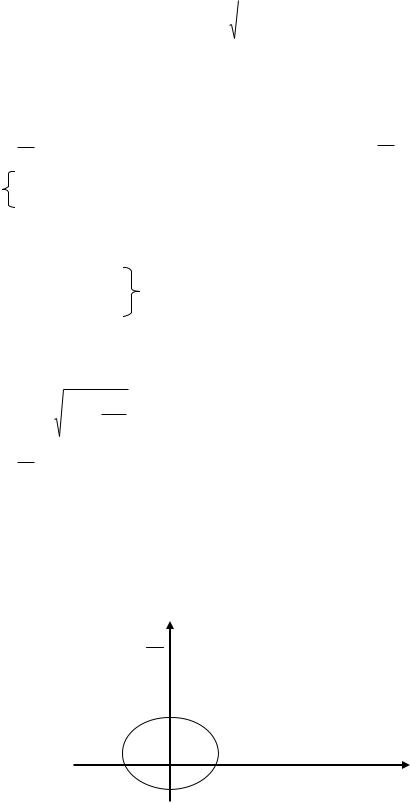
Полученное решение содержит 2 произвольные постоянные величины A,0 .
Уравнение гармонических |
колебаний определяет лишь частоту колебаний в |
||||
|
|
|
|
|
|
рассматриваемом примере. 0 |
|
k |
|||
|
|
||||
m |
|||||
|
|
|
|||
Для определения амплитуды и начальной фазы необходимо дополнительные условия, в качестве таких условий обычно используют начальные условия задачи , то есть значение смещения.
x Acos( 0t |
) |
dxdt A 0 sin( 0t 0 )
x0 |
A cos 0 |
|
|
|
|
||||||
V0 |
A 0 sin 0 |
|
|||||||||
tg 0 |
V0 |
|
0 |
|
|||||||
|
|
|
|
||||||||
|
|
|
|
|
o x0 |
|
|||||
x0 |
A cos 0 |
|
|
|
2 |
||||||
|
V0 |
Asin 0 |
+ |
||||||||
2 |
|||||||||||
|
|||||||||||
|
0 |
|
|
|
|
|
|
|
|||
A2 |
x |
2 |
|
V |
2 |
|
|
||||
|
0 |
|
|
||||||||
0 |
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
|
|
|
A x0 2 V0 20 2
dxdt - фазовая плоскость
y
dx
dt
A 0
x(0) x0 dxdt (0) V0
Гармоническое колебание фазовой плоскости будет иметь элипс
x
x Acos( |
t |
|
) |
dx |
A |
|
sin( |
t |
|
) |
0 |
|
0 |
0 |
|||||||
0 |
|
|
dt |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
x2 |
dx 2 |
1 |
|
||
|
|
|
|
|
1 |
A2 |
|
A2 2 |
|||
dt |
|
||||
|
|
|
|
0 |
|
5
|
|
|
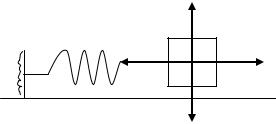
§1.2 |
Затухающие колебания. |
Рассмотрим систему в |
которой |
есть сила трения пропорциональная скорости. На |
||
|
|
|
|
|
которую действует |
F |
V |
|
|
|
r |
|
|
|
-коэффициент трения
N
Fy
FR
mg
FRx Vx |
|
|
|
|
|
|
||||||||||
ma x |
|
Fy Vx |
||||||||||||||
m |
d 2 x |
|
kx |
dx |
|
|
||||||||||
dt 2 |
dt |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
d 2 x |
|
|
|
dx |
|
k |
x 0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
dt 2 |
|
m dt |
m |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||
d 2 x |
2 |
dx |
|
|
2 x 0 |
|||||||||||
|
|
0 |
||||||||||||||
dx2 |
|
|
|
|
|
dt |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
k |
|
|
|
|
|
2 |
|
|||||
0 |
|
m |
|
|
|
|
m |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Для того чтобы найти решение уравнения затухающих колебаний рассмотрим уравнение в котором х комплексная величина.
dx2 |
2 |
dx |
0 2 x 0 |
|
dt 2 |
dt |
|||
|
|
Реальная часть которых = 0
d 2 x |
2 |
dx |
|
2 x 0 |
|
|
|||
dt 2 |
|
dt |
0 |
|
|
|
|||
Очевидно, что реальная часть комплексного уравнения является уравнение затухающих колебаний поэтому реальная часть решения комплексного уравнения будет решением уравнения затухающих колебаний.
Re x x
Будем использовать решение уравнения
x Ae i(n )
6
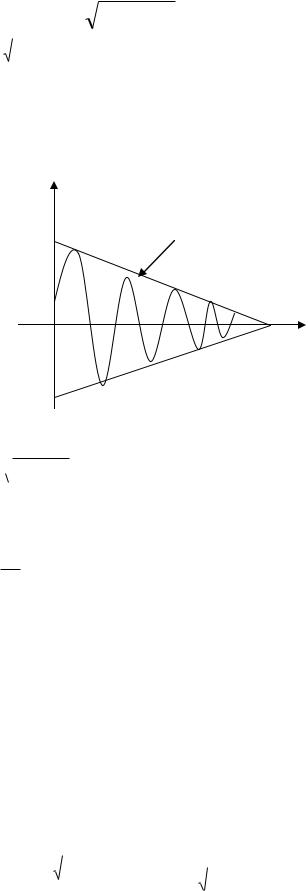
2 Aei( t ) i2 Aei( At ) 02 Aei( t ) 0
2 i2 0 2 0
|
1,2 |
i 2 2 i |
|
|
|||
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
||
|
|
|
0 |
|
|
|
|
x Aei ( t 0 ) |
Ae t e i ( t 0 ) |
|
|
||||
x Re x Ae t Re i ( t 0 ) Ae t cos(t |
0 |
) |
|||||
|
|
|
|
|
|
|
|
x
Ae t
t
Ae t - амплитуда затухающих колебаний.

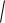 0 2 2 -частота затухающих колебанийt 0 -фаза колебаний
0 2 2 -частота затухающих колебанийt 0 -фаза колебаний
T- в течение которого фаза колебаний меняется на 2 , называется периодом затухающих колебаний.
T 2
Время в течение которого амплитуда колебаний уменьшается в Е раз, называется временем релаксации
|
1 |
|
|
|
|
||
|
|
||||||
|
|
|
|||||
|
d 2 x |
2 |
dx |
|
2 x 0 |
||
|
|
|
|||||
|
dt 2 |
|
|
|
dt |
0 |
|
|
|
|
|
|
|||
aib c id
x Aei( t )
2 Aei( t ) i 2Aei(2t ) 0 2 x 0
2 2i t 0 2 0
2 2i 2 |
0 |
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2i |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
i 2 |
|
|||||
|
|
|
|
|
|
0 |
|
|
2 |
||
1,2 |
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
7

x Aei ( t ) |
Aei ( )t |
Ae t e i ( t ) |
|
|
|
|
||||||||||
x |
2 |
Re x Ae t |
cos(t ) |
|
|
|
|
|
|
|||||||
|
ln |
|
|
Ae t |
|
T |
|
|
|
|
|
|
||||
|
|
Ae j (t T ) |
|
|
|
|
|
|
||||||||
- декремент затухания |
|
|
|
|
|
|
||||||||||
Заметим, |
|
что |
полученное |
решение |
будут |
справедливо |
если |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
2 действительная величина, |
а это возможно если |
|
0 |
. В этом случае |
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
говорят, что система находиться в «периодическом режиме», решим, если 0 , то |
|
|||||||||||||||
|
|
|
|
|
|
|
||||||||||
i |
|
2 2 |
i i , где -действительная величина, тогда |
|
|
|
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
i( ) |
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
(всегда) |
|
|
|
|
|
|
|
|
||||||
x Ae( t ) |
Ae(t )t ei |
|
|
|
|
|
|
|||||||||
xRe x Ae ( )t cos
Вэтом случае никаких колебаний в системе не происходит она просто стремиться к положению равновесия, в зависимости от того какие были начальные условия. В этом случае происходит апериодический режим.
Если 0 . То режим называется критическим.-коэффициент затухания (декремент затухания)
§ 1.3 Энергия свободных колебаний
Колебания рассмотренные в §1.2 принято называть свободными так как они происходят в системе без воздействия внешних сил. Внешние влияние происходит лишь
вначальный момент времени, когда система выходит из положения равновесия. Рассмотрим полную энергию гармонических колебаний, на примере пружинного
маятника координаты которого меняться по закону x A0 cos(0t ) , полная энергия
T |
mV 2 |
, где T- кинетическая энергия |
|
||
2 |
|
|
V k2x2 -потенциальная энергия пружины
V k2 A0 cos2 (0t )
V dxdt 0 A0 sin(0t )
V 2 V |
2 |
|
|
2 A 2 sin2 ( t ) |
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
E |
k |
A |
2 cos2 ( |
|
t ) |
m |
2 |
A 2 |
sin 2 ( |
2t ) |
|
||||||||
|
0 |
|
|
||||||||||||||||
|
2 |
|
0 |
|
|
|
2 |
0 |
|
0 |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E |
kA |
2 |
|
(cos 2 ( |
t ) sin 2 ( |
t )) |
|
kA |
2 |
E |
|
||||||||
0 |
|
|
|
0 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
0 |
|||||||||||
|
2 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E - постоянна и пропорциональна квадрату амплитуды.
Рассмотрим полную энергию затухающих колебаний пружинного маятника. x A0 e t cos(t ) , при этом затухание слабое
0

 0 2 2 0
0 2 2 0
8
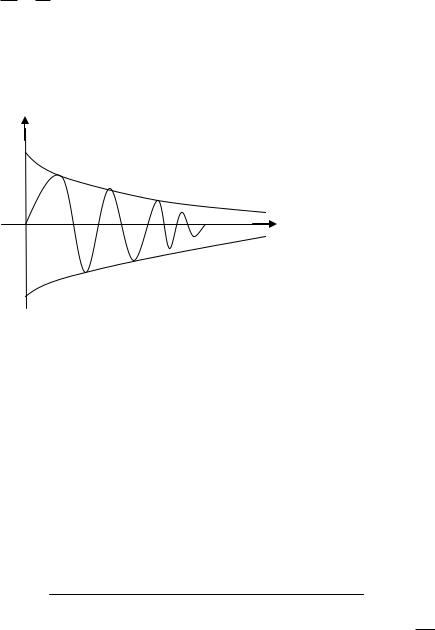
Vx dxdt dtd A0 e t cos(t )
Так как затухание слабое то можно считать, что первый сомножитель амплитуды A0 e t практически не меняется за время в течение которого второй сомножитель (cos(t )) меняется очень сильно, то есть за время одного периода колебаний.
При вычислении производной можно считать A0 e t константой.
V |
|
A |
t |
d |
cos(t ) A e t sin(t ) |
|
|
|
|||||||||||||||
x |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
0 |
|
|
dt |
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E |
kx2 |
|
|
mv 2 |
|
k |
A 2 e 2 t cos2 (t ) |
m |
|
2 A |
2 e 2 t sin 2 |
(t ) |
|||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
2 |
2 |
0 |
2 |
|
|
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
k |
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
m |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
E |
k |
A |
2 e 2 t (cos2 (t ) sin |
2 (t )) |
k |
A |
2 e 2 t E |
e 2 t |
|||||||||||||||
|
|
||||||||||||||||||||||
|
|
2 |
|
0 |
|
|
|
|
|
|
|
2 |
0 |
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Энергия затухающих колебаний будет уменьшаться со временем точно также как квадрат амплитуды.
Добротностью осциллятора называется
Q 2
Энергия запасённая осциллятором
Энергия теряемая за период
Энергия которую теряет осциллятор за единицу времени будет dEdt 2E0 e 2 t тогда за период осциллятор потеряет энергию 2E0 e 2tT тогда
|
E |
e 2 t |
|
|
Q 2 |
0 |
|
|
t |
2 E |
|
e 2 tT |
||
|
0 |
|
|
|
Зная добротность можно оценить сколько колебаний совершит система выведенная из положения равновесия
Q 1 10
Просто струна 103 (добротность) Добротность атома – 1012 – самая высокая
§1.4 Вынужденные колебания Анализ решения. Резонансные характеристики.
Рассмотрим систему на которую действует внешняя сила F . Если это пружина маятника, то уравнение будет иметь вид:
9
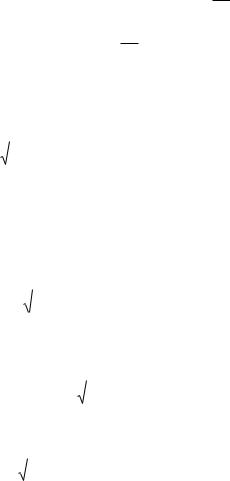
m |
d 2 x |
|
kx |
dx |
F |
|||||||
|
|
|||||||||||
|
dt 2 |
|
|
|
|
|
|
|
dt |
x |
||
|
|
|
|
|
|
|
|
|
||||
d 2 x |
|
|
dx |
|
k |
x F |
|
|||||
|
|
|
|
|
|
|
|
|||||
dt 2 |
|
|
m dt |
|
m |
|
|
x |
|
|||
|
|
|
|
|
|
|
||||||
Рассмотрим самый важный случай когда внешняя сила периодична.
Fx F0 cost
d 2 |
2 |
dx |
|
|
2 |
x |
F |
cos(t) |
|
|
|
|
0 |
||||
dt 2 |
dt |
0 |
|
m |
||||
|
|
|
|
|
||||
|
|
|
|
|
|
Для того чтобы найти решение этого уравнения рассмотрим комплексное уравнение реальная часть которого совпадает с нашим уравнением.
d 2 x |
|
dx |
|
|
2 |
|
|
F |
|
|
2 |
|
|
|
|
x 2 |
|
0 |
ei t |
dt 2 |
|
0 |
|
|
|||||
|
dt |
|
|
|
|
m |
|||
|
|
|
|
|
|
||||
Решение уравнения будем искать в виде: x x0 ei t
2 x0 ei t i2x0 ei t 0 2 x0 ei t Fm0 ei t
x0 (0 2 2 i2 ) F0 m
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
F0 |
|
|
|
|
|
|||||||
|
m |
2 |
2 i2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
R ( |
2 |
2 )2 4 2 2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
tg( ) |
|
|
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
0 |
2 |
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg() |
|
|
|
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X 0 |
|
|
|
|
|
|
|
|
|
|
F ei |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m ( |
2 2 )2 4 2 2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
|
ei t |
|
|
|
|
|
|
F ei( t ) |
|
|||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
m ( 2 2 )2 |
2 2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
x Re x x0 |
cos(t ) , где |
|
|
|
|
||||||||||||||||||||
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
F0 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
m 2 |
2 )2 4 2 2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом найденное решение уравнения вынужденных колебаний представляет собой гармонические колебания амплитуда которых полностью определяется параметрами осциллятора и частотой -вынуждающая сила
Тоже самое касается и начальной фазы колебаний . Другими словами полученное
решение независит от начальных условий, а поэтому не является общим и единственным. Это частное решение уравнения вынужденных колебаний.
10
