
Dushevnye_otvety_na_test_po_fizike
.pdf
(!) 1. Каноническое распределение Гиббса имеет вид Pi = Ce− kTεi , где постоянная С
|
|
C = |
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
равна: |
*С) |
∑e− |
εi |
; |
|
|
|||||||
|
|
|
|
||||||||||
kT |
|
|
|||||||||||
|
|
|
|
|
i |
|
|
||||||
|
|
|
|
|
− |
( εi −µN ) |
|
|
|
||||
|
|
|
e |
kT |
|
|
|||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
(!) 2. Выражение |
|
|
|
|
− |
( εi −µN ) |
: |
||||||
∑∑e kT
Ni
*С) равно вероятности встретить подсистему, состоящую из N частиц, в состоянии с энергией εi;
(!) 3. |
υ |
|
можно найти, вычислив значение интеграла |
||||
|
|
2 |
|
|
|
|
|
∞ |
|
m |
3 |
2 |
|
|
|
|
|
|
2 |
−mυ |
|
|
|
|
|
|
4π...e 2kT dυ |
4 |
) |
||
|
|
|
|
|
|||
|
|
|
|
. (*Вставить υ |
|||
∫ |
2 kT |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
π |
|
|
|
|
||
0 |
|
|
|
|
|
|
|
(!) 4. Если F(x) – плотность вероятности или функция распределения случайной
+∞
величины х, то выражение ∫ f ( x) F ( x) dx = ....
−∞
(*Ответ: f ( x) ) или
Если F(x) – функция распределения случайной величины х, а f(x2) – некоторая
функция этой величины, то +∞∫ f (x2 )F (x)dx =
−∞
*C)  f (x 2 )
f (x 2 )
(!) 5. Если F(x) – плотность вероятности или функция распределения случайной
|
|
|
+∞ |
|
|
|
|
∫ x2 F ( x) dx |
+∞ |
величины х, то выражение |
−∞ |
= .... ; (*Ответы: x2 и ∫x2 F (x)dx и |
||
+∞ |
||||
|
|
|
∫ F ( x) dx |
−∞ |
|
|
|
|
|
|
|
|
−∞ |
|
|
x2 |
|
|
|
|
+∞ |
) |
|
|
|
∫F (x)dx |
|
|
|
−∞
(!) 6. F(x) – плотность вероятности или функция распределения случайной величины х. Среднее значение х 2 на интервале от х1 до х2 равно:
x2
|
∫ x2 F(x)dx |
|
*B) |
x1 |
; |
x |
||
|
2 |
|
|
∫ F(x)dx |
|
|
x1 |
|
(!) 7. Если F(x) – плотность вероятности или функция распределения случайной величины х, то  х3
х3  равно:
равно:

+∞
∫ x3F ( x) dx
*D) −∞+∞
∫ F ( x) dx
−∞
(!) 8. Средние скорости молекул идеальных газов, у которых Т1 = Т 2 , а массы молекул m1 > m2 :
*А) υ < υ ;
1 2
(!) 9. Если число молекул идеального газа выросло в четыре раза (N2=4N1), а Т1 = Т 2 и р1 = р2 , то относительное число молекул, имеющих скорости от υ до υ + dυ :
*С) осталось прежним;
(!) 10. f(p) - функция распределения по модулю импульса для молекул идеального
p 2
газа. Среднее значение m равно:
2
*В) 3kT ; 2
11. Критерием перехода квантовой статистики в классическую принято значение μ равное …(*Ответ: 0)
(!) 12. Молекулы идеального газа:
*С) могут иметь как целый, так и полу целый спин;
(!)13. При одинаковых температурах наиболее вероятная скорость молекул кислорода … наиболее вероятной скорости молекул водорода. (*Вставить: меньше)
(!)14. При одинаковых температурах средняя квадратичная скорость молекул кислорода … средней квадратичной скорости молекул водорода. (*Вставить: меньше)
(!)15. При одинаковых температурах средняя энергия молекул кислорода … средней энергии молекул водорода. (*Вставить: равна)
(!)16. Наиболее вероятное значение энергии для молекул идеального газа:
*D) не зависит от m.
(!) 17. Для функции распределения Максвелла по проекции импульса
0
∫ f ( p x )dp x =.... (*Ответ: 0,5 – запятая.)
−∞
(!) 18. Для функций распределения Максвелла по проекциям импульсов
00
∫ ∫ f ( p x ) f (p y )dp x dp y =.... (*Ответ: 0,25 – запятая.)
−∞−∞
19. Среднее значение 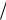 mυ2
mυ2 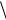 для идеального газа можно рассчитать, пользуясь
для идеального газа можно рассчитать, пользуясь
2
любым выражением, кроме …

|
|
∞ |
|
|
3 |
|
|
|
|
mυ2 |
|
|
|
m |
|
m 2 |
|
|
|
_ |
|
||||
*А) |
∫ |
4πυ |
2 |
e |
2κΤ dυ ; |
|||||||
|
|
|
|
|
|
|||||||
|
2 |
0 |
2πκΤ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
20. Максимальное значение плотности вероятности f ( px ) с увеличением массы молекул (при Т=const) … (*Вставить: уменьшается)
(!) 21. В функции распределения Максвелла по проекции скорости
|
|
|
1 |
|
2 |
|
|
|
|
|
−mυx |
|
|
|
m |
2 |
|
m – это: |
||
f (υx ) = |
|
|
|
e |
2kT |
|
|
|
|||||
|
2πkT |
|
|
|
|
|
*А) масса одной молекулы определенного газа;
(!) 22. Плотность вероятности или функция распределения молекул идеального газа
|
|
|
|
|
|
_ mυx2 |
С |
|||
|
|
|
|
|
|
|
|
|
||
по проекции скорости имеет вид |
ϕ (υх ) = Се 2κΤ , где нормированный множитель |
|||||||||
|
||||||||||
равен: |
|
|
|
|
|
|
|
|
|
|
|
С = |
|
|
1 |
|
|
|
|
|
|
*C) |
+∞ |
е− |
mυx2 |
|
|
|
|
|||
|
|
|
|
|
||||||
|
∫ |
2kT dυ ; |
|
|
|
|
||||
|
|
|
x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
−∞
υ2
(!) 23. Значения интеграла ∫ f (υ ) dυ для разных газов( m1 ≠ m2 ) при одинаковых
υ1
температурах:
*D) нельзя сравнить, так как значения интеграла зависят от выбранного интервала скоростей.
(!) 24. Функция распределения молекул идеального газа по модулю скорости f (υ) (плотность вероятности) имеет размерность:
с *В) м ;
(!) 25. Правильным соотношением для функции распределения молекул идеального
|
|
|
|
|
|
|
|
|
|
|
1 |
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( px ) = |
1 |
2 |
− |
x |
|
||
газа по проекции импульса |
2mkT |
является: |
|||||||||||||
|
|
|
|
|
|
|
|
|
2πmkT |
|
e |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∞ |
|
|
1 |
|
px2 |
|
|
|
|
|
|
|
|
|
|
|
1 2 |
− |
|
|
|
|
|
|
|
|
|
||||
*А) ∫ |
2mκΤ dpx = 1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
e |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
−∞ |
|
2π mκΤ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(!) 26. На рисунке показано распределение Максвелла по модулю скорости для некоторого газа при разных температурах. При этом площади под кривыми (Si) и температуры (Тi) удовлетворяют соотношению:
f(υ)
1
2
3
υ

*А) S1=S2=S3=1, T3>T2>T1;
(!) 27. Вероятность встретить молекулы идеального газа, у которых проекции
скорости υч |
≥ 0 , υy ≥ 0 , а υz принимает любые значения, равна… |
|||||||
(*Ответ: 0,25) – запятая. |
||||||||
|
|
|
|
|
− |
ε |
|
|
|
|
2π ε |
|
|||||
|
|
|
|
|||||
(!) 28. |
f (ε ) = |
|
|
|
e κΤ |
- плотность вероятности или функция распределения молекул |
||
3 |
||||||||
|
|
|
||||||
(πκΤ) 2
по энергии. Среднее значение  ε
ε  молекулы идеального газа равно:
молекулы идеального газа равно:
∞ |
|
3 |
|
|
ε |
|
||
|
ε |
2 |
|
− |
|
|||
|
|
κΤ dε ; |
||||||
*В) ε = ∫ |
2π |
|
|
e |
|
|||
|
||||||||
0 |
|
πκΤ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(!) 29. Среднее значение  υ2
υ2  для молекул идеального газа равно любому
для молекул идеального газа равно любому
выражению, кроме:
*D)  υx
υx  2 +
2 +  υy
υy  2 +
2 +  υz
υz  2
2
(!) 30. f (x) = Ce−α x2 - плотность вероятности или функция распределения случайной
величины х, Нормированный множитель С равен:
1
*D) |
∞ |
−α x2 |
|
; |
|
∫ e |
|
dx |
|
|
−∞ |
|
|
|
(!) 31. Если ϕ (υx ) и ϕ (υy ) - плотности вероятности или функции распределения по
∞ ∞
проекциям скорости, то выражение ∫ ∫ υxυyϕ (υx )ϕ (υy ) dυx dυy =
−∞ −∞
*В) 0
(!) 32. Отношение наиболее вероятных значений энергий ε2н для двух газов, у
ε1н
которых m2=4m1, a Т2=Т1, численно равно…(*Ответ: 1)
(!) 33. Распределение Максвелла-Больцмана для идеального газа имеет вид:
dN |
1 |
|
|
|
ε |
|
|||
|
= |
|
|
|
exp − |
|
dxdydzdpx dpy dpz |
, где ε - |
|
|
|
3 |
|
|
|||||
N |
|
|
κΤ |
||||||
V ( 2π mκΤ) 2 |
|||||||||
|
|
|
|
|
|
|
|||
*В) потенциальная энергия частиц во внешнем поле плюс суммарная кинетическая энергия молекул
|
|
|
3 |
|
|
|
|
|
2 |
|
1 |
|
2 |
||||
|
|
|
|
|
|
|
− |
mυ |
|
|
|
|
− |
mυx |
|||
|
|
m 2 |
|
2 |
|
|
m 2 |
||||||||||
|
|
|
|
|
|
|
|||||||||||
(!) 34. Для функций распределения |
f (υ ) = |
|
|
4πυ |
|
e |
|
2kT |
и ϕ (υx ) = |
|
|
e |
2kT |
||||
|
|
|
|||||||||||||||
|
|
|
2π kT |
|
|
|
|
|
|
|
2π kT |
|
|
||||
справедливо соотношение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*В) ∫ f (υ)dυ = ∫ ϕ(υx )dυx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0−∞

35. ϕ (υx ) , ϕ (υy ) , ϕ (υz ) - плотности вероятности или функции распределения молекул
по проекциям скорости, для которых справедливо любое соотношение, кроме…
∞ |
1 |
∞ ∞ ∞ |
|
*С) ∫ ϕ (υx ) dυx = |
∫ ∫ ∫ ϕ (υx )ϕ (υy )ϕ (υz ) dυxdυy dυz ; |
||
3 |
|||
−∞ |
−∞ −∞ −∞ |
||
|
(!) 36. ϕ(υх ) - плотность вероятности или функция распределения по проекции
скорости для молекул идеального газа принимает значения:
|
|
1 |
|
*С) |
m 2 |
; |
|
x2πκΤ
37.Если функция распределения по энергии для идеального газа пронормирована(υ ) ≤< ϕ0
∞ |
ε2 |
на число частиц ( ∫F(ε )dε = N ), то интеграл ∫ε F(ε )dε равен:
0 ε1
*D) суммарной энергии всех частиц, у которых ε1 ≤ ε ≤ ε2
(!) 38. Наиболее вероятное значение проекции скорости υx для молекул идеального
газа равно:
*C) 0;
(!) 39. Отношение средних значений |
υ1 |
для двух разных газов, у которых Т1=3Т2, а |
υ2 |
m2=3m1, равно…(*Ответ: 3)
(!) 40. 3κΤ - это *D) средняя квадратичная скорость, где m – масса одной молекулы. m
(!) 41. Если отношение наиболее вероятных значений скоростей υ2нв = 2 , то
υ1нв
отношение максимальных значений f2max (υ ) = ... (*Ответ: 0.5) – запятая.
f1max (υ)
(!) 42. Распределение Максвелла по модулю скорости для некоторого идеального газа при Т1>Т2 показано на рисунке:
*В)
f(υ) |
2 |
|
1
υ
(!) 43. Функции распределения по проекции импульса рх (плотность вероятности) для разных газов, у которых m2>m1, а T1 = T2 , показаны на рисунке:
*В)
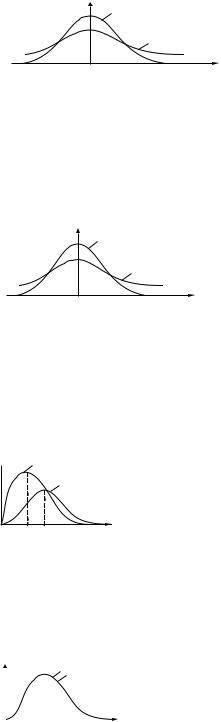
f(рх)
m1
m2
рх
(!) 44. Функции распределения молекул идеального газа по проекции скорости
(плотность вероятности) ϕ (υx ) для разных газов, у которых m2>m1, a T1=T2, показаны на рисунке:
* В)
φ(υх)
m2
m1
υх
(!) 45. Функции распределения по энергии f (ε ) для некоторого газа при Т2>Т1
показаны на рисунке:
*С)
 f(ε) Т1
f(ε) Т1
Т2
ε
46. Правильным рисунком плотности вероятности f(v) для одинаковых газов, у которых T2 = T1 , давление не меняется, а N2 > N1 , является:
*С)
f(υ) |
2 |
|
|
|
1 |
|
|
|
(графики совпадают |
) |
|
|
|
|
|
|
υ |
|
|
(!) 47. Если f (x) = ce−α x2 - плотность вероятности или функция распределения
случайной величины х ( х изменяется от -∞ до +∞), то справедливо любое выражение, кроме:
∞
*D) ∫се −αх2dx =c
−∞
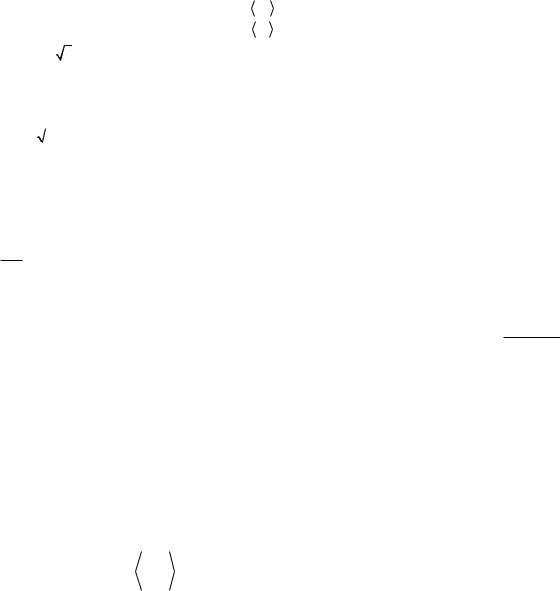
(!) 48. Если f (ε ) - плотность вероятности или функция распределения молекул идеального газа по энергии, то среднее значение  ε
ε  на интервале энергий от ε1 до ε2 равно:
на интервале энергий от ε1 до ε2 равно:
ε2
∫εf (ε)dε
*D) |
ε = |
ε1 |
; |
|
ε2 |
||||
|
|
|
∫ f (ε)dε
ε1
(!) 49. Если температура 2-х идеальных газов Т2=2Т1, а массы молекул m2=2m1, то
отношение значений средних энергий |
ε2 |
= ... (*Ответ: 2) |
|||||||||||||||||||||||||
ε1 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
50. |
f (ε ) = |
|
|
|
|
|
|
|
|
|
|
e κΤ |
- функция распределения молекул идеального газа по энергии, |
||||||||||||||
|
|
|
|
3 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
(πκΤ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
которая удовлетворяет любому соотношению, кроме: |
|||||||||||||||||||||||||||
|
∞ |
|
|
|
|
|
|
|
|
|
ε |
|
|
∞ |
|
|
|
3 |
|
|
mυx2 |
|
|
|
|||
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
2 2 |
− |
|
|
|
|||||||||
|
2π ε |
|
|
|
|
m |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
*D) ∫ |
|
|
e |
κΤ dε = ∫ |
|
|
|
υ |
e 2κΤ dυ . |
|
|
||||||||||||||||
3 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πκΤ |
|
|
|
|
|
|
|
||
|
0 (πκΤ) 2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(!) 51. Согласно теореме о равнораспределении энергии по степеням свободы
 υx2
υx2  +
+  υy2
υy2  равно:
равно:
*B) 2κΤ m
(!) 52. При увеличении температуры идеального газа Т2=4Т1 отношение
максимальных значений функций распределения по проекции скорости ϕ2max (υx ) = ...
ϕ1max (υx )
(*Ответ: 0,5 – запятая.)
(!) 53. f (υ) - плотность вероятности или функция распределения молекул
идеального газа по модулю скорости, для которой справедливо любое соотношение, кроме:
∞ |
∞ |
|
|
3 |
|
mυ2 |
|
||
|
m 2 |
− |
|||||||
*А) ∫ |
f (υ ) dυ = ∫ |
2κΤ dυ ; |
|||||||
|
|
|
e |
||||||
|
|||||||||
0 |
0 |
|
2πκΤ |
|
|
|
|||
|
|
|
|
|
|
|
|||
(!) 54. Средняя кинетическая энергия одного атома идеального газа равна 6,9·10-21
Дж. Среднее значение |
mυx2 |
= ... (*Ответ: 2,3·10-21Дж) Формат ответа: 2,3; -21 |
|
2 |
|||
|
|
(!) 55. Если х - случайная физическая величина, принимающая ряд дискретных значений х1, х2, …хп, а pi – вероятность появления xi, то среднее значение  х
х  равно:
равно:
n
*А)  x
x = ∑xi pi ;
= ∑xi pi ;
i=1
(!) 56. Выражение
∞ |
|
|
|
1 |
|
|
mυx2 |
|
|
m |
2 |
|
− |
|
|||
∫ |
|
|
|
υxe |
|
2κΤ dυx равно: |
||
|
||||||||
−∞ |
|
2πκΤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*D) 0.
(!) 57. Условием нормировки функции распределения Максвелла по модулю скорости для молекул идеального газа является выражение:
∞ |
|
|
3 |
|
|
|
|
|
mυx2 |
|
|
|
|
|
|
|
|
m 2 |
|
|
|
− |
|
|
|
|
|
|
|
||||||
*С) ∫ |
4πυ |
2 |
|
2κΤ dυ = 1 ; |
|
|
|
|
|||||||||
|
|
|
|
e |
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||
0 |
|
2πκΤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
m |
32 |
− |
mυ 2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
(!) 58. Интеграл ∫ |
|
|
|
|
|
|
4π |
3eυ 2k Tdυ = υ |
k , где k=…. (*Ответ: 1) |
||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
0 |
|
2πk T |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(!) 59. Графики 1,2,3 соответствуют трем функциям распределения Максвелла по модулю импульса для одного и того же газа в сосуде V при разных T. Наименьшей энтропии соответствует график ….. (*Ответ: 1)
f(р)
1
2
3
р
(!) 60. Среднее значение υx2 можно найти, пользуясь любым выражением, кроме…
|
|
∞ |
|
|
|
1 |
|
|
|
mυx2 |
|
|
|
|
m |
2 |
|
|
− |
|
|||
*С) |
2 |
|
2 |
|
2κΤ dυ x ; |
||||||
υx |
= ∫ |
|
|
|
|
υx |
e |
|
|||
|
|
||||||||||
|
|
0 |
2πκΤ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(!) 61. Если число молекул идеального газа увеличилось N2 = 2N1 , а T2 = T1 , p2 = p1 , V2 = 2V1 , то отношение вероятностей встретить молекулы с энергиями отε до ε + dε ,
dP2 =… (*Ответ: 1) dP1
(!) 62. Функция распределения молекул идеального газа по проекции скорости υх ,
пронормированная на 1, имеет вид:
|
|
|
1 |
|
mυx2 |
|
|
*В) |
m |
|
2 |
− |
; |
||
2κΤ |
|||||||
|
|
e |
|||||
|
|
|
|
|
|
|
|
|
2πκΤ |
|
|
|
|
||
(!)63. Для f (υ ) , плотности вероятности или функции распределения Максвелла по
модулю скорости, справедливо выражение:
*А) 0 < f (υ ) dυ < 1;
(!)64. Функция распределения Максвелла по модулю скорости (плотность вероятности) f(υ) равна:
*С) относительному числу молекул в единичном интервале скоростей;

 f(ε)
f(ε)
ε
ε1 ε1+dε
(!) 64,5. f (ε) - плотность вероятности
или функция распределения молекул идеального газа по энергии. Заштрихованная площадь равна:
*D) относительному числу молекул dN / N , имеющих энергию от ε1 до
ε1 + dε ;
(!)65. Основной постулат статической физики утверждает, что микросостояния, принадлежащие одной … , равновероятны. (Ответ: энергии)
(!)66. ϕ (υx ) , ϕ (υy ) , ϕ (υz ) - плотности вероятности или функции распределения
молекул идеального газа по проекциям скорости. Выражение
∞ ∞ ∞
∫∫∫ϕ (υx )ϕ (υy )ϕ (υz ) dυx dυy dυz = ... (*Ответ: 0,125 – запятая.)
0 0 0
67. Если f (υx ), f (υy ), f (υz ) - функции распределения по проекциям скоростей для
молекул идеального газа, то:
*D) |
|
m |
|
f (υx ,υy ) = |
|
e |
|
|
|||
|
|
2πkT |
|
|
m |
|
2 |
2 |
|
− |
|
υx |
+υy |
|
|
|
|||||
|
2kT |
|
|
|
|
68. Перейти от классической функции распределения по модулю импульса
|
4πυ |
2 |
|
|
|
|
|
p |
2 |
|
|
f ( p) = |
|
|
|
exp |
|
− |
|
|
к функции распределения по модулю скорости f(υ): |
||
|
3 |
|
|
2mkT |
|
||||||
|
|
|
|
|
|
|
|
|
|
||
|
(2πmkT ) 2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
*B) можно, заменив p на mυ и dp на mdυ в выражении f(p)dp;
или
Перейти от классической функции распределения по модулю скорости
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
m 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
mυ |
|
|
к функции распределения по энергии f(ε) |
||||||||||
f (υ) = |
|
|
4πυ |
|
exp |
− |
|
|
|
|
|
||||||
|
2πkT |
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|||
*C) можно, заменив υ2 на |
|
2ε |
|
и dυ на |
|
dε |
|
в выражении f(υ)dυ; |
|||||||||
|
|
|
|
|
|||||||||||||
|
m |
2mε |
|||||||||||||||
(!) 69. f(x2) – некоторая функция случайной величины x. Интеграл
+∞
∫ f (x2 ) α exp( −αx2 )dx равен: f (x2 ) ;
π
−∞
70. Отношение интегралов для молекулы водорода Н2 (молярная масса водорода 2 10-
|
+∞ |
|
|
|
|
∫εf (ε)dε |
|
3кг/моль) при Т=300 К с учетом NA≈6 10231/моль |
|
0 |
= A 10 B , где A и B – |
+∞ |
|
||
∫υx2 f (υx )dυx
−∞
целые числа, значения которых перечислите через точку с запятой … , … без учета размерностей. (*Ответ: 5; -19)
(!) 71. Отношение максимальных значений функций распределения для молекул
идеального газа |
f2 max (ε ) |
= |
1 |
. При этом отношение наиболее вероятных значений |
|
f |
(ε ) |
4 |
|||
|
1max |
|
|
|
|
ε2нв = ... (*Ответ: 4)
ε1вн
εнв
(!) 72. Для молекул идеального газа значения интегралов I1 = ∫ f (ε)dε и
0
∞
I2 = ∫ f (ε)dε , где εнв - наиболее вероятная энергия:
εнв
*B) I1<I2;
(!) 73. Для классической функции распределения по модулю скорости при условии
f (υ2 )dυ
Т=const, а υ2>υ1 отношение f (υ1)dυ ;
*D) >1, если υ1 и υ2 меньше υнв; *E) <1, если υ2 и υ1 больше υнв ;
(!)74. Для данного газа в равновесном состоянии отношение средней энергии частиц к наиболее вероятной энергии при заданной температуре равно…
(*Ответ: 3)
(!)75. Если f(υx) – функция распределения молекул идеального газа по проекции
+∞ +∞
скорости, то для интегралов: I1 = ∫υx f (υx )dυx , I2 = ∫υx2 f (υx )dυx ,
−∞ −∞
+∞
I3 = ∫υx3 f (υx )dυx справедливо следующее соотношение:
−∞
*D) I1 = I3 = 0; I2 > 0;
(!) 76. При T=const максимальное значение функции распределения по проекции импульса f(px):
*D) m1 ;
(!) 77. Значения функций распределения по проекции скорости при υх , равной наиболее вероятной υхнв , для газов с молярными массами М1 и М 2 соответственно
равны: f1(υхнв ) =1,8 10 −3 ; f2 (υхнв ) = 0,6 10−3 . С учетом T=const отношение |
М1 |
= .... |
|
М 2 |
|||
|
|
(*Ответ: 9)
