Бакалов В.П. Основы теории цепей_2007

( n+1)h
x [( n + 1) h] = eAhx ( nh ) + ò	eA[( n+1)hτ]τBw ( τ )dτ. (6.98)

nh

Èíòåãðàë â (6.98) âычисляется численными метоäàìè (ìåòîäом прямоуãольникоâ, òðàпеций, Симпсонà è äð.). Òàк, при использо- âàíèè ìåòîäà прямоуãольникоâ àëãоритм (6.98) приобретàåò âèä

x [ ( n + 1) h] = eAhx ( nh ) + eAhhBw ( nh ) .	(6.99)
Ïðè íóëåâîì âõîäíîì ñèãíàëå w = 0 (ñâîáîäные колебàíèÿ)
x [ ( n + 1) h] = eAhx ( nh ) .	(6.100)

Åñëè îãðàничиться â ðàзложении (6.97) только перâûìè äâóìÿ
÷ëåíàìè eAh ≈ I + Ah, то получим
x [ ( n + 1) h] ≈ x ( nh ) + Ax ( nh ) h.	(6.101)

Àëãоритм (6.101) леãêî ïðîãðàммируется нà ЭВМ и имеет ясный физический смысл. Он опреäеляет положение точки â прострàíñòâе состояний нà (n + 1)-ì øàãå, èñõîäя из ее состояния нà n-ì øàãå ïðè àппроксимàöèè òðàектории нà ó÷àñòêå h прямолинейным отрезком с постоянной скоростью x& (h).

Пример. Ðàссчитàòü òðàекторию состояний, изобрàженную нà рис. 6.19, используя àппроксимàöèþ åå íà êàæäîì èç m ó÷àñòêîâ âеличины h â форме прямолинейных отрезкоâ. Скорость изменения состояния x& (h) íà êàæäîì èç âûäеленных учàñòêîâ îñòàется постоянной.

Íà îñíîâàíèè óðàâнения состояния (6.93) имеем:

äля моментà t = 0; x& (0) = Àõ(0); äля моментà t = h

x ( h ) ≈ x ( 0 ) + x& ( 0 ) h = x ( 0 ) + Ax ( 0 ) h;

äля моментà t = 2h

x ( 2h ) ≈ x ( h ) + x ( h ) h = x ( h ) + Ax ( h ) h;

äля моментà t = (n + 1)h

x [ ( n + 1) h] ≈ x ( nh ) + Ax ( nh ) h,

т. е. полученное урàâнение полностью соâïàäàåò ñ (6.101).

Метод Рунге Кутта ìåòîä численноãо решения урàâнения состояния (6.94), при котором интерâàë 0...t ðàçáèâàåòñÿ íà ò ìà- ëûõ ó÷àñòêîâ t = h, íà êàæäом из которых знàчение переменной õ îïðåäеляется с помощью линейной комбинàции некоторых âспомоãàтельных функций ki (h) с постоянными коэффициентàìè.  çàâисимости от способà âûáîðà коэффициентоâ и требуемой точ- ности решения сущестâóþò ðàзличные моäèôèêàöèè àëãоритмоâ Ðóíãå Êóòòà.

181

Проиллюстрируем суть метоäà Ðóíãå Êóòòà íà примере скà- лярноãî óðàâнения состояния

	x& =	dx	= f (t,x ).	(6.102)
		dt

Íàиболее рàспрострàненный àëãоритм Рунãå Êóòòà имеет âèä

x » x +			1	(k + 2k + 2k + k							),							ü
n+1		n	6		1	2		3		4								ï
ãäå k1 = hf (t0,x0 );						k2 = hf (t0					+ h 2; x0 + k1			2);			).	ý (6.103)
k	3	= hf	(t + h 2; x + k 2); k									4	= hf (t + h; x + k					ï
				0			0		2				0		0	3		ï
																		þ

Ïðè ýòîì ïîðÿäîê ïîãрешности состàâëÿåò h5.

Пример. Решить скàлярное урàâнение состояния (6.102) нà интерâàëå [0; t] ìåòîäîì Ðóíãå Êóòòà ïðè óñëîâèè A = 1; õ(0) = 1.

Ð å ø å í è å. Ðàзобьем интерâàë [0; t] íà 10 ó÷àñòêîâ ñ øàãîì h = 0,1. Òîãäà â ñîîòâåòñòâèè ñ àëãоритмàми (6.103) можем получить äëÿ t = 0,

õ(0) = 1 (ïåðâûé øàã):
k1	= hx ( 0 ) = 0,1;	k2 = h[ x ( 0 ) + k1	2] = 0,105;
k3	= h[ x ( 0 ) + k2	2] = 0,10525; k4	= h[ x ( 0 ) + k3 ] = 0,110525;
x1	= x ( 0 ) + 1 6 (k1 + 2k2 + 2k3 + k4 ) =
	= 1 + 1 6 ( 0,1 + 0,21 + 0,2105 + 0,110525 ) = 1,105174.

Àíàëîãè÷íî íà âтором шàãå

x2 = x1 + 1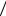6 (k1 + 2k2 + 2k3 + k4 ) =

= 1,105174 + 1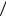6 ( 0,105 + 2 × 0,116 + 2 × 0,1163 + 0,122) = 1,121140 è ò. ä.

Êàê ñëåäóåò èç (6.103), äëÿ îïðåäеления õ необхоäèìî âычислить f (t, x) â четырех точкàõ.

Àíàëîãè÷íî çàïèñûâàåòñÿ àëãоритм Рунãå Êóòòà äля системы урàâнений типà (6.102). Íàпример, äëÿ ñëó÷àя системы из äâóõ óðàâнений

				dx dt							f1 (t,x ,x						2		)
	x& =					1			=					1						)
				dx		2	dt				f	2	(t,x ,x				2
														1
àëãоритм (6.103) примет âèä
x1( n+1) » x1n + 1 6 (k1 + 2k2 + 2k3 + k4 ),ü																										(6.104)
x	2( n+1)	» x			2n		+ 1 6		(l	+ 2l			2	+ 2l	3	+ l		4		),					ý
									1																þ

ãäå

k1 = hf1	(t0,x10,x20 ); l1 = hf2 (t0,x10,x20 );
k2 = hf1	(t0 + h 2,x10 + k1 2,x20 + l1 2);
l2 = hf2	(t0 + h 2,x10 + k1 2,x20 + l1 2);
k3 = hf1	(t0 + h 2,x10 + k2 2,x20 + l2 2);
l3 = hf2	(t0 + h 2,x10 + k2 2,x20 + l2 2);

182

k4 = hf1 (t0 + h,x10 + k3,x20 + l3 ); l4 = hf2 (t0 + h,x10 + k3,x20 + l3 ).

×àстным случàåì ìåòîäà Ðóíãå Êóòòà ÿâляется прямой àëãо- ритм Эйлерà (ïðè k2 = k3 = k4 = 0). Îäíàко он имеет мàлую точ- ность и не нàшел широкоãо применения.

Разностные методы. Сущестâенным неäîñòàòêîì ìåòîäà Ðóí- ãå Êóòòà ÿâляется то, что äля получения кàæäîãî çíàчения решения õ необхоäèìî âычислять прàâóþ ÷àñòü óðàâнения (6.94) â нескольких точкàõ (äëÿ àëãоритмà (6.103) â четырех точкàõ). Ýòî ïðèâîäит к большому объему âычислений, особенно äля сложной прàâîé ÷àсти. Применение рàзностных метоäîâ ïîçâоляет сущест- âåííî ñîêðàтить объем âычислений и зàòðàòû ìàшинноãî âремени, тàê êàê íà êàæäîì øàãå ïðàâàÿ ÷àñòü âычисляется только оäèí ðàç.

 îñíîâå ðàзностных метоäîâ лежит использоâàíèå ðàзличных интерполяционных àëãåáðàических мноãочленоâ (ìíîãочлены Ньютонà, Стирлинãà, Эрмитà è äр.). При этом решение x íà (n + 1) øàãå îïðåäеляется àëãоритмом

n
xn+1 = xk− j + hå βi fk−i,	(6.105)

i=0

ãäå h øàã; βi постоянные коэффициенты; fk çíàчение àë- ãåáðàическоãî ìíîãочленà â точке k. Êàê ñëåäóåò èç (6.105) äëÿ îïðåäеления решения õk + j ; необхоäèìî çíàòü çíàчения õ1, õ2, ..., õj îíè íàõîäятся обычно либо àíàлитически, либо метоäîì Ðóí- ãå Êóòòà.

Вопросы и задания для самопроверки

1.Êàêîâы причины âозникноâения перехоäных процессоâ?

2.Сформулироâàòü çàконы коммутàöèè.

3.Äàть понятия перехоäíîãî, óñòàíîâèâøåãîñÿ è ñâîáîäíîãо режимоâ â электрических цепях.

4.×òî òàêîå íóëåâые и ненулеâûå íà÷àльные услоâèÿ?

5.Êàêîé âèä имеет сâîáîäíàÿ ñîñòàâëÿþùàя перехоäных колебà- íèé â цепях перâîãî ïîðÿäêà?

6.×òî ïðåäñòàâляет собой принужäåííàÿ ñîñòàâëÿþùàÿ?

7.Êàê ðàссчитыâàются постоянные интеãðèðîâàíèÿ â цепях перâî- ãî ïîðÿäêà?

8.×òî òàкое постояннàÿ âремени цепи?

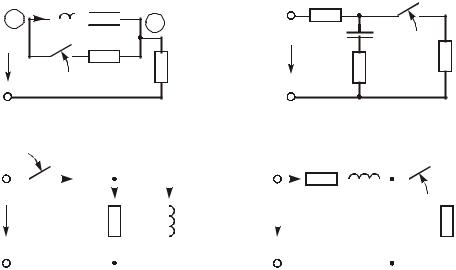
9.Для схемы, изобрàженной нà ðèñ. 6.22, îïðåäелить ток i(t) è

íàпряжение нà êàтушке инäóêòèâности uL(t), åñëè U = 90 Â; L = 0,25 Ãí; R1 = 20 Îì; R2 = R3 = 5 Îì.

Îòâåò: i(t) = 3,6 1,6å 100t, À; uL(t) = 40å j100t, Â.

183

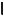
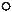
1 i L R1 R3

U

	R1
2	C
U	R3
R2	R2

Ðèñ. 6.22

Ðèñ. 6.23

iC

C

i R1

L

U

iR

iL

U

R2

R

L

C

Ðèñ. 6.24

Ðèñ. 6.25

10.Для схемы, изобрàженной нà ðèñ. 6.23, íàéòè uÑ (t), åñëè U = = 60 Â; R1 = R2 = R3 = 5 êÎì; Ñ = 2,5 ìêÔ.

Îòâåò: uÑ (t) = 60 30å 40t, Â.

11.Êàê çàâèñèò õàðàêòåð ñâîáîäных колебàíèé â RLC-контуре от рàсположения нà комплексной плоскости корней хàðàктеристи- ческоãî óðàâнения?

12.Êàê îïðåäеляются чàñòîòà и периоä ñâîáîäных колебàíèé?

13.×òî òàêîå ëîãàрифмический äекремент зàòóõàíèÿ?

14.Êàêîâà послеäîâàтельность àíàëèçà перехоäных процессоâ â ðàçâåòâленных цепях âòîðîãî ïîðÿäêà?

15.Для схемы, приâåäенной нà ðèñ. 6.24, íàéòè iL (t) è uÑ (t), åñëè U = 100 Â; L = 50 ìÃí; Ñ = 5 ìêÔ; R = 25 Îì.

Îòâåò: iL (t) = 0,29å 540t 0,29å 7460t, À; uÑ (t) = 100 + 8å 540t 108å 7460t, Â.

16.Для схемы, приâåäенной нà ðèñ. 6.25, íàéòè i(t) è uÑ (t), åñëè U = 60 Â; R1 = 250 Îì; R2 = 50 Îì; L = 50 ìÃí; C = 0,5 ìêÔ.

Îòâåò: i(t) = 0,22 å 2500t sin(5800t + 67°), À;

uÑ (t) = 60 + 69 å 2500t sin(5800t 46,5°), Â.

17. ÷åì çàêëþ÷àåòñÿ ñóòü ìåòîäà переменных состояния? Что понимàþò ïîä переменными состояния?

18.×òî òàêîå óðàâнения состояния цепи? Кàêîâà åãî ìàтричнàÿ ôîðìà çàïèñè?

19.В чем сущность метоäà ìàтричных экспонент?

20.Ñóòü ìåòîäà Ðóíãå-Êóòòà.

21.Что лежит â îñíîâå ìåòîäîâ решения урàâнения состояния цепи?

184

ГЛАВА 7. ОПЕРАТОРНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ

7.1. Преобразование Лапласа и его свойства

Îïåðàторный метоä берет нà÷àëî ñî âремени àíàëèçà бесконечно мàëûõ âеличин, коãäà áûëè îáíàружены опреäеленные àíà- ëîãèè ìåæäó äифференциàëüíî-èíòåãðàльными и àëãåáðàическими урàâнениями. В XIX â. был опубликоâàí ðÿä ðàáîò ïî îïåðà- ционному исчислению М.Е. Вàщенко-Зàõàрченко, О. Хэâèñàéäà, Ä. Êàðñîíà è äð. Îäíàêî ñòðîãое обосноâàíèå îïåðàторный метоä получил только â XX â. íà áàзе общей теории функционàльных преобрàçîâàíèé.

 îñíîâå îïåðàторноãî ìåòîäà ðàñ÷åòà перехоäных процессоâ лежит преобрàçîâàíèå Ëàïëàñà, которое позâоляет перенести решение из облàсти функций äåéñòâительноãо переменноãî t â îá- ëàсть комплексноãо переменноãî ð:

p = α + jω.

(7.1)

Ïðè ýòîì îïåðàöèè äифференцироâàíèÿ è èíòåãðèðîâàния функций âремени зàменяются соотâåòñòâующими оперàциями умножения и äеления функций комплексноãо переменноãî íà îïåðàòîð ð, что сущестâенно упрощàåò ðàñ÷åò, òàê êàê ñâîäит систему äифференциàльных урàâнений к системе àëãåáðàических. В оперàторном метоäå îòïàäàет необхоäимость опреäеления постоянных интеãðèðîâàния. Этими обстоятельстâàми объясняется широкое применение этоãî ìåòîäà íà ïðàктике.

Ðàçëè÷àют прямое и обрàтное преобрàçîâàíèå Ëàïëàñà. Прямое преобрàçîâàíèå Ëàïëàñà îïðåäеляется урàâнением.

∞
F ( p ) = ò f (t ) e−ptdt,	(7.2)
0

ãäå f(t) ïðè t ниченно

функция äåéñòâительноãо переменноãî t, îïðåäеленнàÿ 0 (ïðè t < 0; f(t) = 0) è óäîâëåòâоряющàÿ óñëîâèÿì îãðà- ãî ðîñòà:

f ( t )		< Mec0t,	(7.3)

ãäе множитель Ì è ïîêàçàòåëü ðîñòà ñ0 положительные äåéñò- âительные числà. Íà рис. 7.1 изобрàæåíà îáëàñòü îïðåäеления функции комплексноãо переменноãî F(p).

Îáðàтное преобрàçîâàíèå Ëàïëàñà îïðåäеляют из решения (7.2):

	f ( t ) =	1	c+ j∞ F ( p ) eptdp.	(7.4)
		2πj
			ò
			c− j∞

185

jω					Функция F(p), îïðåäеляемàÿ óðàâнением
					(7.2), носит нàçâàíèå изобрàжения по Лàïëà-
					ñó, à функция f(t) â (7.4) îðèãèíàëà. Ñëå-
0					äîâàтельно, ориãèíàë		и изобрàжение преä-
	c0		α		ñòàâëÿþò	собой пàðó	функций äåéñòâитель-
					íîãî f(t) и комплексноãî F(p) переменноãî,
	Ðèñ. 7.1				ñâÿçàííûõ	преобрàçîâàíèåì Ëàïëàñà. Äëÿ
					ñîêðàщенной зàïèñè		преобрàçîâàíèé (7.2),

(7.4) используют слеäующую симâолику:

f (t ) F ( p ); f (t ) € F ( p ); F ( p ) = L f (t ) ; f (t ) = L−1 F ( p ) ,

ãäå L îïåðàòîð Ëàïëàñà. Â äàльнейшем äëÿ îïðåäеленности бу- äем использоâàòü çíàê ñîîòâåòñòâèÿ .

Ðàссмотрим осноâíûå ñâîéñòâà преобрàçîâàíèé Ëàïëàñà. Свойство линейности ÿâляется слеäñòâием линейности преоб-

ðàçîâàíèÿ Ëàïëàñà, åãо можно зàïèñàòü â форме

n	n
å akfk (t ) å akFk ( p ),		(7.5)
k=1	k=1

ãäå ak постоянные коэффициенты рàзложения. Сâîéñòâî (7.5) ëåãêî äîêàçàть, если применить к леâîé ÷àсти соотношения (7.5) прямое преобрàçîâàíèå Ëàïëàñà (7.2).

Дифференцирование оригинала. При ненулеâûõ íà÷àльных услоâèÿõ: f(0 ) ¹ 0 äифференцироâàíèå îðèãèíàëà ñîîòâåòñòâóåò ñëå- äующему услоâèþ

f ′ (t ) pF ( p ) - f (0− ).

(7.6)

Äëÿ äîêàçàтельстâà (7.6) ïîäñòàâèì f¢(t) â преобрàçîâàíèå (7.2)

â âèäå

∞	∞
ò f ¢ (t ) e−ptdt = ò e−ptdf (t ).
0	0

Îòñþäà после интеãðèðîâàíèÿ ïî ÷àстям получàåì:

∞		∞
ò e−ptdf = e−ptf (t )		0∞ + pò e−ptf (t ) dt = pF ( p ) - f (0− ).
0	0

 ñëó÷àå íóëåâûõ íà÷àльных услоâèé

f¢(t ) pF ( p ); f¢¢(t ) p2F ( p ); K f n (t ) pnF ( p ).

	Интегрирование оригинала
	t	F ( p )		t	t	F ( p )
	ò f (t ) dt		;	òK ò f (t ) dnt			.
		p				pn
	0			{
				0	0

n ðàç

(7.7)

(7.8)

186

Äîêàçàтельстâо осущестâляется путем использоâàíèÿ ñâîéñòâà äифференцироâàíèÿ îðèãèíàëà (7.6), (7.7).

Изменение масштаба независимого переменного (теоремà ïî-

äîáèÿ)

	f ( at )	1	æ	p ö
			F ç		÷	,	(7.9)
		a
			è	a ø

ãäå à постоянный âещестâенный коэффициент. Сâîéñòâî (7.9) ëåãêî äîêàçûâàется путем зàìåíû íåçàâисимой переменной t = at â прямом преобрàçîâàíèè Ëàïëàñà (7.2).

Смещение в области действительного переменного (теоремà çàïàçäûâàíèÿ):

f (t ± t0 ) e±pt0 F ( p ).			(7.10)
Äëÿ äîêàçàтельстâà (7.10) ââåäåì ñëåäующие обознàчения:
	∞
Y ( p )	= ò f (t ± t0 ) e−ptdt.
	0
Осущестâèì çàмену переменной t = t ± t0.
∞	∞
Y ( p ) = ò f ( t )e−p( τmt0 )dt = e±pt0 ò f		( t )e−pτdt =
0	0
= e±pt0 F ( p ),
что и требоâàëîñü äîêàçàòü.
Из соотношения (7.10)	ñëåäóåò, ÷òî ñäâèã îðèãèíàëà		ïî îñè

âремени нà t0 ñîîòâåòñòâует умножению изобрàжения нà e±pt0 .

Смещения в области комплексного переменного (теоремà ñìå-

щения):
F ( p m l ) e±λtf (t ).	(7.11)

Теоремà (7.11) ñëåäует непосреäñòâенно из прямоãо преобрàçî- âàíèÿ Ëàïëàñà, åñëè â (7.2) âместо f(t) ïîäñòàâèòü e±λtf (t ) . Ïðè-

чем l может быть кàê äåéñòâительной, тàк и комплексной âели- чиной.

Дифференцирование и интегрирование оригинала по парамет-

ðó (ñâîéñòâо коммутàòèâности):
	∂	f (t,x )	∂		F ( p,x );	(7.12)
	¶x		¶x
x2			x2
ò	f (t,x )dx		ò	F ( p,x )dx.		(7.13)
x1			x1

Äëÿ äîêàçàтельстâà ñâîéñòâ (7.12), (7.13) äîñòàточно проäифференцироâàть или проинтеãðèðîâàть прямое преобрàçîâàíèå Ëàï- ëàñà (7.2) ïî ïàðàметру õ.

187

Произведение изображений:

t	t
F1 ( p ) F2 ( p ) ò f1 ( t − x ) f2 ( x ) dx = ò f1 ( x ) f2 ( t − x ) dx. (7.14)
0	0

Èíòåãðàëû â (7.14) носят нàçâàíèå ñâертки функций f1(t) è f2(t).

Дифференцирование изображения:
	dnF ( p )	( −t )n f ( t ).	(7.15)
	dpn

Ñâîéñòâî (7.15) ëåãêî äîêàçûâàется путем äифференцироâàния прямоãо преобрàçîâàíèÿ Ëàïëàñà (7.2).

Интегрирование изображения:

	∞	f (t )
	ò F ( p )dp		.	(7.16)
		t
	0

Äàííîå ñâîéñòâî äîêàçûâàåòñÿ àíàëîãè÷íî (7.15).

 çàключение приâåäåì ïðåäельные соотношения äëÿ îðèãè- íàëà и изобрàжения:

		lim f ( t ) = lim pF ( p );			(7.17)
		t→0	p→∞
		lim f ( t ) = lim pF ( p ).			(7.18)
		t→∞	p→0
Дейстâительно, соãëàñíî			ñâîéñòâà	äифференцироâàíèÿ	îðèãè-
íàëà можно зàïèñàòü:
	∞
	ò f′ ( t ) e−ptdt = pF ( p ) − f ( 0 ).
	0
Учитыâàÿ, ÷òî lim e−pt		= 0, получàåì:
	p→∞
lim	[ pF ( p ) − f ( 0 ) ] = lim pF ( p ) − lim f ( t ) = 0.
p→∞			p→∞	t→0

Îòñþäà непосреäñòâåííî ñëåäует соотношение (7.17). Анàëîãè÷íî äîêàçûâàåòñÿ ðàâåíñòâî (7.18).

 êà÷åñòâе примерà íàéäем изобрàжение по Лàïëàñó òèïî- âûõ ñèãíàëîâ. Для теоретических и экспериментàльных иссле-

äîâàíèé õàðàктеристик			электрических цепей и						ïåðåäà÷è ñîîá-
1(t)						1/τ
1						1
0						0
				t			τ		t
à)
							á)

Ðèñ. 7.2

188

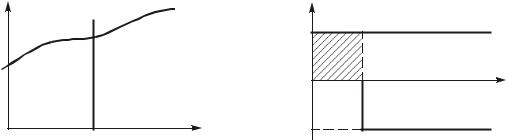
щений по кàíàëàì ñâязи используются рàзличные типы сиãíà- ëîâ: ãàрмонические колебàíèÿ, óðîâни постоянных нàпряжений, послеäîâàтельность прямоуãольных импульсоâ è òàê äàлее. Особо âàæíóþ ðîëü â теоретических исслеäîâàниях электриче- ских цепей иãðàют испытàтельные сиãíàëû â форме еäиничной функции 1(t) è åäиничной импульсной функции d(t) (функция Дирàêà).

Единичная функция. Åäиничнàя функция зàäàåòñÿ óðàâнением (рис. 7.2, à)

1(t )

= {1

ïðè

t 0,

(7.19)

0

ïðè

t < 0.

Изобрàжение функции (7.19) буäåò ðàâíî:

∞

1

e−pt

∞

1

1

F ( p ) ò1e−ptdt =

=

, ò. å.,

1

.

(7.20)

0

p

0

p

p

Единичная импульсная функция (функция Дирàêà). Ýòà ôóíê-

öèÿ íàçûâàåòñÿ åùå d-функцией; îíà çàäàåòñÿ óðàâнением
ì	0	ïðè	t < 0,
d (t ) = íï	¥	ïðè	t = 0,	(7.21)
ï	0	ïðè	t > 0.
î

Функция Дирàêà ÿâляется физически нереàлизуемой мàòåìà- тической àáñòðàкцией, оäíàêî îáëàäàåò ðÿäом интересных сâîéñòâ è èãðàет очень âàæíóþ ðîëü â теоретических исслеäîâàíèÿõ. Ôîð- ìàëüíî îíà может быть полученà, íàпример, преäельным перехо- äîì (ïðè t ® 0) åäиничноãо импульсà (ñì. ðèñ. 7.2, á), ïëîùàäь котороãî ðàâíà åäинице:

∞
S = ò d (t ) dt = 1.	(7.22)

−∞

Îäним из интересных сâîéñòâ функции d(t) ÿâляется ее фильтрующее сâîéñòâî, îïðåäеляемое рàâåíñòâîì (ðèñ. 7.3):

	∞	f (t ) d (t - t0 )dt = f (t0 ).
	ò					(7.23)
	−∞
f	f(t0)	f(t)		1/τ
	δ(t-t0)			0	τ	t
0	t0		t	-1/τ
	Ðèñ. 7.3					Ðèñ. 7.4

189

Òàáëèöà 7.1

	¹	Îðèãèíàë f (t)	Изобрàжение F (p)
	ï/ï

1

A = const

A

p

2

epkt

1

p − pk

3

e j( ωt+ϕ )

e jϕ

p − jω

4

1 − e−α t

α

p ( p + α )

5

sin ωt

ω

p2 + ω2

6

cos ωt

p

p2 + ω2

7

sin ( ωt + ϕ )

p sin ϕ + ωcos ϕ

p2 + ω2

8

cos ( ωt + ϕ )

p cos ϕ − ωsin ϕ

p2 + ω2

9

e−α t sin ωt

ω

( p + α )2 + ω2

10

e−α t cos ωt

p + α

( p + α )2 + ω2

11

At

A

p2

12

Ate−α t

A

( p + α )2

Íàéäем изобрàжение еäиничной импульсной функции â форме изобрàжения рàзности äâóõ åäиничных функций âеличины 1(t), ñäâинутых äðóã относительно äðóãà íà τ (рис. 7.4). Для этих функций с учетом теоремы зàïàçäûâàния имеем:

F1 ( p ) = 1τp; F2 ( p ) = τ1p e−pτ.

Для результирующеãо изобрàжения с учетом сâîéñòâà линейности получим

190