Книга 2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования

Северо-Западный государственный заочный технический университет

Кафедра информатики и вычислительной математики

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

Основы теории вероятностей, элементы математической статистики

Методические указания к выполнению лабораторных работ

Факультеты все Направления подготовки дипломированных специалистов

и отнесенные к ним специальности 650000 – техника и технологии:

Специальности все, кроме 210100, 220100.

Направления бакалавров – 550000 – технические науки,

кроме 550200, 552800

Санкт-Петербург

2004

1

Утверждено редакционно-издательским советом университета УДК 519.2.06(07)

Вычислительная математика. Основы теории вероятностей, элементы математической статистики: Методические указания к выполнению лабораторных работ. – СПб.: СЗГТУ, 2001, - 51 с.

Методические указания предназначены для студентов всех специальностей всех форм обучения и представляют собой руко-водство к выполнению лабораторных работ по разделу “Основы теории вероятностей, элементы математической статистики” курса вычислительной математики.

Содержат описание двух лабораторных работ.

Разработаны на основе рабочей программы по теории вероят-ностей и математической статистике.

Рассмотрено на заседании кафедры информатики и вычисли-тельной математики 5.06.2004 г., одобрено методической комис-сией факультета информатики и систем управления 03.12.2004 г.

РЕЦЕНЗЕНТЫ: Каф. информатики и вычислительной математики Северо-Западного государственного технического университета (зав. кафедрой, канд. физ.-мат. наук, доц. Ткаченко Г.Г.),

Востоков С.В., д-р. физ.-мат. наук, проф. мат.-мех. факультета СПбГУ

СОСТАВИТЕЛИ: В.В. Тарасенко, канд. физ.-мат. наук, доц. Г.Г. Ткаченко, канд. физ.-мат. наук, доц.,

М.Б. Шабаева, канд. физ.-мат. наук, доц.

© Северо-Западный государственный заочный технический университет, 2004.

2

ОБЩИЕ УКАЗАНИЯ Практика решения научно-технических задач в большинстве случаев

приводит к необходимости обработки экспериментальных и статистических данных. Статистические методы позволяют учесть данные опыта для уточнения вероятностной модели, знание которой позволяет прогнозировать будущие события, что важно для принятия решений. Цель выполнения лабораторных работ по курсу “Основы теории вероятностей, элементы математической статистики” – углубление и обобщение теоретических знаний, освоение основных статистических методов и приобретение практических навыков использования MS Excel для обработки статистических данных.

В лабораторных работах рассматриваются следующие типичные задачи математической статистики.

Оценка неизвестных параметров распределения. Задача ставится так:

случайная величина имеет закон распределения определенного вида, зависящий от параметра, значение которого неизвестно. Требуется на основании опытных данных оценить значение этого параметра.

Статистическая проверка гипотез. Одна из основных задач статистической проверки гипотез ставится так: на основании некоторых соображений можно считать, что закон распределения исследуемой

случайной величины f (x). Требуется установить, совместимы ли опытные данные с гипотезой о том, что случайная величина действительно имеет распределение f (x).

Средством решения указанных задач является табличный редактор MS Excel. Одной из целей выполнения работ является освоение возможностей MS Excel для решения сложных статистических задач. К этим возможностям можно отнести мощные и удобные средства анализа данных, составляющие так называемый Пакет анализа, аппарат формул и функций из категории Статистические, графические средства.

В каждой лабораторной работе излагаются необходимые для ее выполнения теоретические сведения, приводятся решения типичных задач и варианты индивидуальных заданий для самостоятельной работы. В приложении приведены необходимые для выполнения лабораторных работ статистические таблицы. Нумерация рисунков и таблиц сквозная, а формулы нумеруются в каждой лабораторной работе автономно.

К выполнению лабораторных работ допускаются студенты, изучившие основные теоретические положения и ознакомившиеся с порядком выполнения работ.

3

ЛИТЕРАТУРА

Основная

1.Захаров В.К., Севастьянов Б.А., Чистяков В.П. Теория вероятностей. –

М.: Наука, 1983.

2.Ильичев В.С., Сланевский А.В. Элементы теории случайных процессов и математической статистики. – Л.: СЗПИ, 1979.

3.Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1999.

4.Рахмина Г.В. Excel 2000. Руководство пользователя с примерами. – М.: Лаборатория Базовых Знаний, 2001.

Дополнительная:

1.Ильичев В.С. Теория вероятностей. – Л.: СЗПИ, 1980.

2.Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения . – М.: Наука, 1988.

3.Сборник задач по математике для втузов. Ч. 3. Теория вероятностей и математическая статистика: Учеб. пособие для втузов/ Под ред. А.В. Ефимова – М.: Наука, 1990.

4.Информатика. Практикум по технологии работы на компьютере. Под ред. В.Н. Макаровой – М.: Финансы и статистика, 1997.

4

Лабораторная работа 1

СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ

1.Цель работы

Изучение методики статистического оценивания параметров закона распределения, освоение инструментов статистического анализа MS Excel.

2.Основные теоретические положения

2.1.Точечная оценка

Если вид закона распределения случайной величины ξ ,

характеризующей генеральную совокупность, известен, то естественно возникает задача оценки (нахождения приближенного значения) параметров, которыми определяется это распределение.

Обозначим неизвестный параметр закона распределения случайной величины ξ через a , а его числовое значение, которое требуется подобрать

по результатам опытных данных, - a*.

Пусть проводится n независимых наблюдений над случайной величиной ξ . Математически такой опыт описывается с помощью выборки.

Выборкой объема n называют n независимых случайных величин	X1,
X 2 , ..., X n , каждая из которых распределена по тому же закону,	что и

случайная величина ξ . Числа x1, x2 , ..., xn , получаемые при однократном

проведении опыта, представляют собой реализацию выборки. Очевидно, при повторном проведении опыта (при повторении n независимых наблюдений) будет получена другая реализация выборки. Оценкой неизвестного

параметра a закона распределения случайной величины ξ	называется
произвольная функция элементов выборки
an* = an* (X1, X 2 ,..., X n ).	(1)

Из соотношения (1) видно, что an* как функция случайных величин

сама также является случайной величиной.

Таким образом, в качестве приближенного значения параметра a , в качестве его точечной оценки, принимают конкретное числовое значение

функции (1) при реализованных значениях выборки X i = xi , i =1,..., n ,

т.е. полагают, что a ≈ an* (x1, x2 ,..., xn ).

Для вычисления значения оценки могут быть использованы различные функции. Чтобы оценку можно было считать хорошим приближением к неизвестному параметру, она должна обладать свойствами несмещенности и состоятельности.

5

Оценка	an	* называется	несмещенной оценкой параметра a , если ее
математическое		ожидание	равно оцениваемому					параметру,	т.	е.
M [an* ]= a .	an* называется
Оценка				состоятельной оценкой				параметра	a ,	если
при n → 0		P{			an * −a		<ε}→1
для любого ε > 0.

Свойство несмещенности означает, что оценка не имеет систематической ошибки. Свойство состоятельности обеспечивает сближение оценки с измеряемым параметром при увеличении числа измерений n .

Состоятельной несмещенной оценкой математического ожидания генеральной совокупности служит выборочное математическое ожидание

*

1

n

m

=

∑ X

i

.

(2)

ξ

n i=1

Выборочная дисперсия

* )2

1

n

D

* =

∑(X

i

− m

(3)

ξ

n i=1

ξ

является смещенной оценкой дисперсии генеральной совокупности. Несмещенной и состоятельной оценкой дисперсии является величина

	s 2 =	1	n	(X		− m * )2 .
			∑		i		(4)
		n −1i=1				ξ

Заметим, что формулы (3) и (4) отличаются лишь знаменателем, и при больших значениях n выборочная и несмещенная дисперсии отличаются

мало. Однако при малом объеме выборки (n < 30) следует пользоваться

соотношением (4).

Оценка среднего квадратического отклонения (стандартного

отклонения), характеризующего наряду с дисперсией			рассеяние значений
случайной величины ξ , определяется формулой
σ	* =	D * .	(5)
	ξ	ξ

Для малых выборок оценку стандартного отклонения вычисляют по формуле:

s = s 2 .

(6)

6

Как отмечалось выше, оценка an* параметра a представляет собой

случайную величину. Разброс ее значений характеризуется дисперсией. На практике дисперсию оценки отождествляют с ошибкой оценки, а среднее квадратическое отклонение оценки называют стандартной (или средней) ошибкой. Таким образом,

стандартная ошибка оценки a* определяется формулой

μa* = D(a* ) .

Вкурсе статистики доказывается, что оценка математического

ожидания нормально

распределенной

случайной

величины

ξ ,

определяемая формулой

(2),

имеет

нормальный закон

N (m ,

σ 2

)

(с

n

2

математическим ожиданием

m

и

дисперсией

σ

).

Следовательно,

n

стандартную ошибку этой оценки следует вычислять по формуле

μ

=

σ

2

(7)

m

*

.

n

2.2.Интервальная оценка

Наряду с точечной оценкой в статистике используется интервальная оценка неизвестного параметра закона распределения случайной величины ξ , которая дает представление о точности и надежности оценки.

Точечная оценка a* является случайной величиной и отличается от постоянного истинного значения параметра a . Обозначим точность оценки (которую также называют предельной ошибкой) через ε (ε > 0) , тогда

a − a* ≤ ε . Доверительной вероятностью (надежностью) называют

вероятность β , с которой осуществляется неравенство a − a* ≤ ε , т. е.

	P(	a − a*						≤ ε)= β .	(8)
Заменив	неравенство			a − a*				≤ ε равносильным ему	двойным
неравенством	−ε ≤ a − a* ≤ε , или						a* −ε ≤ a ≤ a* +ε , получим

7

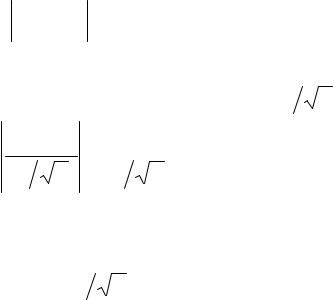
P(a* −ε ≤ a ≤ a* +ε)= β .		(9)
Доверительным называют	интервал I β = (a* −ε;a* +ε),	который
покрывает неизвестный параметр с заданной надежностью β .		Точность
оценки ε определяет длину доверительного интервала.
Вероятность α =1 − β	называется уровнем значимости и

характеризует относительное число ошибочных заключений в общем числе заключений.

Доверительный интервал для математического ожидания нормального

распределения при известной дисперсии.				Предположим, что	случайная
величина ξ	в генеральной совокупности распределена по нормальному
закону N (m,σ 2 ) с		неизвестным	математическим ожиданием m и
известной	дисперсией	D = σ 2 .	Оценку	математического	ожидания

вычислим по формуле (2). Доверительный интервал, соответствующий надежности β , определяется из условия (8), которое в нашем случае имеет вид

P(m* − m ≤ε)= β .

Введем

новую

случайную

величину

m* − m

.

σ

n

*

*

− m

ε

m

−m

m

≤ε и

≤

≡ zβ

эквивалентны,

σ

n

σ

n

соотношение (10) можно записать в виде

(10)

События

поэтому

m

*

− m

P

≤ z

β

= β .

(11)

σ

n

Поскольку, как отмечалось выше, оценка

m* имеет

нормальный закон

распределения N (m,

σ 2

), то введенная случайная величина также имеет

n

нормальный закон N (0,1) (с математическим ожиданием 0 и дисперсией,

равной 1), а значит, вероятность в левой части формулы (11) можно выразить через нормальную стандартную функцию распределения:

8

m

*

− m

= 2Φ(z

)−1.

P

≤ z

β

(12)

σ

n

β

Приравняв правую часть формулы (12) заданной доверительной вероятности

	β , получим	уравнение	Φ (z β )=		1 + β		.		Корень этого	уравнения zβ
				2
	называется	квантилью	порядка		1 + β				стандартного	нормального
						2

распределения и определяется из таблиц. Предельная ошибка ε

вычисляется по формуле	ε =	σ	z β .	Таким		образом,		доверительным
		n							β ,
интервалом математического ожидания, соответствующим надежности
является интервал
I β = (m* −ε, m*				σ	zβ	, m* +	σ		(13)
	+ε)= m* −			n			n	zβ .

Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии. Пусть случайная величина ξ в

генеральной совокупности распределена по нормальному закону N (m,σ 2 ) с неизвестным математическим ожиданием m и неизвестной дисперсией

D = σ 2 . Несмещенные оценки параметров	m и σ 2 вычисляются по
формулам (2) и (4).
Введем новую случайную величину m * − m . Как показано в курсе
s	n

статистики, эта случайная величина распределена по закону Стьюдента, который не зависит от неизвестных параметров, а зависит только от числа наблюдений n . Напомним, что k = n −1 называется числом степеней свободы закона Стьюдента. Рассуждая аналогично случаю, когда дисперсия известна, получим следующий доверительный интервал для математического ожидания:

I β		s	tβ , m* +	s		(14)
	= (m* −ε, m* +ε)= m* −	n		n	tβ .
Замечание 1. В отличие от формулы (13) в формуле (14) используется
оценка s	вместо точного значения σ , а tβ определяется по					таблице

распределения Стьюдента, а не по таблице стандартного нормального закона распределения.

9

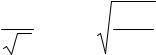
Замечание 2. Поскольку с увеличением числа степеней свободы k распределение Стьюдента быстро приближается к нормальному, то для

больших выборок (n > 30) доверительный интервал для математического ожидания находят по формуле (13), подставляя в качестве σ оценку s .

Пример. По выборке объема n =10, извлеченной из нормальной генеральной совокупности, найдены оценка математического ожидания

m * = 3,62 и несмещенная дисперсия s2 =0,61. Найти доверительный

интервал для математического ожидания, соответствующий доверительной вероятности β = 0,90 .

Решение. Доверительный интервал для математического ожидания определяется по формуле (14). По таблице А приложения для β = 0,90 и

n −1 = 9 находим tβ		=1,83.	Точность оценки математического ожидания
равна
ε = t β	s	= 1,83	0,61 = 1,83 0,247 = 0,45 .
	n		10
Подставляя m* и ε	в формулу (14), находим доверительный интервал для
математического ожидания
I β	= (3,62 − 0,45 ;3,62 + 0,45 )

или I β = (3,17 ;4,07 ).

3.Порядок выполнения лабораторной работы

Лабораторная работа состоит из двух частей. Первая часть включает в себя выполнение заданий 1 и 2 и представляет собой контрольный пример, решение которого приведено ниже. Во второй части самостоятельно выполняется индивидуальное задание, включающее задания 3 и 4.

Задание 1. 1.1. Получить с использованием Пакета анализа выборку объема n = 40 из генеральной совокупности, в которой случайная величина ξ распределена по нормальному закону с параметрами m = 4 и σ = 0,5.

1.2. Найти точечные оценки математического ожидания, дисперсии, стандартного отклонения, а также стандартную ошибку оценки

математического ожидания а) по данным малой выборки (n = 20); б) по данным большой выборки (n = 40).

Задание 2. 2.1. Найти доверительные интервалы, соответствующие доверительной вероятности β = 0,95, для оценок математического ожидания, полученных в задании 1.2, без использования MS Excel.

10