4.6. Вектор-интеграл лапласа
Поле 
допускает существование векторного
интеграла движения, специфического
именно для этого поля. Этот вектор был
построен еще Лапласом. Мы будем называть
его вектором Лапласа, хотя в квантовой
механике аналогичный векторный оператор
принято называть вектором Рунге-Ленца.
Докажем, что вектор
являемся интегралом
движения. Для этого вычислим 
:
(26.4)
Подставив в (26.4) выражение
и используя
уравнения движения частицы в поле 
в виде
нетрудно показать,
что 
,
т. е. 
.
Из равенства нулю
скалярного произведения 
следует, что вектор 
перпендикулярен 
и лежит в плоскости орбиты. Направление
вектора 
найдем, воспользовавшись законом
сохранения 
.
Вычислим 
в момент нахождения частицы в точке 
.
Полярную ось направим из фокуса к 
.
В декартовой системе координат с осью
Ox, направленной
по полярной оси, и Оz
- по 
,
получим
.
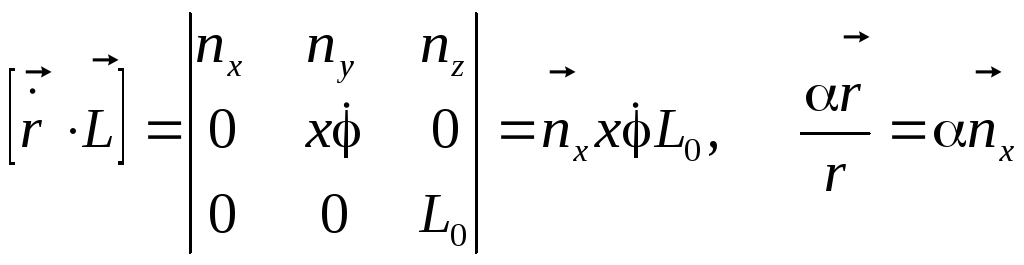Следовательно, 
,
т. е. 
направлен от фокуса (центра силы) в
ближайшую точку траектории. Модуль
вектора 
равен
.
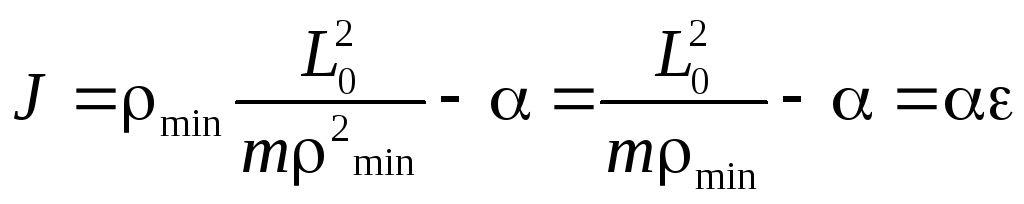Заметим, что
интеграл движения 
является однозначной функцией
механического состояния частицы. Мы
знаем, что в поле 
такими однозначными функциями положения
и скорости частицы являются (кроме 
)
интегралы движения 
и 
.
Появление такого дополнительного
однозначного интеграла связано с так
называемым вырождением движениям
возможностью решения динамической
задачи в различных координатах.
Пример.
Исследовать движение частицы массы 
в центральном
поле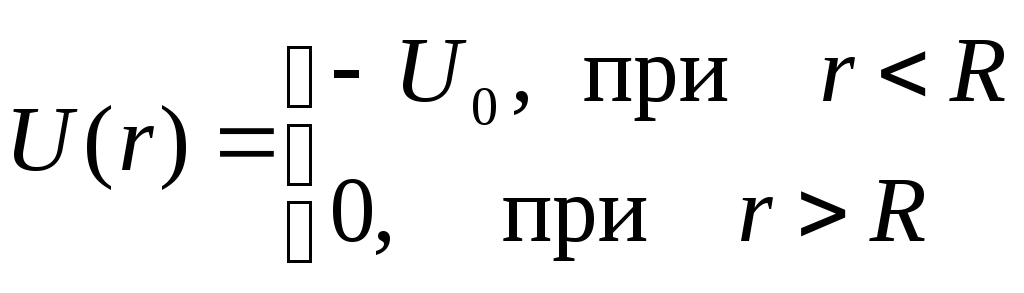 
при различных
значениях энергии и момента импульса
частицы. Поле 
,
которое называют «сферической
прямоугольной потенциальной ямой»,
изображено на рис. 17.4, график эффективной
энергии дан на рис. 18.4.
Рис. 17.4
Эффективная энергия частицы имеет вид
при 
,
при 
.
Поэтому в области
траектория частицы определяется
интегралом (16.4). Это прямая, отстоящая
от центра поля на расстоянии 
.
Из рис. 18.4 видно, что если 
,
и 
то траекторией частицы всегда будет
прямая.
При 
и энергии, заключенной в интервале
,
частица движется
внутри сферы, испытывая отражения на
границе при 
.
Скорость
частицы постоянна и определяется из
закона сохранения механической энергии
.
Записав его в виде
,
находим точку поворота:
.
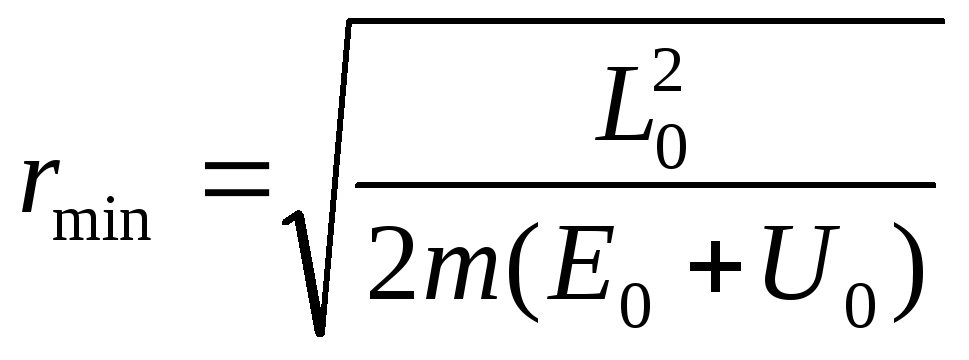Для частицы с
энергией 
точка 
представляет собой непроницаемый
барьер, от которого она отражается.
Между двумя точками отражения частица
движется по отрезку прямой (рис. 19.4)
.
Рис. 19.4 Рис. 20.4
На сфере 
происходит отражение частицы, так что
ее скорость меняет направление на угол,
равный 
,
где
.
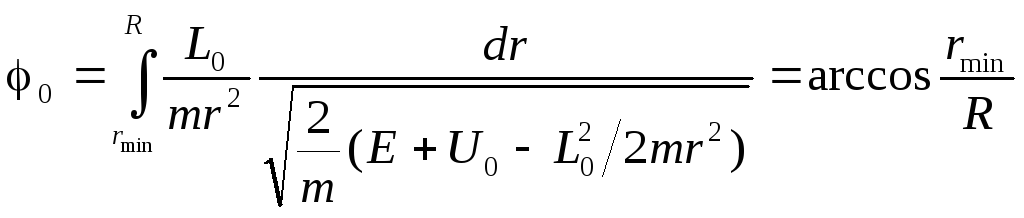Условие замкнутости
траектории 
,
или
.
При выполнении этого условия траекторией частицы является замкнутая ломаная линия.
При 
частица движется в инфинитной области.
Вне сферы радиуса 
частица движется по прямой
,
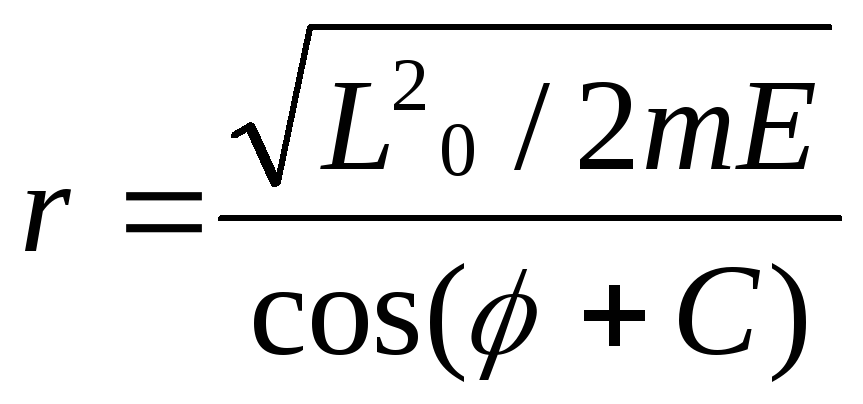а внутри сферы - также по прямой (рис. 20.4)
.
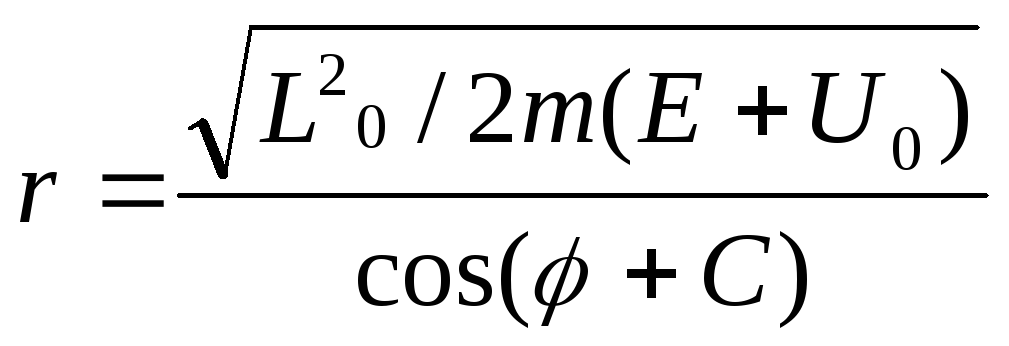Следовательно, имеет место преломление траектории частицы на угол
.
Для определения
угла преломления удобно выбрать 
.
1Общее решение задачи динамики материальной точки должно определяться функциями вида (16.2), зависящими от времени и от шести независимых произвольных постоянных интегрирования, выбором которых можно удовлетворить любым начальным условиям.
Более подробно об этом рекомендуем прочесть в книге: Хакен Г. Синергетика. М.: Мир, 1985.
2Это уравнение конического сечения с фокусом в начале координат. Фокус - это точкаF, лежащая в плоскости кривой второго порядка и такая, что отношение расстояния любой точки кривой доF к расстоянию до заданной прямой (директрисы) равно постоянному числу (эксцентриситету). Конические сечения - линии, которые получаются сечением прямого кругового конуса плоскостями, не проходящими через его вершину.