ТоЭ

120

Разложение такой функции в ряд Фурье приводится в справочной литературе и имеет вид

f (ωt ) =		A	+	2A	(sin ωt +	1	sin3ωt +	1	sin5ωt +...),
		2 π			3		5
где ω=	π.
	τ

Дискретный спектр амплитуд рассматриваемых импульсов приведен на рис. 91, б.

Пример 27

В силовой электронике при получении постоянного напряжения из переменного (т.е. при выпрямлении) для оценки качества постоянного напряжения используется показатель, называемый коэффициентом пульсаций kп . Коэффициент пульсаций равен отношению амплитуды низшей гармоники переменной составляющей выпрямленного напряжения к его среднему значению. Определим коэффициент пульсаций для выпрямленного напряжения ud , диаграмма которого приведена на рис. 92.

		u =	2U cos ωt
			ωt
		2π
	π	ud
− π	0	π	ωt
2		2

Рис. 92

Для использования симметрии кривой ud примем начало отсчета времени, как показано на рис. 92. Тогда переменное напряжение можно записать:

			121
u =U	m	sin(ωt + π) =	2U sin(ωt + π) = 2U cos ωt.
		2	2

Период Т кривой выпрямленного напряжения ud в два раза меньше периода Т0 переменного напряжения u . То есть в угловой мере период кривой ud равен π.

Обозначим среднее значение выпрямленного напряжения U d и вычислим его по формуле (56) как постоянную составляющую разложения в ряд Фурье:

	1	T 2	1	π 2
U d =		∫ f (t)dt =		∫ 2U cosωtd(ωt) =
	T
		−T 2	π−π 2

2U	(sinωt)		π 2	=	2	2	U.
π			−π 2		π

Так как частота кривой ud в два раза больше частоты напряжения u , то низшей гармоникой выпрямленного напряжения будет вторая (относительно гармоники переменного напряжения). Обозначим амплитуду второй гармоники выпрямленного напряжения U 2m и вычислим ее с учетом того, что при симметрии кривой относительно оси ординат синусные составляющие разложения в ряд Фурье отсутствуют:

				2	T 2		2	π 2
	U 2m = c2	= a2	=		∫	f (t)cos 2ωtdt =		∫ 2U cos ωt cos 2ωtd(ωt).
				T
					−T 2		π −π 2

С использованием известного из тригонометрии соотношения cosαcosβ = 12 [cos(α −β) +cos(α +β)]

получим:

=

2 2

π 2

1

(cos

ωt + cos3ωt)d (ωt) =

U 2m

U ∫

π

2

−π 2

=

2

U (sin ωt +

sin 3ωt

π 2

=

2

−

2

=

4 2

)

−π 2

U 2

U.

π

π

3π

3

3

Коэффициент пульсаций для рассматриваемой формы кривой выпрямленного напряжения составит величину

k п =	U 2m	=	4	2U		π	=	2	= 0,667.
						2 2U
	U d			3π			3

122

5.2Расчет линейных цепей с несинусоидальными токами

Перед проведением расчетов цепей с несинусоидальной э.д.с. последняя должна быть представлена рядом Фурье. Если несинусоидальная э.д.с. задана аналитически, то разложение осуществляется по формулам (56), если графически — то графоаналитическим методом [1], который здесь не рассматривается.

Согласно принципу наложения, мгновенное значение тока любой ветви схемы равно сумме мгновенных значений токов отдельных гармоник. Аналогично мгновенное значение напряжения на любом участке схемы равно сумме мгновенных значений напряжений отдельных гармоник на этом участке. Расчет производится для каждой из гармоник в отдельности при помощи приемов, изложенных в разделе 3.

Сначала производится расчет токов и напряжений от действия постоянной составляющей э.д.с. После этого производится расчет токов и напряжений от действия первой гармоники э.д.с., затем от второй гармоники э.д.с., от третьей и т.д.

При расчете токов и напряжений от постоянной составляющей э.д.с. необходимо иметь в виду, что падение напряжения на индуктивности L от постоянного тока равно нулю, а также следует иметь в виду, что постоянный ток через емкость С не протекает.

При расчете необходимо учитывать, что индуктивное сопротивление растет прямо пропорционально частоте, поэтому индук-

тивное сопротивление для k-ой гармоники X Lk		в k раз больше,
чем индуктивное сопротивление для первой гармоники X L1 :
X L = ωL;	X Lk = kωL = k X L .	(58)
1	1

Емкостное сопротивление уменьшается с ростом частоты,

поэтому емкостное сопротивление для k-ой гармоники								X Ck в
k раз меньше, чем емкостное сопротивление XC							для первой гар-
					1
моники:					XC
XC =	1	; X Ck =	1	=
					1	.		(59)
			kωC
1	ωC				k

123

Для каждой из гармоник может быть построена своя векторная диаграмма. Но на одной векторной диаграмме откладывать токи и напряжения различных частот, а равно и складывать векторно токи и напряжения различных гармоник недопустимо, поскольку угловые скорости вращения векторов различных частот неодинаковы.

Рассмотрим далее вопрос определения действующих зна-

чений несинусоидальных токов и напряжений.

По определению (см. подраздел 3.1), квадрат действующего значения тока I выражается через мгновенное значение тока i следующим образом:

I 2 =

1 T

∫i2dt.

T

Если ток

0

i = I 0 + I1m sin(ωt + ϕ1) + I 2m sin(2ωt + ϕ2) +...,

то

∞

(kωt +ϕk) +

∞

i2 = I 02 + ∑ I km2 sin2

∑ I pmI gmsin( pωt +ϕp)sin(gωt +ϕg).

k=1

p=0

g=0, p≠g

Но

T

T

∫sin2 (kωt +ϕk)dt =

,

2

0

T

∫

sin( pωt +ϕp)sin(gωt +ϕg)dt = 0.

0

p≠ g

Поэтому

I12m

I 22m

I 32m

I 2 = I 02 +

+

+

+...,

2

или

2

2

I =

I 02 +

I12m

+

I 22m

+... .

2

2

Так как амплитуда k-ой гармоники тока I km

в 2 раз боль-

ше действующего значения k-ой гармоники I k , то

124

	I km2		=	I km		I km	= I k2
2
			2		2
и
I =		I 02 + I12 + I 22 + I 32 +... .						(60)

Следовательно, действующее значение несинусоидального тока равно квадратному корню из суммы квадратов постоянной составляющей тока и действующих значений отдельных гармоник. От сдвигов фаз ϕк действующее значение не зависит.

Аналогичным образом определяется действующее значение несинусоидального напряжения.

Под активной мощностью Р несинусоидального тока понимается сумма активных мощностей отдельных гармоник:

P =U 0I 0 +U1I1cosϕ1 +U 2I 2 cosϕ2 +....

Полная мощность S равна произведению действующего значения несинусоидального напряжения на действующее значение несинусоидального тока:

S = UI,

где I определяется по (60), U — по аналогичной формуле.

В ряде случаев, например при изучении некоторых простейших свойств нелинейных электрических цепей, несинусоидальные токи и напряжения заменяют эквивалентными синусоидальными. Замена производится таким образом, что действующее значение синусоидального тока принимается равным действующему значению заменяемого несинусоидального тока, а действующее значение синусоидального напряжения берется равным действующему значению несинусоидального напряжения.

Угол сдвига фаз ϕэ между эквивалентными синусоидами

напряжения и тока берется таким, чтобы активная мощность эквивалентного тока была равна активной мощности несинусодального тока:

cos ϕэ = P .

UI

125

Для того чтобы характеризовать форму несинусоидальной функции, используется ряд показателей. Наиболее распространены следующие: коэффициент формы (см. подраздел 3.1), коэффициент амплитуды, коэффициент искажения, коэффициент гармоник. Дадим их определения на примере токов.

Коэффициентом амплитуды называется отношение мак-

симального значения функции к действующему значению:

k a = imax .

I

К примеру, для синусоидальных функций k a = 2. Коэффициентом искажения называется отношение дейст-

вующего значения основной гармоники функции к действующему значению всей функции:

k и = I1 . I

Для синусоидальных функций I1 = I , следовательно, k и = 1. Коэффициентом гармоник называется отношение действующего значения высших гармоник к действующему значению

основной гармоники:

	∞
	∑ I k2
k г =	k =2	.

I1

Для синусоиды k г = 0.

5.3Резонансные явления при несинусоидальных токах

Как известно из подраздела 3.6, резонансным режимом работы электрической цепи, содержащей одну или несколько индуктивностей и одну или несколько емкостей, называют такой режим работы ее, при котором ток на входе этой цепи совпадает по фазе с действующей на входе э.д.с.

126

Если воздействующая э.д.с. несинусоидальна, то в электрической цепи могут возникать резонансные режимы не только на первой гармонике, но и на высших гармониках.

Условимся под резонансом на k-й гармонике понимать такой режим работы, при котором ток k-й гармоники на входе цепи по фазе совпадает с k-й гармоникой действующей на входе э.д.с. (но при этом токи остальных гармоник не совпадают по фазе с вызвавшими их э.д.с.).

При возникновении резонансного и близкого к нему режима на какой-либо высшей гармонике токи и (или) напряжения этой гармоники могут оказаться большими, чем токи и напряжения первой гармоники на тех же участках цепи, несмотря на то, что амплитуда соответствующей высшей гармоники э.д.с. на входе схемы может быть в несколько раз меньше амплитуды первой гармоники э.д.с.

Исследование резонансных явлений при несинусоидальных токах часто производят, полагая активные сопротивления дросселей нулевыми (в контурах, содержащих только конденсаторы и дроссели, но не содержащих резисторов). В таком случае входное сопротивление контура при резонансе токов равно бесконечности, а при резонансе напряжений — нулю.

Пример 28

	С1	L	В схеме на рис. 93 задана индук-
			тивность L. Полагая активное сопро-
			тивление	дросселя нулевым, найти,
		С2	при каких значениях емкостей С1 и С2
			входное	сопротивление схемы для

		первой гармоники равняется нулю, а
	Рис. 93	для девятой гармоники равно беско-
		нечности.
	В соответствии с условиями задания составим систему двух
	уравнений:

127

− j

jωL

− j

ωC

Z1 =

+

2

= 0

ω

1

C1

j ωL −

ω

C

2

− j

j9ωL

− j

9ωC

2

Z 9 =

+

= ∞

9ω

1

C1

j 9ωL −

9ω

C

2

Решим полученную систему уравнений.

1

+

Lω

= 0

ωC1

2

−1

ω LC 2

1

9Lω

.

+

= ∞

9ωC1

2

−1

81ω LC 2

2

2

ω LC 2

+ ω LC1 =1

(81ω2 L

−1)9ω

=

.

C 2

0

C1

.

(а)

Последнее уравнение получено из уравнения (а) после приведения его к общему знаменателю и приравнивания последнего к нулю.

	81ω2 LC 2 =1; C 2 =					1	;
					81ω2 L
	C1	=	80	.
			81ω2 L

Пример 29

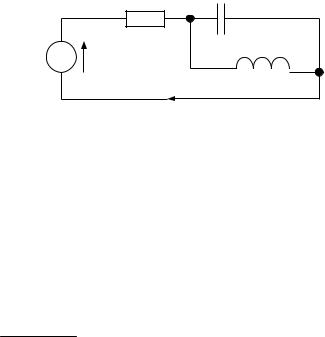
Для схемы на рис. 94 задано: R = ωL = 3 Ом; 1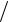ωС = 27 Ом; e(t) =100 +80sin(ωt +30 ) +60sin(3ωt + 20 ) +50sin(5ωt + 45 ) В.

	128
R	b C
	L
~ e(t)	c
	i
	Рис. 94

Требуется определить эффективные значения тока i и э.д.с. е. Рассчитаем комплексное сопротивление участка bc для пер-

вой, третьей и пятой гармоник:

Z

Z

Z

bc1

bc3

bc5

=	3 j(−27 j)	=	81	= j3,38 Ом;
	−27 j +3 j		−24 j

=9 j(−9 j) = ∞ (на третьей гармонике резонанс токов);

−9 j +9 j

=	15 j(−5, 4 j)	=	81	= − j8, 44 Ом.
	15 j −5, 4 j		j9,6

Полное сопротивление цепи для соответствующих гармоник:

Z1 = R + Z bc1 = 3 + j3,38 = 4,52e j48,41		Ом;
Z 3 = R + Z bc3 = ∞;
Z 5	= R + Z bc5 = 3 − j8, 44 = 8,96e− j70,43	Ом;
Z 0	= R = 3 Ом.

Составляющие тока в неразветвленной части схемы:

	I 0	=			100	= 33,3 А;
			3
			80				j30
	I1 =					e			=17,7e− j18,41		A;
			4,52e j48,41
	I 3 = 0;
	I 5	=		50e j45						= 5,58 j115,43	A.
				8,96e			− j70,43			e

129

Мгновенное значение тока в неразветвленной части схемы:

i(t) = 33,3 +17,7sin(ωt −18, 41 ) +5,58sin(5ωt +115,43 ) A.

Искомые эффективные значения величин:

I = 33,32 +17,72 + 5,582 = 35,8 A;

2				2
E = 1002 +	802	+	602	+	502	=127,5 В.
2		2		2

5.4Особенности работы трехфазных систем, вызываемые гармониками, кратными трем

Э.д.с. генератора могут быть искажены, то есть могут быть несинусоидальными. Будем считать, что каждая из э.д.с. фаз повторяет по форме остальные со сдвигом на 1/3 периода.

При разложении в ряд Фурье k-я гармоника фазы А равна: ekA = Ekm sin(kωt +ϕk).

Э.д.с. фазы В отстает от э.д.с. фазы А на Т3, поэтому

		T				k +ϕk).
ekе = Ekm sin kω t −				+ϕk	= Ekm sin(kωt −120
		3

Последняя форма записи получена с учетом того, что

kωT = k 2π T = k 2π =120 k. 3 T 3 3

Э.д.с. фазы С опережает э.д.с. фазы А на Т3, следовательно,

		T				k + ϕk ).
ek„ = Ekm sin kω t +				+ϕk	= Ekm sin(kωt +120
		3

Таким образом, третьи (и кратные трем) гармоники во всех трех фазах совпадают по фазе.

Далее обсудим особенности работы трехфазных систем, вызываемые гармониками, кратными трем.