vm3

сто встречаются функции этого класса, обладающие дополнитель-

	ной симметрией на (0, l) либо относительно прямой x =			l	, либо от-
				2
	носительно точки	l	, 0 . Такие функции называются функциями
		2

с двойной симметрией. Ряд Фурье функций с двойной симметрией несколько упрощается по сравнению с чётными или нечётными функциями. Предлагается в виде упражнения доказать следующие утверждения.

Если функция f (x) периода 2l чётная и обладает дополнительной

симметрией на (0, l) относительно прямой x =						l	, т.е. если f (l − x) =
						2
= f (x), то bn = 0 (n = 1, 2, . . .), a2n+1 = 0 (n							= 0, 1, 2, . . .), a2n =
4		l/2		nπx
=		Z0	f (x) cos	2	dx, n = 0, 1, 2, . . ..
	l			l

Если же чётная функция f (x) симметрична на (0, l) относитель-

но точки

2 , 0 , т.е. если f (l − x) = −f (x), то bn = 0 (n = 1, 2, . . .),

l

4

l/2

+ 1)πx

a2n = 0 (n

= 0, 1, 2, . . .),

a2n+1 =

Z0

f (x) cos

(2n

dx,

l

l

n = 1, 2, . . ..

нечётна на (−l, l)

Если функция f (x)

и симметрична на (0, l)

относительно прямой x

=

l

, то an

= 0 (n = 0, 1, 2, . . .), b2n = 0

2

4

l/2

(2n + 1)πx

Z0

(n = 1, 2, . . .),

b2n+1 =

f (x) sin

dx.

l

l

Для нечётной функции f (x), симметричной на (0, l) относи-

тельно

точки

2 , 0 ,

имеем

an = 0, b2n+1 = 0, n = 0, 1, 2, . . .,

l

4

Z0

l/2

2nπx

dx,

n = 1, 2, . . ..

b2n =

f (x) sin

l

l

Мы рассмотрели разложение в тригонометрический ряд Фурье функции, заданной на промежутке [−l, l], симметричном относительно начала координат. Если же функция задана на [0, l], то её можно доопределить на участке [−l, 0], а затем разложить в ряд Фурье

по известным формулам. Это доопределение можно сделать многими способами. Наиболее часто доопределяют чётным образом, чтобы функция после продолжения была чётной, или нечётным, тогда полученная функция будет нечётной. Практически при этом никаких дополнительных операций совершать не нужно, а пользоваться

141

сразу либо формулами (6.24), либо (6.25). В обоих случаях найден-

ный ряд будет сходиться в точках непрерывности функции f (x) на

(0, l) к f (x). В некоторых случаях доопределение чётным образом

предпочтительнее,

так

как

при

нечётном

продолжении,

если

f (0) 6= 0, добавляется точка разрыва в нуле, что ухудшает качество

сходимости полученного ряда, как мы увидим позднее.

Для периодической функции f (x) с периодом 2l очевидно со-

отношение Z0

2l f (x)dx =

Zaa+2l f (x)dx при любом a. Поэтому, ес-

ли функцию f (x), заданную на [a, a + 2l], разлагают в ряд Фурье,

продолжив её на всю ось с периодом 2l, то коэффициенты an и bn

1

2l

nπx

можно2lвычислять по формулам

Z0

dx, bn =

an

= l

f (x) cos

l

1

nπx

= l Z0

f (x) sin

l

dx.

Пример 6.3. Функцию f (x), график которой изображён на рисун-

f (x) 6

ке, разложить в ряд Фурье:

а) по синусам,

1

б) по косинусам.

Решение. В нашем случае l = 2.

Доопределим функцию f (x) на

-

[−2, 0): а)

нечётным

образом;

O

1

2

x

б) чётным образом. В результате

получим

функции,

заданные на

отрезке [−2, 2], графики которых приведены на рисунках а) и б).

а)	f (x)	6	б)		f (x) 6
	1				1
−2 −1			-	−1			-
		O 1	2 x −2		O	1	2 x
		−1

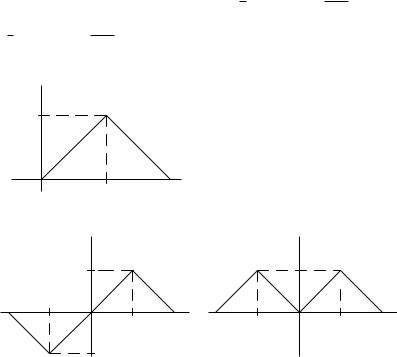
В случае а) функция f (x) нечётна, а график её на (0, 2) симметричен относительно прямой x = 1. Поэтому an = 0 (n = 0, 1, . . .),

142

4

1

(2n + 1)πx

= 0, 1, . . .),

а

Z0

b2n

= 0

(n

b2n+1 =

1x sin

dx

=

2

2

= 2

(2n−+ 1)π cos

(2n

2

0 +

(2n + 1)π Z0

cos

2

dx

=

2x

+ 1)πx

1

2

(2n + 1)πx

(2n + 1)

1

=

8

2

2 sin

=

8

2 2

sin

+ nπ

=

πx

n

π

(2n + 1) π

2

(2n + 1) π

2

8(

8

0

1)

=

cos nπ =

−

2

. Таким образом, в случае а) име-

2

π

2

2

(2n + 1)

∞

(2n + 1) π

ем f (x) =

8

(−1)n

sin (2n + 1)πx .

X

π2

(2n + 1)2

2

n=0

В случае б) функция f (x) чётна и на (0, 2) её график симметричен относительно прямой x = 1. Поэтому bn = 0 (n = 1, 2, . . .), a2n+1 = 0

4

1

4

1

(n

=

0, 1, . . .), a0

=

Z0

1xdx

= 1,

a2n =

Z0

x cos nπxdx

=

2

2

x

1

1

sin nπxdx

2

1

=

=

=

n

−

2

nπ sin nπx

0 − nπ Z0

n2π2 cos nπx

0

2

2[(

2

2−

.

что

a4m

=

0, a4m+2

=

−

2

1)

1]

4

Видим,

n π

(2m + 1) π

(m = 0, 1, 2, . . .). Таким образом, в случае б) имеем

4

∞

1

X

f (x) = 1 − π2 m=0 (2m + 1)2 cos (2m + 1)πx. Предлагается самостоятельно построить график суммы S(x) ря-

дов для случая а) и б).

6.3.3. Другая форма записи тригонометрического ряда Фурье

Предположим, что функция f (x) на [−l, l] разлагается в ряд Фу-

рье по тригонометрической системе, т.е.

a0

∞

nπx

nπx

(6.26)

f (x) = 2

+ n=1 an cos

l

+ bn sin

l ,

X

1

l

nπx

1

l

nπx

Z−l f (x) cos

Z−l f (x) sin

где an =

dx, bn =

dx. Введём в

l

l

l

l

что cos ϕn

=

an

=

an , sin ϕn =

bn

. Тогда ряд

pbn

=

рассмотрение следующие величины: An

=

an2 + bn2 и угол ϕn такой,

p

an2 + bn2

An

p

an2 + bn2

An

143

(6.26) можно переписать в виде

a0

∞

nπx

nπx

,

f (x) =

+ n=1 An cos ϕn cos

+ sin ϕn sin

2

l

l

или

X

a0

∞

nπx

f (x) =

− ϕn

.

(6.27)

2 + n=1 An cos l

nπx

X

Функцию

An cos

− ϕn

называют гармоническим колебанием

l

Она описывает простейший периодический процесс.

или гармоникой.

πn

Величина

An означает амплитуду гармоники, ωn =

её угловую

l

частоту, ϕn начальную фазу гармоники.

Три величины: An, ωn, ϕn полностью определяют гармонику. Как следует из (6.27), функция f (x) представлена в виде суммы гармони-

ческих колебаний бесконечного числа слагаемых. По этой причине разложение функции в ряд Фурье называют её гармоническим анализом. Гармонический анализ сводится к отысканию величин An, ωn, ϕn. Множество {An} всех чисел An называют амплитудным спектром функции f (x), множество {ωn} её частотным спектром, а множество {ϕn} её фазовым спектром. Разложение функции в

ряд Фурье равносильно отысканию указанных спектров. Этот процесс называют также спектральным анализом функции. По заданной функции f (x) однозначно определяются её спектры и, обратно, по заданным спектрам восстанавливается функция f (x) в виде ряда

(6.27), если этот ряд сходится.

Заметим, что амплитудный, частотный и фазовый спектры функции f (x), представимой в виде суммы тригонометрического ряда Фу-

рье, дискретны. Все они являются счётными множествами. Дополнительные сведения из спектрального анализа функции

приведены в п. 6.3.7.

6.3.4. Интегрирование и дифференцирование тригонометрических рядов Фурье

Пусть функция f (x) непрерывна или кусочно-непрерывна на [−l, l]. В силу замкнутости основной тригонометрической системы

в классе кусочно-непрерывных функций выполняется уравнение замкнутости (6.17), которое для тригонометрической системы можно записать в виде

(a0)2	∞	an2	+ bn2	=	1	l	(6.28)
2	+ n=1				l	Z−l f 2(x)dx.
	X

144

∞∞

XX

Из (6.28) следует, что ряды

an2 и

bn2 , где an и bn коэффици-

n=1 n=1

енты тригонометрического ряда Фурье любой кусочно-непрерывной функции f (x), сходятся. Из сходимости этих рядов следует, что

1

l

nπx

lim a

=

lim

Z−l f (x) cos

dx = 0,

n→∞

n

n→∞ l

l

l

lim b

=

lim

1

f (x) sin

nπx

dx = 0,

n→∞

n

n→∞ l

Z−l

l

т.е. коэффициенты ряда Фурье кусочно-непрерывной функции при n → ∞ стремятся к нулю.

Запишем соотношение (6.28) для суммы f (x) + g(x) и разности f (x)−g(x) двух любых кусочно-непрерывных на [−l, l] функций. При

этом заметим, что при сложении функций их соответствующие коэффициенты Фурье складываются, а при вычитании вычитаются. Через an и bn, αn и βn обозначены коэффициенты Фурье по тригонометрической системе функций f (x) и g(x), соответственно. Считая функции f (x) и g(x) периодическими с периодом 2l или периодически продолженными с участка [−l, l] на всю числовую ось, можно

записать

(a

0

+ α

)2

∞

(an + αn)2

+ (bn + βn)2

=

1

Z0

2l

2 0

+ n=1

l

[f (x) + g(x)]2dx,

X

(a0 − α0)2

+ ∞

(a

α

)2

+ (b

n −

β

)2

=

1

Z0

2l[f (x)

−

g(x)]2dx.

l

2

n=1

n −

n

n

X

Вычитая эти равенства (и сокращая на 4), получаем
a		α		∞	1	Z0	2l	(6.29)
		02	0 + n=1(anαn + bnβn) =		l		f (x)g(x)dx.
				X

Последнее равенство называют обобщённым уравнением замкнутости тригонометрической системы в классе кусочно-непрерывных

функций.

Теорема 6.3. Тригонометрический ряд Фурье кусочно-непрерыв- ной функции f (x) можно интегрировать почленно независимо от ха-

рактера его сходимости.

Доказательство. Пусть f (x) кусочно-непрерывна на [−l, l], пери-

одически продолжена на всю ось и

f (x)	a0	∞	nπx	+ bn sin	nπx	.	(6.30)
	2	+ n=1 an cos	l		l
		X

145

Запишем обобщённое уравнение замкнутости (6.29) для функции

f (x) и функции g(x), заданной в виде g(x) =	0, если	x0≤< x≤< 2l.
	1, если	0 x x0;

x0

Очевидно, α0 = 1l Z dx =

0

После сокращения на 1l

x0	2 dx +		∞		x0
					an cos
Z	a0				Z
			n=1
0			X		0

1

x0

1

x0

x

Z0

nπx

Z0 sin

nπx

0

,

αn =

cos

dx, βn =

dx.

l

l

l

l

l

соотношение (6.29) приводится к виду

nπx

x0

nπx

x0

Z

dx

Z

dx +

bn sin

= f (x)dx. (6.31)

l

l

0

0

Последнее и означает возможность почленного интегрирования ряда Фурье. Теорема доказана.

Подчеркнём, что даже если в (6.30) нет равенства (т.е. соответствующий ряд расходится или сходится не к f (x)), всё равно равен-

ство (6.31) справедливо. Для произвольных функциональных рядов, как мы видели в п. 3.2.3, это свойство не выполняется.

Для почленного дифференцирования имеет место более слабая теорема.

Теорема 6.4. Пусть функция f (x) дифференцируема на [−l, l].

Ряд для производной f ′(x) может быть получен из ряда f (x) =

a0

+

∞

nπx

nπx

2

X

an cos

его почленным дифференцировани-

+ n=1

l

+ bn sin

l

ем:

∞

nπ

· bn cos

nπx

−

nπ

nπx

(6.32)

f ′(x) n=1

l

l

l an sin

l .

X

Теорему примем без доказательства.

Вопрос о сходимости ряда (6.32) остаётся открытым. Нужны дополнительные исследования.

6.3.5. О равномерной сходимости тригонометрических рядов Фурье

Теорема 6.5. Если непрерывная и кусочно-гладкая на [−l, l] функция f (x) имеет равные на концах отрезка значения, т.е. f (−l) = f (l),

то её тригонометрический ряд Фурье сходится равномерно на этом отрезке, причём S(x) = f (x) в каждой точке [−l, l].

Доказательство. По теореме 6.2 имеет место равенство

f (x) =	a0	∞	nπx	+ bn sin	nπx	.	(6.33)
	2	+ n=1 an cos	l		l
		X

146

∞

Этот ряд мажорируется рядом |a20| + X(|an|+|bn|). Для доказатель-

n=1

	∞
	X
ства теоремы достаточно доказать, что ряд	(|an| + |bn|) сходится.
	n=1

Обозначим через a′n и b′n коэффициенты Фурье функции f ′(x) и установим их связь с коэффициентами an и bn. Применяя интегри-

рование по частям, находим

an = l

l

l

f (x) = u

) =

l f (x) cos

dx = ( cos nπx dx = dv

1

Z−

nπx

l

1

l

nπx l

1

l

l

nπx

l

Z−l f ′(x) sin

· bn′ ;

= l f (x) nπ sin

l

−l −

l

· nπ

l

dx = −nπ

1

l

nπx

l

l

1

bn = l Z−l f (x) sin

nπx

· nπ

−l+

l

dx = − l f (x) cos l

1

l

l

nπx

l

·

Z−l f ′(x) cos

dx =

· an′ .

+

l

nπ

l

nπ

(Первое слагаемое обращается в нуль за счёт того, что f (−l) = f (l).)

Мы получили

a

n|

=

l

b′ ,

b

=

l

· |

a′ .

(6.34)

nπ

|

· | n| | n|

nπ

n|

∞

b′

∞

a′

Докажем, что ряды

X

n

X

n

и

сходятся. Используем элемен-

n=1

n

n=1

n

1

тарное неравенство AB ≤

(A2 + B2) (оно следует из того, что

2

(A − B)2 ≥ 0). Положим в этом неравенстве A = |an′ |,

1

. Тогда

B =

n

an′

1

1

∞

|2

сходится (см. п. 6.3.4) и

| n

| ≤ 2 |an′

|2 + n2 . Так как ряд n=1 |an′

∞

X

1

сходится ряд

X

, то из последнего неравенства и признака срав-

n=1

n2

∞

a′

нения (см. п. 3.1.4) следует сходимость ряда

X

|

n|

. Аналогично

n=1

n

∞

b′

можно доказать сходимость ряда

X

| n|

. Теперь из (6.34) следует

n=1

n

147

∞	∞	∞
X	X	X
сходимость рядов	|an| и	|bn|. Сходимость ряда (|an| + |bn|)
n=1	n=1	n=1

доказана. По признаку Вейерштрасса ряд (6.33) сходится на [−l, l]

равномерно. Теорема доказана.

Заметим, что если функцию f (x), удовлетворяющую теореме 6.5, продолжить на всю числовую ось с периодом 2l, то получится непре-

рывная на всей оси функция. Если функция периодическая периода 2l непрерывна на всей числовой оси, то, очевидно, для неё выполняется условие f (−l) = f (l). Функцию назовём кусочно-гладкой на всей числовой оси, если она является кусочно-гладкой на каждой ко-

нечной её части. Теорему 6.5 можно несколько переформулировать. Если периодическая функция f (x) с периодом 2l непрерывна и

кусочно-гладкая на всей числовой оси, то её тригонометрический ряд Фурье сходится к ней равномерно на всей числовой оси.

6.3.6. Скорость сходимости тригонометрического ряда Фурье

Теорема 6.6. Если периодическая функция f (x) с периодом 2l

является непрерывной на всей числовой оси вместе со своими производными до m-го порядка включительно (m ≥ 0), а (m + 1)-я

производная кусочно-непрерывна, то порядок малости относительно n1 при n → ∞ коэффициентов Фурье an и bn этой функции по

тригонометрической системе не ниже m + 1, т.е. lim annm+1 = 0,
	n→∞
	∞
	X
nlim bnnm+1 = 0, при этом ряды	nν (|an| + |bn|), ν = 0, 1, 2, . . . , m
→∞	n=1

сходятся. Отметим, что для m = 0 теорема уже доказана в про-

цессе доказательства теоремы 6.5. В общем случае доказательство опустим.

Как видим, скорость сходимости тригонометрического ряда Фурье зависит от степени гладкости функции.

Теперь мы можем ответить на вопрос о почленном дифференцировании тригонометрических рядов. В соответствии с теоремой 3.25 для почленного дифференцирования ряда достаточно, чтобы выполнялись условия теоремы 6.6 при m = 1.

6.3.7. Комплексная форма ряда Фурье

Для интегрируемых комплексных функций одного вещественного аргумента вводят понятие скалярного произведения следующим образом. Пусть даны две функции:

148

ϕ1(x) =	u1(x) +	iv1(x), ϕ2(x)	=	u2(x) + iv2(x),		интегри-
руемые	на [a, b].	Скалярным	произведением		этих	функ-
ций называется число, определяемое				равенством	(ϕ1, ϕ2) =

=

ab ϕ1(x)

dx, где

= u2(x) − iv2(x) функция, сопряжён-

ϕ2(x)

ϕ2(x)

R

2

2

(x). Вместо функции ϕ

(x) взята функция

ϕ

2

(x) для того,

ная с ϕ

чтобы норма функции

hR

i

1/2

hR

1

i

1/2

||ϕ(x)|| = ab ϕ(x)ϕ(x)dx

=

ab |ϕ(x)|2dx

была числом вещественным. Функции ϕ (x) и ϕ2(x) называются ортогональными на [a, b], если (ϕ1, ϕ2) = 0.

Часто применяется система функций

l

, . . .

(6.35)

exp −

l

, exp −

i(n

−l

, . . . , 1, exp

inπx

1)πx

iπx

бесконечная в "оба конца". Так как exp

inπx

, exp

ikπx

=

l

l

l

dx

=

= Z exp

i(n

−

k)πx

0,

если

n = k,

2l,

если

n =6 k,

то система (6.35)

l

−l

exp

inπx

2

ортогональна на (−l, l) и

= 2l. Предположим, что

l

на ( l, l) ряд по системе

(x) разлагается в равномерно сходящийся

интегрируемая функция f

−

(6.35), т.е.

+∞

ck exp

ikπx

.

(6.36)

f (x) = k=

l

X

−∞

Умножим скалярно обе части этого равенства на exp

inπx

. Полу-

l

l

dx = 2lcn

чим Z

f (x) exp −

inπx

, поскольку система (6.35) орто-

l

−l

гональна на (−l, l), а квадрат нормы каждой её функции равен 2l.

Следовательно,

cn = 2l Z			l	− l		dx.	(6.37)
			f (x) exp
	1			inπx

−l

Покажем, что ряд (6.36), коэффициенты которого вычислены по формулам (6.37), есть ряд Фурье функции f (x) по основной

149

тригонометрической системе. Действительно, из (6.37) находим

c0

= 2l

Z

l

2 ,

cn = 2l Z

l

f (x) exp −

l

dx =

f (x)dx =

1

a0

1

inπx

−l

−l

1

l

nπx

nπx

an − ibn

=

f (x)

cos

i sin

dx =

.

2l Z

−

l

h

l

i

2

−

l

an + ibn

Аналогично, c−n =

. Можем записать

2

+ n=1 cn exp

l

=

n=

cn exp

l

= n=

cn exp

l

+ c0

∞

inπx

−1

inπx

∞

inπx

X

X

X

−∞

∞

−∞

∞

=

=

a0

inπx

inπx

2 + n=1 c−n exp −

l

+ n=1 cn exp

l

X

X

∞

2

n=1

an

2

− l

2

l

2

= a0 +

X

+ ibn exp

inπx

+ an − ibn exp

inπx

= a0 +

+ n=1

2

exp

l

+ exp

−

l

an

+ 2

exp

−

l

−

∞

1

inπx

inπx

1

inπx

X

− exp

l

ibn =

2 + n=1

an cos

l

+ bn sin

l .

inπx

a0

∞

nπx

nπx

X

Мы пришли к тригонометрическому ряду Фурье. Если совершить преобразования в обратном порядке, то мы от тригонометрического ряда Фурье перейдём к ряду (6.36). Следовательно, (6.36) есть другая эквивалентная форма записи тригонометрического ряда Фурье.

Пример 6.4. Представить рядом Фурье в комплексной форме

функцию f (x), если f (x) =

0,

при −1 ≤ x < 0,

1,

при 0 ≤ x ≤ 1.

Решение. В данном случае l = 1, поэтому

1

1

−1

e−inπx 1

1

c

=

e−inπxdx =

=

einπ

1

=

2 Z

−

2inπ

−

n

2inπ

0

0

n

i =

0,

(−1) − 1

−i

если n чётно;

=

,

если n нечётно.

Функция f (x) раз-

2nπ

π(2m + 1)

+∞

i

inπx

X

ложима в ряд Фурье, следовательно, f (x) = − n=−∞ π(2n + 1) e .

150