1490-spectry_i_analiz

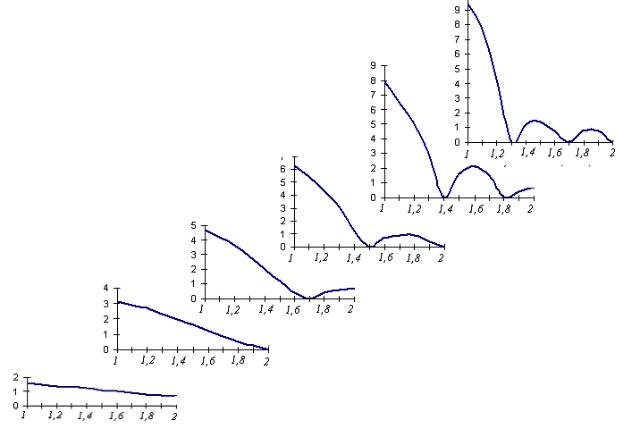
рис. 2.13 в виде последовательной серии функций спектральной плотности, отвечающих моментам времени nT / 2 (n =1, 2, 3, ...) . По горизонтальной оси для каждой из реализаций спектральной плотности отложено отношение частот ω/ Ω, а по оси ординат – спектральная плотность.

Рис. 2.13. Формирование текущего спектра синусоиды

Детали левого крыла спектральной плотности (ω/ Ω<1) опущены, что-

бы не усложнять рисунок. Из рис. 2.13 следует, что в начальной стадии формирования спектр является практически равномерным. Далее формируется максимум на частоте Ω. Затем начинается формирование боковых лепестков спектра, а максимум становится все более и более острым. Однако лишь в пределе при t →∞ спектральная плотность превратится в единственную спектральную линию, отвечающую бесконечно протяженному синусоидальному колебанию. При этом спектральная плотность на

82

частоте ω = Ω будет бесконечно велика и представляет собой так называемую δ – функцию, определенную в частотной области. В связи с этим необходимо проанализировать как процесс Фурье – преобразования сигналов, спектр которых в пределе превращается в δ – функцию, так и Фурье – преобразование сигналов, которые в пределе превращаются в δ – функции во временной области.

2.8. Преобразование Фурье δ – функции

Отметим прежде всего еще раз, что спектральное разложение функции времени x(t ), определяемое прямым преобразованием Фурье, существует только для функций, интегрируемых на интервале (−∞, ∞)

∞∫ x(t ) dt <∞

−∞

и удовлетворяющим условиям Дирихле, т.е. имеющим конечное число экстремумов на заданном интервале времени и конечное число разрывов первого рода на этом интервале.

Однако некоторые широко используемые в радиоэлектронике и связи сигналы не удовлетворяют условиям абсолютной интегрируемости и их прямое преобразование Фурье (спектральное разложение) определить трудно. В связи с этим в учебные пособия по теории сигналов обычно включают разделы, посвященные вопросам преобразования Фурье неинтегрируемых функций и включающие в себя изложение искусственно вводимых предельных переходов, которые обеспечивают существование преобразований Фурье некоторых неинтегрируемых функций. Но, поскольку в следующей главе настоящей книги будут рассмотрены методы спектрального представления неинтегрируемых функций с использованием преобразования Лапласа, то изложение искусственно построенных методов спек-

83

трального анализа неинтегрируемых функций не является необходимым. В связи с этим в заключение настоящей главы будет рассмотрен только вопрос о преобразовании Фурье δ – функции Дирака [14].

2.8.1. Краткая история импульсной функции

Рассмотрим математическую модель бесконечно короткого импульса с бесконечно большой амплитудой, расположенного в произвольной точке

t0 оси времени t
∞	для	t =t0	,	(2.52)
δ (t −t0 )=	для	t ≠ t0.
0

При этом площадь импульса равна единице

∞∫δ (t −t0 )dt =1.

−∞

Функцию δ (t ) называют дельта – функцией, единичным импульсом, а

также функцией Дирака, поскольку она впервые была предложена П.Дираком. Эта функция представляет собой мощное орудие современной математической физики. Однако, как отмечают исследователи, в теоретической математике эта функция встречалась и до того, как Дирак «официально» ввел её в использование [14].

Так, Эрмит, в своем известном труде «Курс анализа» писал о сингулярном интеграле, все элементы которого равны нулю за исключением единственного бесконечно большого элемента, соответствующего некоторому значению аргумента.

Способ, при помощи которого Коши независимо от Фурье нашел теорему об интеграле Фурье, был основан на использовании того же типа импульсной функции, что была указана Эрмитом.

Пуассон также самостоятельно доказал теорему Фурье, используя путь, аналогичный пути Коши. Кроме того, Пуассон предложил идею «фильтрующего свойства» дельта – функции, которое будет рассмотрено ниже.

84

Кроме Коши, Пуассона и Эрмита с импульсной функцией был знаком Кирхгоф, когда он модифицировал принцип Гюйгенса для волновой теории света. Позже сам Гельмгольц также использовал идею импульсной функции.

Еще позже импульсная функция сыграла свою роль в работах Оливера Хевисайда по его «символическому исчислению» (то, что ныне мы связываем, прежде всего, с преобразованием Лапласа). В одной из своих работ, связанной с фильтрующим свойством дельта – функции, Хевисайд писал: «…эта функция выделяет одно значение произвольной функции в силу своей импульсивности…».

Однако с тех пор, как Дирак в 1930 году ввел импульсную функцию в квантовую механику, она известна под названием «дельта – функция» Ди-

рака и обозначается δ (t ).

2.8.2.Фильтрующее свойство δ – функции. Функции, аппроксимирующие

δ– функцию. Преобразование Фурье δ – функции

Дельта – функция обладает весьма важным свойством, широко используемым в математике, физике и радиотехнике. Это свойство заключается в следующем: если имеется некоторая непрерывная функция времени x(t ),

то справедливо соотношение

∞∫ x(t )δ (t −t0 )dt = x(t0 ) ∞∫δ (t −t0 )dt =x(t0 ).		(2.53)
−∞	−∞

Выражение (2.53) понятно, если учесть, что, по определению, функция

δ (t −t0 ) равна нулю на всей оси времени, за исключением точки t =t0 . Это обстоятельство превращает интервал интегрирования в бесконечно малый,

включающий в себя точку t =t0 . На этом интервале функция x(t ) прини-

85

мает единственное постоянное значение x(t )= x(t0 ), которое может быть вынесено за знак интеграла.

Выражение (2.53) характеризует так называемое «фильтрующее» значение δ – функции, заключающееся в способности выделять значение произвольной функции времени в конкретный момент времени, соответствующий положению δ – функции на оси времени.

Преобразование Фурье δ – функции формально можно определить как

		X& (ω)= ∞∫δ (t −t0 )exp(− jωt )dt,	(2.54)
		−∞
откуда, используя фильтрующее свойство δ – функции, получим
		X& (ω)= exp(− jωt0 ).	(2.55)
Для случая	t0 = 0	соотношение (2.55) дает спектральную плотность		δ –
функции в	виде	X& (ω)=1. Таким образом спектральная	плотность	δ –

функции является равномерно распределенной по оси частот в интервале

(−∞, ∞) в случае, если эта функция расположена в точке t0 = 0 . Если же

δ – функция расположена в произвольной точке оси времени (т.е. является смещенной относительно начала координат), то из выражений (2.54) и (2.55) следует, что спектр этой функции определяется теоремой смещения для преобразования Фурье.

Дельта – функция во временной области может быть представлена об-

ратным преобразованием от её спектральной плотности X& (ω)≡δ (ω)=1:

δ (t )=	1	∞∫δ (ω)exp( jωt )dω =	1	∞∫exp( jωt )dω .	(2.56)
	2π −∞		2π −∞

Учитывая свойство дуальности преобразований Фурье (т.е. условие

взаимозаменяемости частоты ω и времени t ), можно записать
δ (ω)= ∞∫exp(− jωt )dt.	(2.57)
−∞

86

Выражение (2.57) позволяет определить спектральную плотность гармонического колебания (например cosω0t ), заданного на бесконечном ин-

тервале времени. Подставляя этот сигнал в прямое преобразование Фурье

и используя формулу cosω			t		= 0,5	exp(	jω		t )+ exp(− jω	0	t ) , получим
		0						0
		X& (ω)= ∞∫cos(ω0t)exp[− jωt]=
			−∞
	∞	exp − j (ω −ω			)t dt + 0,5		∞	exp − j (ω −ω			)t dt .
= 0,5	∫			0			∫			0
	−∞						−∞

Используя соотношение (2.57), последнее выражение можно записать в виде

X&	(		)	(		0 )		(		0 )
		ω		=π δ	ω −ω		+δ		ω +ω	.	(2.58)

Таким образом, гармоническому сигналу с конечной (единичной) амплитудой соответствует дискретный спектр, содержащий две спектральные линии, которые представляют собой δ - функции, расположенные симметрично относительно начала координат на частотах ±ω0 (см. рис. 2.14).

X (ω)

−ω0

ω0 ω

Рис. 2.14. Спектральная плотность бесконечно протяженного гармонического колебания

Как на этом рисунке, так и в дальнейшем, символ означает δ – функцию. Продемонстрируем теперь, что δ – функция может быть представлена как предел некоторой реальной функции, зависящей от параметра, при стремлении этого параметра к бесконечности. Рассмотрение проведем с использованием нескольких примеров.

87

Пример 1. Зададим функцию x(t ) в виде двусторонней экспоненты x(t )= 0,5αn exp(−αn t ),

где αn – параметр.

Спектральная плотность x(t ) является функцией параметра αn :

X&n (ω)= 0,5αn ∞∫exp(−αnt )exp(− jωt )dt =

−∞

= 0,5αn ∫0 exp (αn − jω)t dt + 0,5αn ∞∫exp −(αn + jω)t dt =

−∞

0

1

0

1

∞

= 0,5α

exp (α

− jω)t

−

exp −(α

+ jω)t

=

n

n

n

αn − jω

αn + jω

−∞

αn2

0

1

1

.

(2.59)

= 0,5αn

+

=

−

jω

αn

+

2

+

ω

2

αn

jω

αn

На рис. 2.15а и 2.15б изображены процессы изменения как функции

Рис. 2.15а. Процесс изменения функции x(t ) в зависимости от величины параметра αn

x(t ) так и её спектральной плотности X&n (ω) в зависимости от величины параметра αn . Нетрудно видеть, что с ростом этого параметра двусторон-

88

няя экспонента сужается, а её спектр расширяется и стремится к равномерному. В пределе при αn →∞ двусторонняя экспонента превращается в δ –

функцию, обладающую равномерным бесконечным спектром.

Рис. 2.15б. Процессы изменения спектральной плотности X&n (ω) функции x(t ) в зависимости от величины параметра αn

Пример 2. Зададим x(t ) в виде функции Гаусса (гауссоида)

x(t )= απn exp(−αn2t2 )

и определим её спектральную плотность

X&n (ω)=	αn	∞∫exp(−αn2t2 )exp(− jωt )dt =	αn	∞∫exp −(αn2t2 + jωt ) dt.
	π −∞		π −∞

Для вычисления интеграла дополним показатель подынтегрального выражения до полного квадрата и получим

	αn			2	∞
X&n (ω)=		exp	−	ω		exp −(αnt + jω/ 2αn )2	dt.
	π			2
				4αn	−∞∫
Далее, используя замену переменных αnt + jω/ 2αn , dt = dx /αn							и учитывая,
что значение интеграла Эйлера – Пуассона определяется как

89

∞∫exp(−x2 )dx = π ,

−∞

получим

X& (ω)= exp(−ω2 / 4αn2 ).

Рис. 2.16а. Процессы изменения гауссоиды в зависимости от величины параметра αn

Рис. 2.16б. Процесс изменения спектральной плотности гауссоиды в зависимости от величины параметра αn

На рис. 2.16,а и 2.16,б изображены процессы изменения гауссоиды и её спектральной плотности в зависимости от величины параметра αn . Не-

90

трудно видеть, что с ростом этого параметра гауссоида сужается, а её спектр расширяется и стремится к равномерному, как и для двусторонней экспоненты. В пределе при αn →∞ гауссоида превращается в δ – функ-

цию, обладающую равномерным бесконечным спектром.

91