4.3 Нечеткие отношения

Для практических задач большое значение имеет понятие нечеткого отношения. Пусть имеется набор универсальных множеств . Возьмем прямое (декартово) произведение этих множеств и некоторое множество принадлежностей (например, [0,1]). Тогда нечеткое -арное отношение определяется как нечеткое подмножество на , принимающее свои значения в [0,1]. В случае =2 нечетким отношением между множествами будет называться функция , которая ставит в соответствие каждой паре элементов , величину . Нечеткое отношение на записывается следующим образом

.

В случае, когда множества совпадают, нечеткое отношение называется нечетким отношением на .

Декартовым произведением нечетких множеств , где , называется нечеткое множество из декартова произведения универсальных множеств с функцией принадлежности .

Распространенными примерами бинарных нечетких отношений являются «много больше чем», «имеет сходство», «имеет отношение».

Введем нечеткое бинарное отношение, которое играет роль единице в композиции отношений, следующим образом

Примеры.

1) Пусть , . Нечеткое отношение может быть задано, к примеру, в виде таблицы (матрицы отношений).

Таблица 11

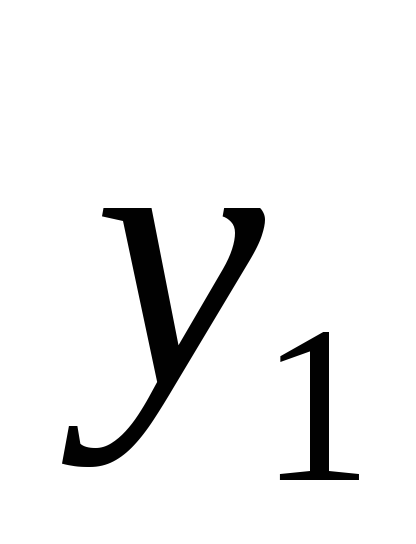
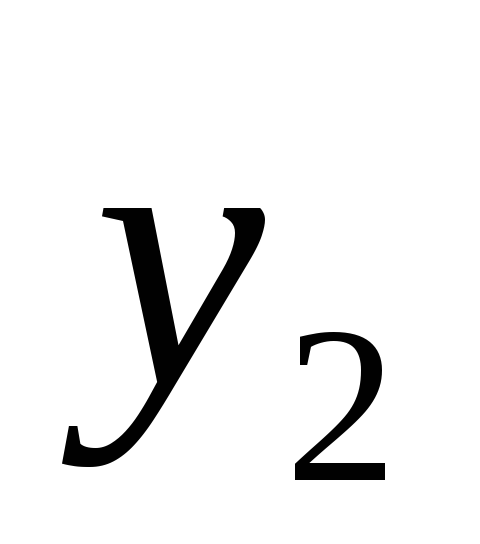
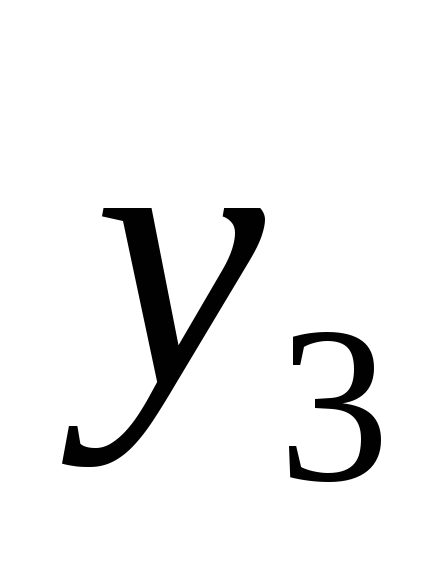
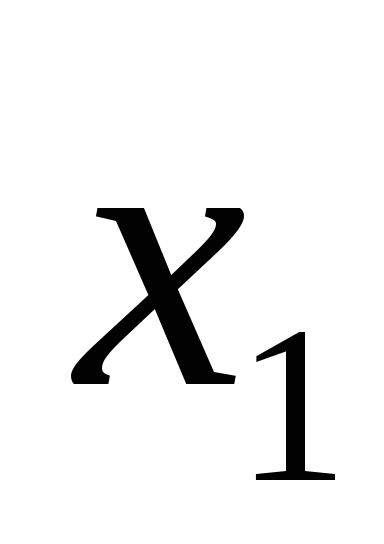
	0	0	O,1	0,3
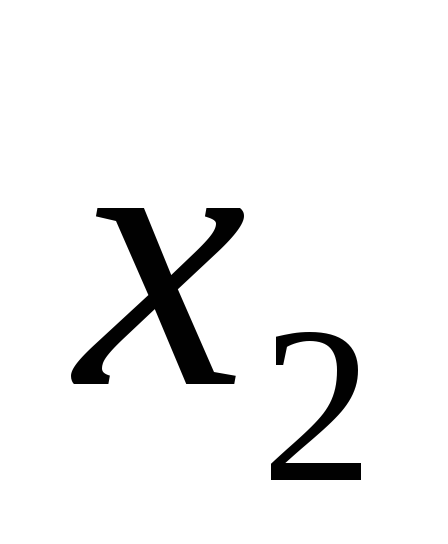
	0	0,8	1	0,7
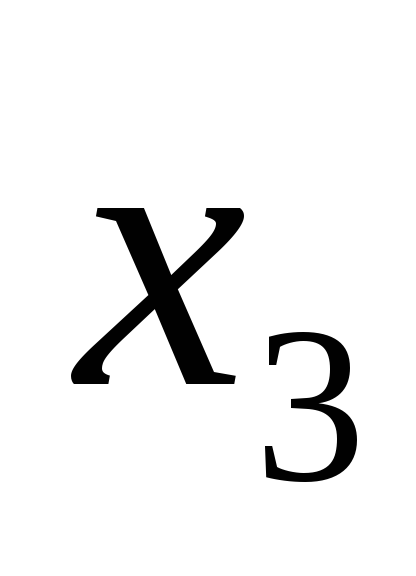
	1	0,5	0,6	1

Каждый элемент матрицы равен значению функции принадлежности для -ого значения и - ого значения .

2) Пусть , то есть множество всех действительных чисел. Отношение ( много больше ) можно задать функцией принадлежности

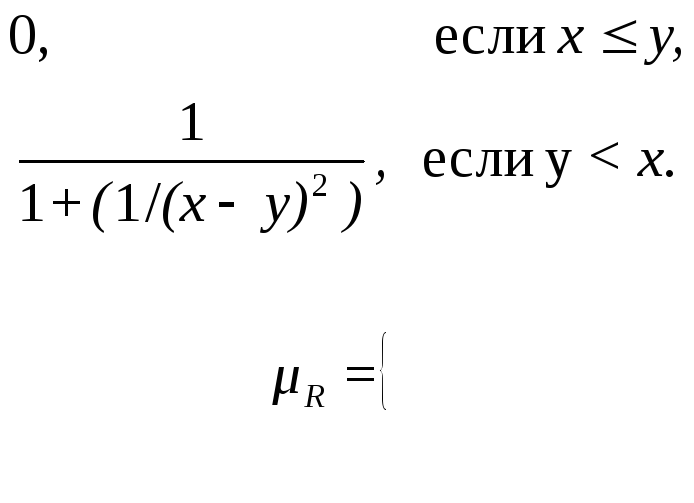
3) отношение , для которого

при достаточно больших можно интерпретировать так: «и близкие друг к другу числа».

4.4 Свойства нечетких отношений

Различные типы нечетких отношений определяются с помощью свойств, аналогичных свойствам обычных отношений, причем для нечетких отношений можно указать различные способы обобщения этих свойств.

1. Отношение на называется рефлексивным, если для любого элементасправедливо или, иначе, . Или можно записать как

, ,

2. Слабая рефлексивность

, ,

3. Сильная рефлексивность

, ,

4. Антирефлексивность

, ,

5. Слабая антирефлексивность

, ,

6. Сильная антирефлексивность

,

7. Симметричность

, , ,

8. Антисимметричность

, , ,

9. Асимметричность

, , ,

10. Сильная линейность

, , ,

11. Слабая нелинейность

, ,

12. Транзитивность

, , .

Операции над нечеткими отношениями

Объединение двух отношений . Объединение двух отношений обозначается и определяется выражением

.

Пересечение двух отношений . Пересечение двух отношений обозначается и определяется выражением

.

Алгебраическое произведение двух отношений . Алгебраическое произведение двух отношений обозначается и определяется выражением

.

Алгебраическая сумма двух отношений. Алгебраическая сумма двух отношений обозначается и определяется выражением

Для приведенных операций справедливы следующие свойства дистрибутивности:

,

,

,

,

,

.

Дополнение отношения. Дополнение отношения обозначается через и определяется выражением

.

Дизъюнктивная сумма двух отношений. Дизъюнктивная сумма двух отношений обозначается и определяется выражением

.

Обычное (четкое) отношение, ближайшее к нечеткому. Пусть - нечеткое отношение с функцией принадлежности . Четкое отношение, ближайшее к нечеткому, обозначается и определяется выражением

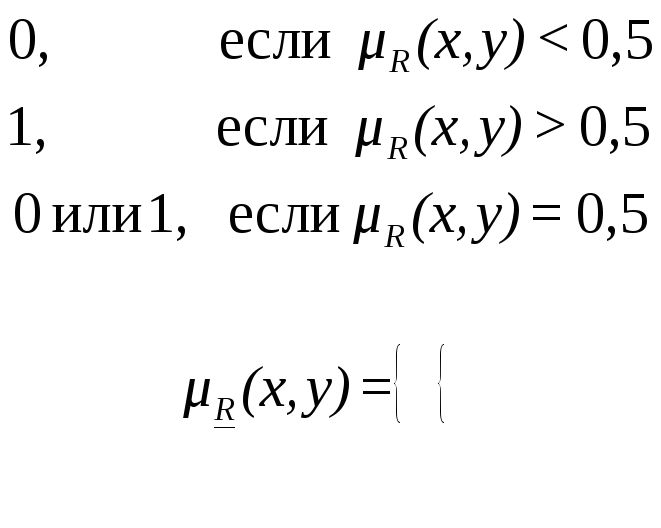
Обычно по договоренности принимают при .

Композиция (свертка) двух нечетких отношений. Пусть - нечеткое отношение между , и между . Нечеткое отношение между , обозначаемое через и, определяемое через выражением

,

Называется (max-min) – композицией ((max-min) – сверткой) отношений .

Пример. Пусть

	0,9	0	1	0,2
	0,3	0,6	0	0.9
	0,1	1	0	0,5

	0,1	0,7	0,4
	1	0,5	0

Тогда

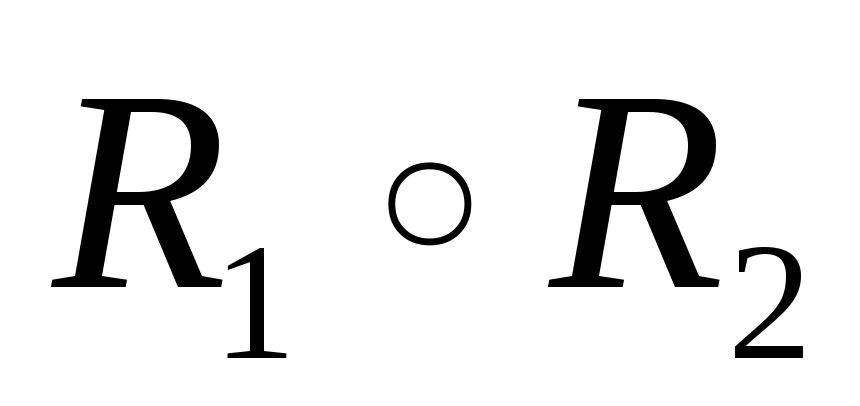
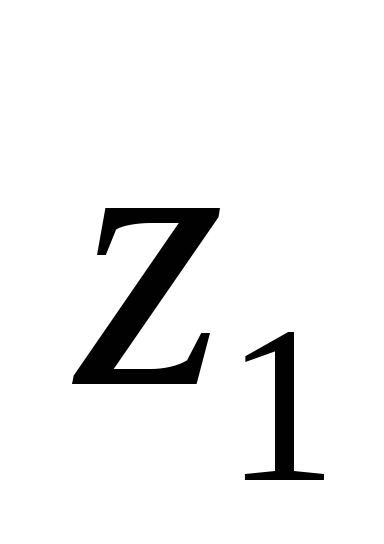
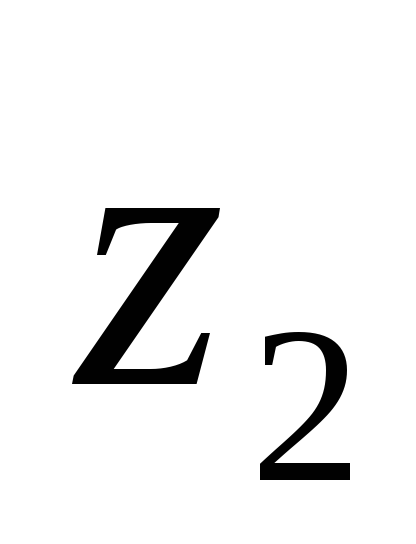
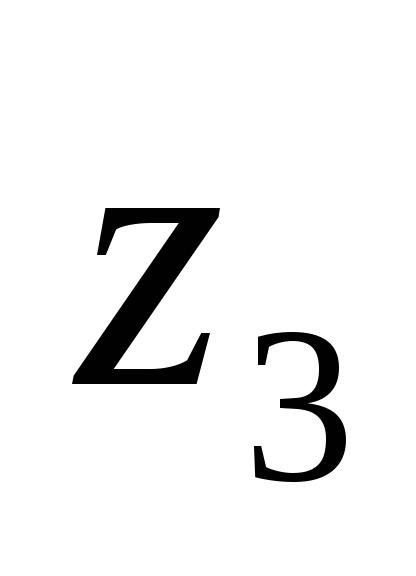
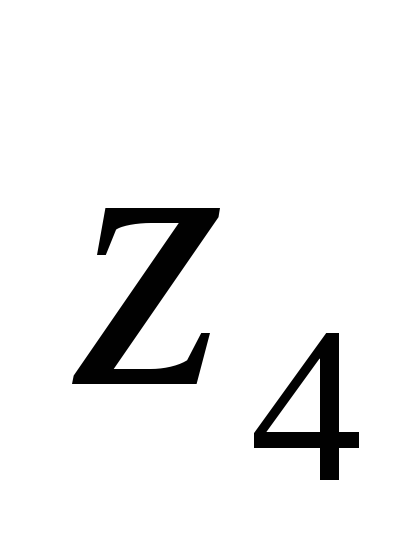
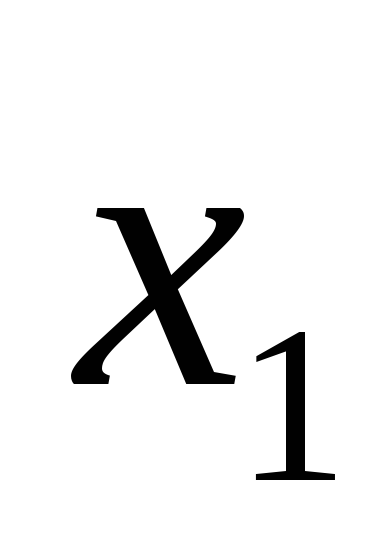
	0,3	0,6	0,1	0,7
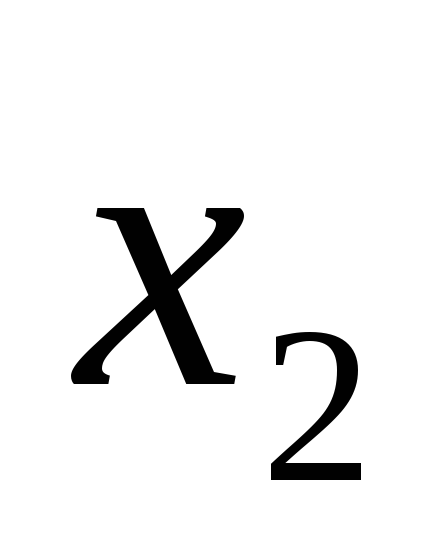
	0,9	0,5	1	0,5

Рассмотрим пример вычисления компонент матрицы при использовании (max-min) – композиции

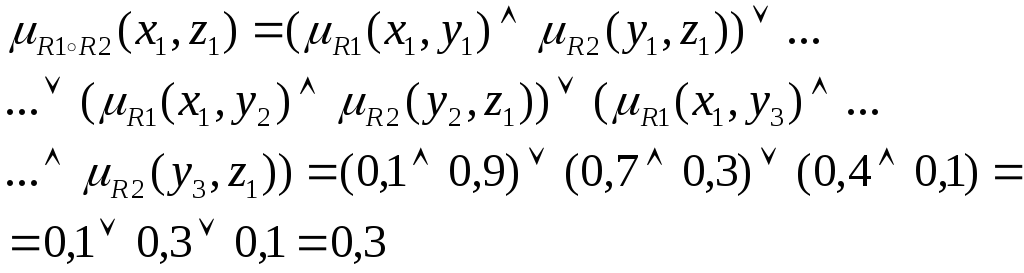
Подобным образом вычисляются и другие компоненты матрицы композиции. В данном примере использован «аналитический» метод вычисления композиции отношений , то есть -я строка «умножается» на -ый столбец с использованием операции , полученный результат «свертывается с использованием операции .

Свойства (max-min) – композиции. Операция max-min композиции ассоциативна, то есть

,

дистрибутивна относительно объединения, но недистрибутивна относительно пересечения

,

.

Кроме того, для max-min композиции выполняется следующее важное свойство: если , то .

Max – композиция. В выражении

Для max-min композиции отношений операцию можно заменить любой другой операцией, для которой выполняются те же ограничения, что и для : ассоциативность и монотонность (в смысле неубывания) по каждому аргументу. Тогда

.

В частности, операция может быть заменена алгебраическим умножением, в этом случае говорят о (max-prod) – композиции.

Декомпозиция нечетких отношений.

Одним из важнейших свойств нечетких отношений заключается в том, что они могут быть представлены в виде совокупности обычных отношений, причем могут быть упорядочены по включению, представляя собой иерархическую совокупность отношений. Разложение нечеткого отношения на совокупность обыкновенных отношений основано на понятии - уровня нечеткого отношения.

- уровнем нечеткого отношения называется обыкновенное отношение , определяемое для всех следующим образом

.

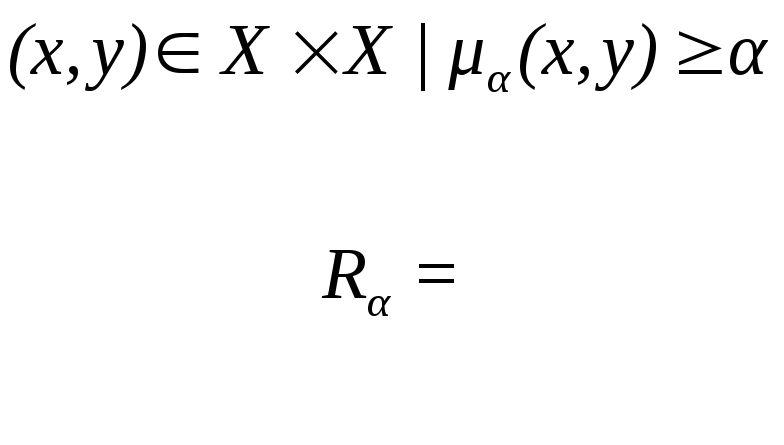Ясно, что - уровни удовлетворяют соотношению

,

представляя собой совокупность, вложенных друг в друга отношений.

Теорема. Нечеткое отношение обладает каким-либо свойствами из перечисленных (кроме сильной рефлексивности, сильной антирефлексивности, слабой линейности) тогда и только тогда, если этим свойством обладают все его - уровни.

Эта теорема играет важную роль в теории нечетких отношений. Во-первых, она показывает, что основные типы обычных отношений и их свойств могут быть обобщены и на случай нечетких отношений, и проводит ясный способ такого обобщения. Во-вторых, оказывается, что основные типы нечетких отношений могут быть представлены как совокупность, иерархия обычных отношений того же типа. И если решением практической задачи является получение на универсальном множестве некоторого отношения заданного типа, например, эквивалентности или порядка, то построение на универсальном множестве соответствующего нечеткого отношения позволяет получить сразу ансамбль необходимых обычных отношений, а это дает возможность учитывать неоднозначность решений, присущих практическим ситуациям, и предоставляет лицу, принимающего решение, некоторую свободу выбора. В-третьих, теория нечетких множеств, допуская неоднозначность решений, ограничений и целей, дает подобную неоднозначность возможных решений, ограничений и целей, дает возможность оперировать сразу всей совокупностью таких объектов как единым целым.

Нечеткое отношение , может быть представлено в следующем виде

=,

где определяется следующим образом

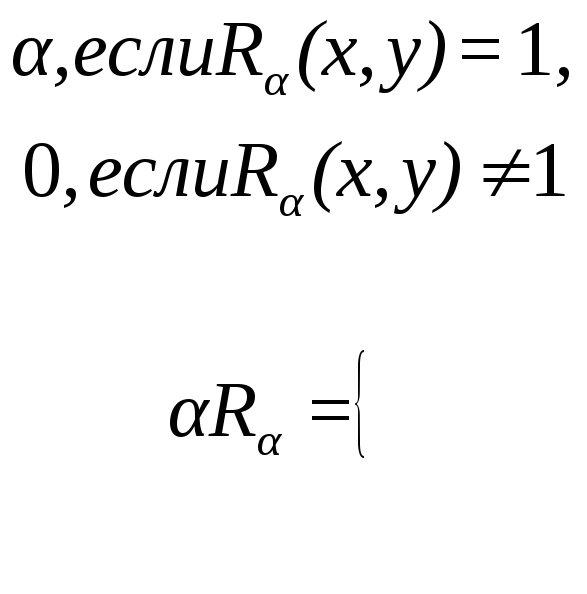
Кроме вышеописанных свойств, выполняющихся для всех - уровней, могут быть определены свойства, выполняющиеся только для одного или нескольких уровней. Примеры таких свойств, в предположении, что элемент фиксирован:

- симметричность

, .

- транзитивность

, .

Транзитивное замыкание нечетких отношений

Большое значение в приложения нечетких отношений играют транзитивные отношения. Они обладают многими удобными свойствами и определяют некоторую правильную структуру универсального множества. Например, если отношение характеризует сходство между объектами, то транзитивность такого отношения обеспечивает возможность разбиения универсального множества на непересекающиеся классы сходства. Если отношению в придавать смысл «предпочтения» или «доминирования», то транзитивность такого отношения обеспечивает возможность естественного упорядочения объектов универсального множества, существование «наилучших», «недоминируемых» объектов и т. п. Поэтому представляет большой интерес возможность преобразования исходного нетранзитивного отношения в транзитивное. Такое преобразование обеспечивает операция транзитивного замыкания нечеткого отношения.

Транзитивным замыкание отношения называется отношение , определяемое следующим образом:

где определяется рекурсивно:

,

Теорема. Транзитивное замыкание любого нечеткого отношения транзитивно и является наименьшим транзитивным отношением, включающим , то есть и для любого транзитивного отношения , такого, что , следует .

Как следствие из данной теоремы получаем, что транзитивно тогда и только тогда, если .

Если множество содержит элементов, то имеем

.

В случае, когда рефлексивно, имеем

.

Весьма важным фактором является то, что - уровень транзитивного замыкания нечеткого отношения совпадает с транзитивным замыканием соответствующего - уровненя:

для всех .

Следует отметить, что транзитивное замыкание нечеткого отношения в общем случае сохраняет лишь некоторые свойства отношения . Такими свойствами являются рефлексивность, симметричность, линейность и транзитивность.

Проекции отношений

Важную роль в теории нечетких множеств играет понятие проекции отношения. Дадим определение этому понятию для бинарного отношения. Пусть - нечеткое бинарное отношение между с функцией принадлежности .

Проекция отношения на универсальные множества и обозначается как и и представляет собой нечеткое множество в с функцией принадлежности

,

.

Пример 1. Пусть - числовая прямая и в задано нечеткое отношение с функцией принадлежности

.

Найдем проекции и . Поскольку функция принадлежности дифференцируема по обоим аргументам во всей плоскости, то для фиксированного значения из уравнения , что доставляет максимум функции принадлежности при любом произвольном фиксированном значении . Подставляя это значение в функцию принадлежности, получим проекцию нечеткого отношения на

.

Подобным образом, из решения уравнения при фиксированном , находится значение , которое доставляет максимум функции принадлежности. Подставляя значение в функцию принадлежности, определим вторую проекцию

.

Пример 2. Пусть на задана функция

.

Определим нечеткое отношение в с функцией принадлежности

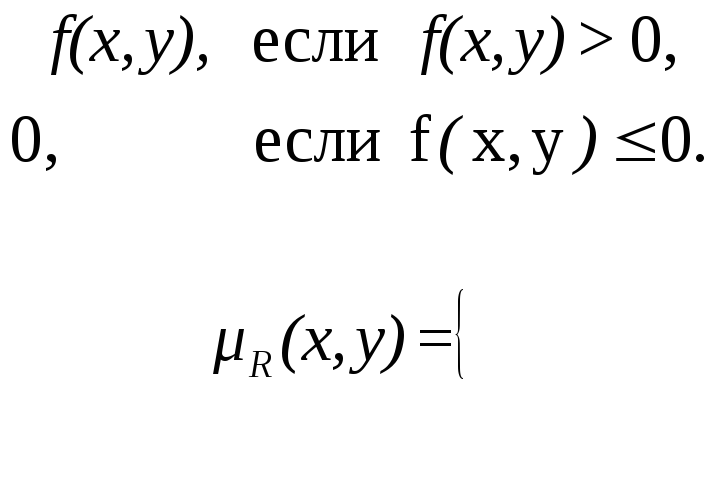
Из уравнения имеем и, следовательно,

Согласно определению, носитель нечеткого множества есть четкое множество из универсального множества, на котором . Следовательно, носитель нечеткой проекции на будет открытый интервал

.

Из уравнения имеем и, следовательно,

.

Условной проекцией первого типа нечеткого отношения на универсальное множество при произвольном фиксированном называется нечеткое множество с функцией принадлежности вида

Аналогично определяется условная проекция на при заданном

Из определения проекций следует, что обычные проекции не влияют на условные проекции. Теперь дадим определение, которое учитывает их взаимосвязь. Введем понятие условных проекций второго типа.

Условные проекции второго типа определяются следующим образом:

Если или , то полагаем, соответственно, что или .

Поскольку для всех выполняется и , то условные проекции второго типа и .

Кроме того, условные проекции первого типа содержатся в соответствующих проекциях второго типа.

Независимость проекций

Пусть - нечеткое бинарное отношение между с функцией принадлежности , а и его проекции на , соответственно. Множества и называются независимыми, если их декартово произведение равно

.

При этом рассматривается независимость двух типов. Независимость первого типа имеет место в том случае, когда декартово произведения рассматривается как пересечение двух множеств с функцией принадлежности

.

Независимость второго типа предполагает, что декартово произведение рассматривается как алгебраическое произведение

.

В противном случае проекции и являются зависимыми.

Независимости второго типа можно дать следующую интерпретацию. Соотношения , с учетом произвольности и перепишем в виде

,

.

Сравнивая эти выражения с выражением , получим. Что для независимости второго типа необходимо и достаточно выполнение условий:

и .

Пример. Пусть в определено нечеткое отношение с функцией принадлежности

где такие, что .

Из уравнения

получим, что

.

Подставляя полученное выражение в функцию принадлежности , получим выражение для проекции нечеткого отношения на универсальное множество

.

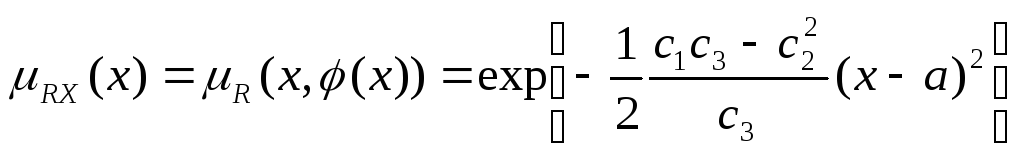Аналогично получим выражение для проекции на универсальное множество

.

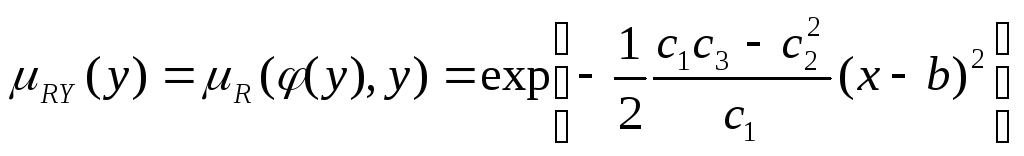Для условных проекций второго типа получим выражения:

,

.

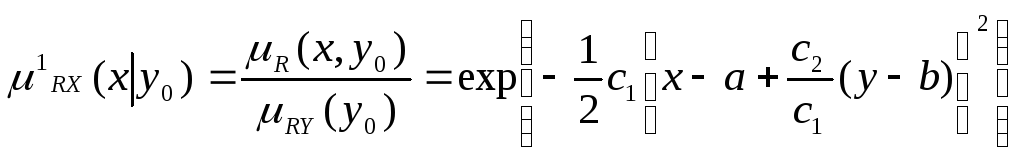Легко усмотреть, что если , то проекции и независимы по второму типу, поскольку в этом случае имеет место

и, кроме того, имеем

, .

Следовательно, при множества и являются независимыми по второму типу.

Если в исходном выражении для функции принадлежности положить, что , то получим

.

В этом случае имеет место

то есть проекции и являются независимыми по первому типу. Аналогичное утверждение имеет место при .

Теорема. Пусть - нечеткое бинарное отношение между с функцией принадлежности и существуют такие нечеткие множества, заданное на с функцией принадлежности и , заданное на с функцией принадлежности . Пусть имеет место .

Тогда, если имеет место равенство

,

то и являются проекциями бинарного нечеткого отношения .

Доказательство. Покажем, например, что . Для произвольного фиксированного имеем:

Теорема доказана для одной проекции . Для другой проекции доказательство проводится аналогично.

Теорема. Пусть - нечеткое бинарное отношение между с функцией принадлежности и существуют такие нечеткие множества, заданное на с функцией принадлежности и , заданное на с функцией принадлежности . Пусть множества и нормальные, то есть

,

а функция принадлежности бинарного отношения имеет вид

.

В этом случае нормальные множества и являются проекциями нечеткого отношения .

Доказательство. Покажем, например, что . Для произвольного фиксированного имеем:

Равенство доказывается аналогично.

Замечание. Из формул , легко можно вывести соотношения, аналогичные формулам Бейеса в теории вероятностей

,

.