5.8 Нечеткие высказывания и нечеткие выводы

Используемый в различного рода экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил. Нечеткой базой знаний называется совокупность нечетких правил «если – то», определяющих взаимосвязь между входами и выходами исследуемого объекта. Обобщенный формат нечетких правил такой:

П₁: если есть А₁, то есть В₁;

П₂: если есть А₂, то есть В₂;

……………………………………

П_n: если есть А_n, то есть В_n,

где - входная переменная (имя для известных значений данных), - переменная вывода (имя для значений данных, которое будет вычислено); A и B – функции принадлежности, определенные соответственно на и .

Пример подобного правила.

Если - низко, то - высоко.

Приведем более детальное пояснение. Знание эксперта отражает нечеткое причинное отношение предпосылки и заключения, поэтому его можно назвать нечетким отношением и обозначить через :

,

где «» называют нечеткой импликацией.

Отношение можно рассматривать как нечеткое подмножество прямого произведения полного множества предпосылок и заключений . Таким образом, процесс получения нечеткого результата вывода с использованием наблюдения и знаний можно представить в виде формулы

,

где «» - операция свертки.

Как операцию композиции, так и операцию импликации в алгебре нечетких множеств можно реализовать по-разному, при этом, естественно, будет разниться и итоговый получаемый результат. Но в любом случае общий логический вывод осуществляется за следующие четыре этапа.

1. Нечеткость (введение нечеткости, фаззификация, fuzzification). Функции принадлежности, определенные на входных переменных применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила.

2. Логический вывод. Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям каждого правила. Это приводит к одному нечеткому подмножеству, которое будет назначено каждой переменной вывода для каждого правила. В качестве правил логического вывода обычно используются только операции «min» или «prod» - умножение. В логическом выводе «min» функция принадлежности вывода отсекается по высоте, соответствующей вычислению степени истинности предпосылки правила (нечеткая логика «И»). В логическом выводе «prod» функция принадлежности вывода масштабируется при помощи вычисленной степени истинности предпосылки правила.

3. Композиция. Все нечеткие подмножества, назначенные к каждой переменной вывода (во всех правилах), объединяются вместе, чтобы формировать одно нечеткое подмножество для каждой переменной вывода. При подобном объединении обычно используются операции «max» или «sum» - сумма. При композиции «max» комбинированный вывод нечеткого подмножества конструируется как поточечный максимум по всем нечетким подмножествам (нечеткая логика «ИЛИ»). При композиции «sum» комбинированный вывод нечеткого подмножества конструируется как поточечная сумма по всем нечетким подмножествам, назначенным переменной вывода правилами логического вывода.

4. Дополнительный этап – дефаззификация (defuzzification) – приведение к четкости, используется, когда полезно преобразовать нечеткий набор выводов в четкое число.

Имеется большое количество методов приведения к четкости, рассмотрим некоторые из них. В теории нечетких множеств процедура дефаззификации аналогична нахождению точечных характеристик (математическое ожидание, мода, медиана) случайных величин в теории вероятностей. Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности, что пригодно только для одноэкстримальных функций принадлежности. Для многоэкстримальных функций принадлежности в Fuzzy Logic Toolbox запрограммированы такие методы дефаззификации:

Centroid – центр тяжести;

Bisector – медиана;

LOM (Largest of Maximums) – наибольший из максимумов;

SOM (Smallest of Maximums) – наименьший из максимумов;

MOM (Mean of Maximums) – центр максимумов.

Дефаззификация нечеткого множества по методу центра тяжести осуществляется по формуле

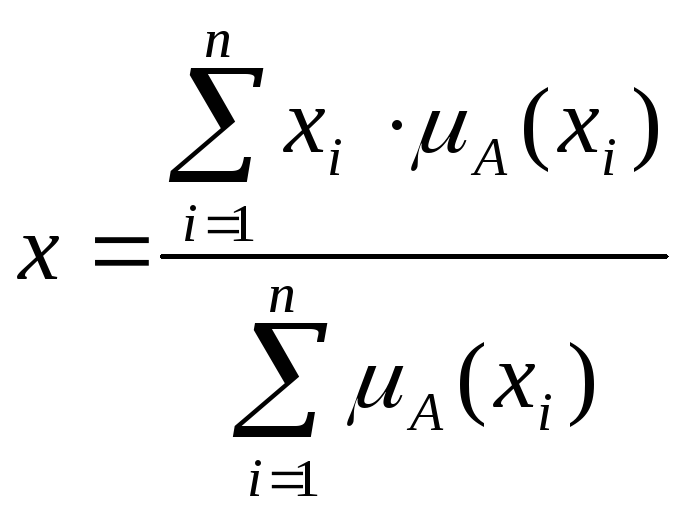
Дефаззификация нечеткого множества по методу медианы. Геометрической интерпретацией метода медианы является нахождение такой точки на оси абсцисс, что перпендикуляр, восстановленный из этой точки, делит площадь под кривой функции принадлежности на две равные части. Для дискретного множества дефаззификация осуществляется по формуле

и .

Дефаззификация нечеткого множества по методу центра максимумов. В методе центра максимумов находится среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежности. Если множество таких элементов дискретно и конечно, то формула дефаззификация по методу центра максимумов имеет вид

,

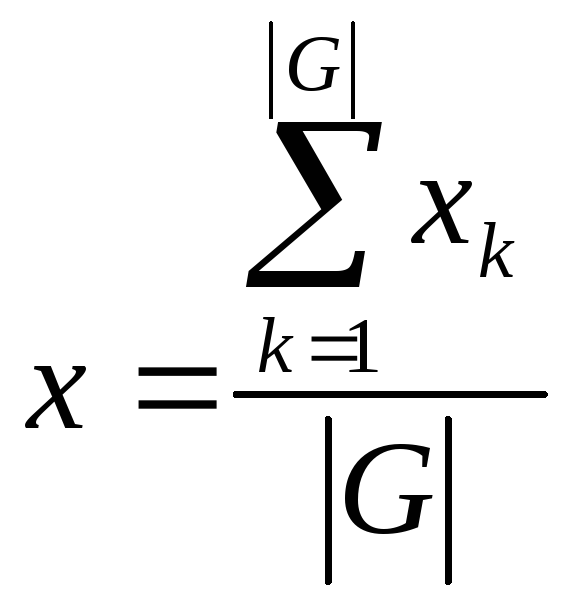где - мощность множества .

В дискретном случае дефаззификация по методам наибольшего и наименьшего из максимумов осуществляется по формулам и , соответственно.

Пример. Пусть некоторая система описывается следующими нечеткими правилами

П₁: если есть А, тогда w есть D;

П₂: если есть В, тогда w есть E;

П₃: если есть C, тогда w есть F.

где - имена входных переменных, - имя переменной выхода, а A, B, C, D, E, F – заданные функции принадлежности (обычно треугольной формы). Процедура логического вывода иллюстрируется на рис.6.

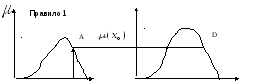
Рис.6. Иллюстрация к процедуре логического вывода.

В соответствии с приведенными этапами, на этапе 1 для данных значений и исходя из функций принадлежности A, B, C, находятся степени истинности для предпосылок каждого из трех приведенных правил.

На этапе 2 происходит отсекание функций принадлежности заключений правил, то есть D, E, F на уровнях .

На этапе 3 рассматриваются усеченные на втором этапе функции принадлежности, и производится их объединение с использованием операции max, в результате чего получается комбинированное нечеткое подмножество, описываемое функцией принадлежности и соответствующее логическому выводу для выходной переменной.

На 4 этапе (при необходимости) находится четкое значение выходной переменной, например, с применением центроидного метода: четкое значение выходной переменной определяется как центр тяжести для кривой

Рассмотрим пример, иллюстрирующий наиболее часто используемые модификации алгоритма нечеткого вывода, полагая, для простоты, что базу знаний организуют два нечетких правила вида:

П₁: если есть А₁ и есть В₁, тогда есть С₁;

П₂: если есть А₂ и есть В₂, тогда есть С₂,

где и - имена входных переменных, - имя переменной выхода, А, В, С – некоторые заданные функции принадлежности, при этом четкое значение ₀ необходимо определить на основе приведенной информации и четких значений ₀ и ₀. Иллюстрация к процедуре логического вывода приведена на рисунке 6.

1. Алгоритм Mamdani. Данный алгоритм соответствует рассмотренному примеру и рисунку 6. Математически его можно описать следующим образом.

1 этап (нечеткость). Находятся степени истинности для предпосылок каждого правила

.

2 этап (нечеткий вывод). Находятся уровни отсечения для предпосылок каждого правила с использованием операции min

,

,

затем находятся усеченные функции принадлежности для выходной переменной

,

.

3 этап (композиция). С помощью операции max производится объединение найденных усеченных, что приводит к получению итогового нечеткого подмножества для выходной переменной с функцией принадлежности

.

4 этап (приведение к четкости). Нахождение четкого значения можно провести, например, центроидным методом.

2. Метод Tsukamoto. Исходные посылки, такие же, как и у предыдущего алгоритма, но в данном случае предполагается, что функции принадлежности являются монотонными.

1 этап, такое же как в алгоритме Mamdani.

2 этап. Сначала, как и в алгоритме Mamdani, находятся уровни отсечения , а затем из решения уравнений

и

находятся четкие значения для каждого из исходных правил.

На 3 этапе определяется четкое значение выходной переменной, как среднее взвешенное

.

Пример. Пусть,, , , соответствующие уровни отсечения

,

Пусть в результате решения уравнений и найдены значения . Тогда четкое значение переменной вывода

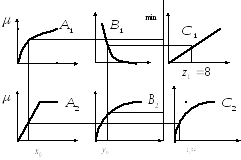
Рис 7. Иллюстрация к алгоритму Tsukamoto.

3. Алгоритм Sugeno.

Sugeno и Takagi использовали набор правил в следующей форме (пример двух

правил):

П₁: если есть А₁ и есть В₁, тогда ,

П₂: если есть А₂ и есть В₂, тогда .

Представление алгоритма.

1. Первый этап – как в алгоритме Mamdani.

2. На втором этапе находятся

,

и индивидуальные выходы правил

,

.

3. На третьем этапе определяется четкое значение переменной вывода

.

Рис. 8. Иллюстрация алгоритма Sugeno.

4. Алгоритм Larsen. В алгоритме Larsen нечеткая импликация моделируется с использованием операции умножения.

Описание алгоритма.

1. Первый этап – как в алгоритме Mamdani.

2. На втором этапе, как в алгоритме Mamdani вначале находится значения

,

,

а затем – частные нечеткие множества

и .

3. Находится итоговое нечеткое множество с функцией принадлежности

.

4. При необходимости производится приведение к четкости, как в ранее рассмотренных алгоритмах.

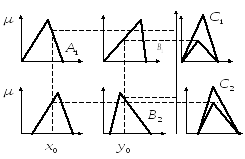
Рис. 9 Иллюстрация алгоритма Larsen.

5. Упрощенный алгоритм нечеткого вывода. Исходные правила задаются в данном случае в виде:

П₁: если есть А₁ и есть В₁, тогда ,

П₂: если есть А₂ и есть В₂, тогда ,

где - некоторые обычные четкие числа.

Описание алгоритма.

1. Первый этап – как в алгоритме Mamdani.

2. На втором этапе находятся числа

,

.

3. На третьем этапе находится четкое значение выходной переменной по формуле

.

Рис. 10 Иллюстрация упрощенного алгоритма.

6. Нисходящие нечеткие выводы.

До сих пор были рассмотрены нечеткие выводы, которые представляют собой восходящие выводы от предпосылок к заключению. В последнее время в диагностических системах начинают применяться нисходящие выводы. Рассмотрим механизм такого вывода на пример диагностики неисправности автомобиля с именами переменных:

- неисправность аккумулятора;

- отработка машинного масла;

- затруднения при запуске;

- ухудшение цвета выхлопных газов;

- недостаток мощности.

Между и существуют нечеткие причинные отношения , которые можно представить в виде некоторой матрицы с элементами . Конкретные входы (предпосылки) и выходы (заключения) можно рассматривать как нечеткие множества на пространствах . Отношения этих множеств можно представить как

,

где знак обозначает правило композиции нечетких выводов.

В данном случае направление выводов является обратным к направлению выводов для правил, то есть в случае диагностики имеется (задана) матрица (знания эксперта), наблюдаются выходы (или симптомы) и определяются входы (или факторы).

Пусть знания эксперта-автомеханика имеют вид

,

а результат осмотра автомобиля можно оценить как

.

Требуется определить причину такого состояния:

.

Отношение нечетких множеств можно представить в виде

.

Проведем транспонирование

.

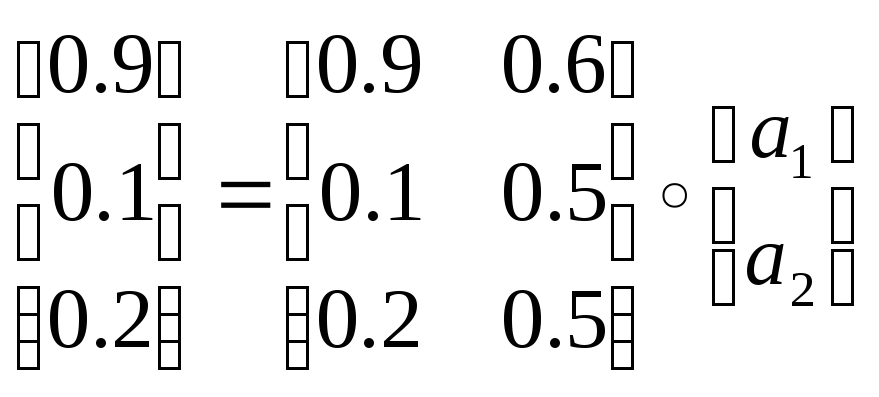При использовании (max-min) – композиции, получим

,

,

.

В первом уравнении второй член , как легко усмотреть, не влияет на правую часть, поэтому получим

,

следовательно, . Тогда из второго уравнения получим

, тогда

Полученное решение удовлетворяет третьему уравнению и, окончательно решение можно записать как

и .

Таким образом, лучше заменить аккумулятор ( - параметр неисправности аккумулятора, - параметр отработки машинного масла).

На практике в подобных задачах количество переменных может быть значительным, могут одновременно использоваться различные композиции нечетких выводов, сама схема может быть многокаскадной. Общих методов решения подобных задач в настоящее время, по-видимому, не существует.