
- •2008 Содержание
- •5.8 Нечеткие высказывания и нечеткие выводы… 112
- •6. Построение нечетких систем в диалоговом режиме с помощью Fuzzy Logic Toolbox ……….130
- •1 Обоснование теории нечетких множеств
- •1.1 Введение
- •1.2 Анализ видов неопределенности информации, характерных для процесса управления сложными системами
- •1.3 Человеко-машинные системы
- •1.4 Нечеткие системы
- •1.5 Возможности применения теории нечетких множеств и интервального анализа для описания различных видов неопределенности
- •2. Теория нечетких множеств
- •2.1. Четкие множества
- •2.2 Операции над четкими множествами
- •2.3 Декартово произведение множеств
- •3. Нечеткие множества
- •3.1 Понятие нечеткого множества
- •3.2 Некоторые характеристики нечетких множеств
- •3.3 Нечеткая и лингвистическая переменные
- •3.4 О методах построения функций принадлежности нечетких множеств
- •3.5 Операции над нечеткими множествами
- •4 Нечеткие числа
- •4.1 Понятие нечеткого числа
- •4.2 Операции над нечеткими числами
- •4.3 Нечеткие отношения
- •4.4 Свойства нечетких отношений
- •5 Основы математической логики
- •5.1 Алгебра высказываний
- •5.2 Булевы функции
- •5.3 Логика предикатов
- •5.4 Равносильные формулы логики предикатов
- •1) И ;
- •2) И ;
- •3) И ;
- •4) И .
- •5.5 Нечеткая логика
- •5.6 Нечеткие логические формулы и их свойства
- •5.7 Нечеткие предикаты и кванторы
- •5.8 Нечеткие высказывания и нечеткие выводы
- •5.9 Промышленные применения
- •6. Построение нечетких систем в
- •Диалоговом режиме с помощью
- •Fuzzy Logic Toolbox
- •1. Алгебра высказываний.
2.1. Четкие множества
Успехи современной математики в значительной мере принадлежит усилиям Аристотеля и философов, которые ему предшествовали. Их усилиями была создана четкая теория логики и позднее математики создали так называемые «Законы Мысли». Один из них – «Закон Исключения Середины», установил, что каждое суждение должно быть Истинно или Ложно, А или НЕ-А, это или не это. Каждое утверждение или предположение истинно или ложно или имеет значение 1 или 0. Следовательно, логику компьютера, который имеет дело с 1 и 0, называют четкой логикой, а обычные множества четкими множествами.
Введем основные термины и обозначения. Прописными буквами (например, X) будем обозначать совокупность объектов, с которыми будем иметь дело, а строчными буквами обозначим (например, x) – отдельные структурные элементы. Введем обозначение
![]() (2.1)
(2.1)
Фигурные
скобки означают совокупность объектов.
Совокупность объектов (здесь ![]() )
называется предметной областью или
универсальное (вспомогательное)
множество. Отдельные структурные
элементы назовем просто элементами или
объектами. Тот факт, что элемент x
принадлежит универсальному множеству
)
называется предметной областью или
универсальное (вспомогательное)
множество. Отдельные структурные
элементы назовем просто элементами или
объектами. Тот факт, что элемент x
принадлежит универсальному множеству
![]() ,
обозначается следующим образом
,
обозначается следующим образом
![]() (2.2)
(2.2)
Пусть
![]() универсальное множество,
универсальное множество, ![]() - некоторое свойство. Тогда четкое
подмножество множества
- некоторое свойство. Тогда четкое
подмножество множества ![]() ,
элементы которого удовлетворяют свойству
,
элементы которого удовлетворяют свойству
![]() ,
будем обозначать прописными буквами
,
будем обозначать прописными буквами
![]() .
Например, универсальное множество
состоит из десяти цифр
.
Например, универсальное множество
состоит из десяти цифр
![]() ,
(2.3)
,
(2.3)
![]() -
свойство быть четным. Тогда множество
-
свойство быть четным. Тогда множество
![]() - четные цифры будет
- четные цифры будет
![]() .
(2.4)
.
(2.4)
Число
структурных элементов определяет
мощность множества и называется
кардинальным числом. Для него вводится
обозначение ![]() ,
тогда в приведенных выше примерах
,
тогда в приведенных выше примерах
![]() ,
,
![]() (2.5)
(2.5)
Множества
с конечным кардинальным числом ![]() называются конечными и их можно записать
как в формулах (2.3) и (2.4), то есть перечислить
все его элементы. Если множество состоит
из одного элемента, то есть
называются конечными и их можно записать
как в формулах (2.3) и (2.4), то есть перечислить
все его элементы. Если множество состоит
из одного элемента, то есть ![]() ,
то такое множество называется синглетоном.
,
то такое множество называется синглетоном.
В случае бесконечных множеств, например, множество натуральных или вещественных чисел, этого сделать нельзя. В этом случае используется способ записи, при котором справа от вертикальной черты записываю свойство, которому удовлетворяют элементы множества. Например, формулу (2.4) можно записать в виде
![]() .
(2.6)
.
(2.6)
В общем случае можно записать
![]() .
.
Кроме того, для обозначения множества в виде рисунка часто используют диаграммы Венна. Они будут приведены ниже, когда речь пойдет об алгебраических операциях с множествами.
Помимо
приведенных способов задания четкого
множества, существует способ их
определения с помощью характеристической
функции. Характеристическая функция
![]() ,
определяющая множество
,
определяющая множество ![]() в универсальном множестве
в универсальном множестве![]() ,
представляет собой отображение, для
которого множество
,
представляет собой отображение, для
которого множество![]() есть область определения, а {0,1} (двузначное
множество из элементов 0 и 1) есть область
значений:
есть область определения, а {0,1} (двузначное
множество из элементов 0 и 1) есть область
значений:
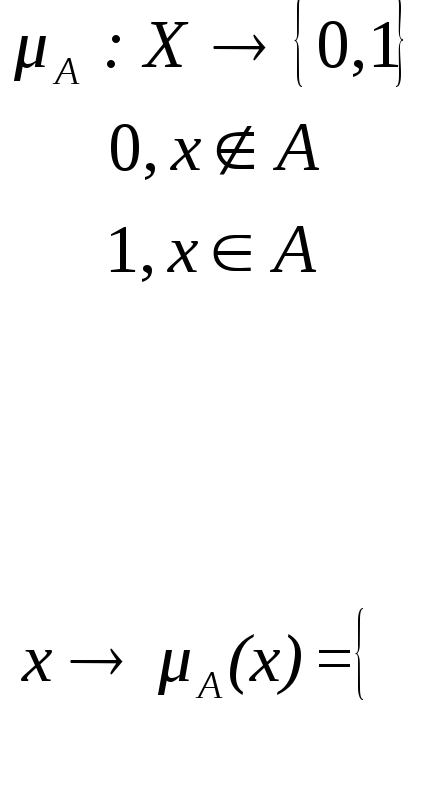 (2.7)
(2.7)
При
этом ![]() ,
если элемент
,
если элемент ![]() универсального множества
универсального множества ![]() ,
удовлетворяет свойству
,
удовлетворяет свойству ![]() множества
множества ![]() и
и ![]() ,
если не удовлетворяет. В универсальном
множестве
,
если не удовлетворяет. В универсальном
множестве ![]() можно рассматривать различные множества,
отвечающие различным свойствам
можно рассматривать различные множества,
отвечающие различным свойствам ![]() .
Объединение всевозможных множеств,
которые можно организовать из элементов
.
Объединение всевозможных множеств,
которые можно организовать из элементов
![]() и пустого множества называется степенным
множеством и обозначается как
и пустого множества называется степенным
множеством и обозначается как ![]() .
Например, пусть
.
Например, пусть
![]() (2.8)
(2.8)
Тогда степенное множество есть
![]() .
(2.9)
.
(2.9)
Вводится
понятие пустого множества, которое не
содержит ни одного элемента и обозначается
![]() .
Не следует путать пустое множество и
нулевой элемент. Множество, состоящее
из одного нулевого элемента, не является
пустым. Характеристическая функция
пустого множества есть
.
Не следует путать пустое множество и
нулевой элемент. Множество, состоящее
из одного нулевого элемента, не является
пустым. Характеристическая функция
пустого множества есть
![]() ,
для
,
для ![]() .
(2.10)
.
(2.10)
Здесь
![]() называется квантором всеобщности, его
можно читать словом «всех». Кроме того
есть квантор существования
называется квантором всеобщности, его
можно читать словом «всех». Кроме того
есть квантор существования ![]() в смысле «существует …».
в смысле «существует …».
В
отличии от пустого множества
характеристическая функция универсального
множества ![]() имеет вид
имеет вид
![]() ,
для
,
для ![]() .
(2.11)
.
(2.11)
